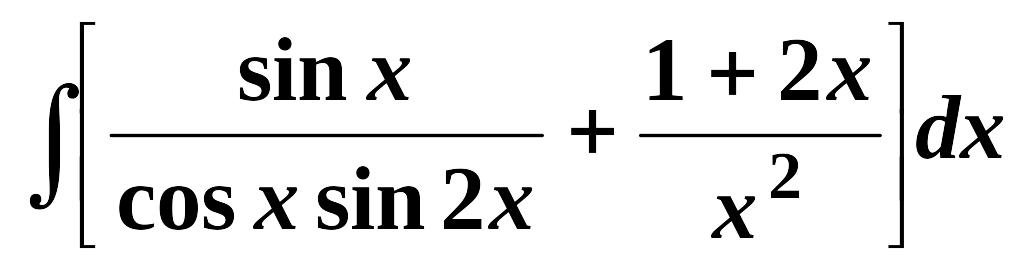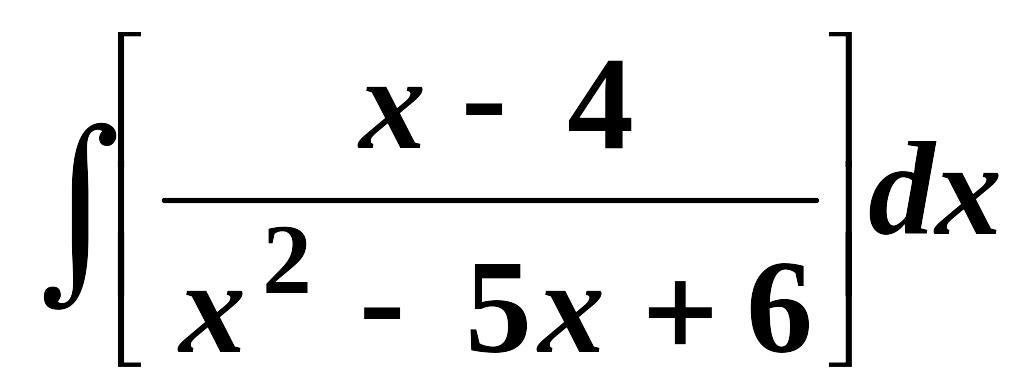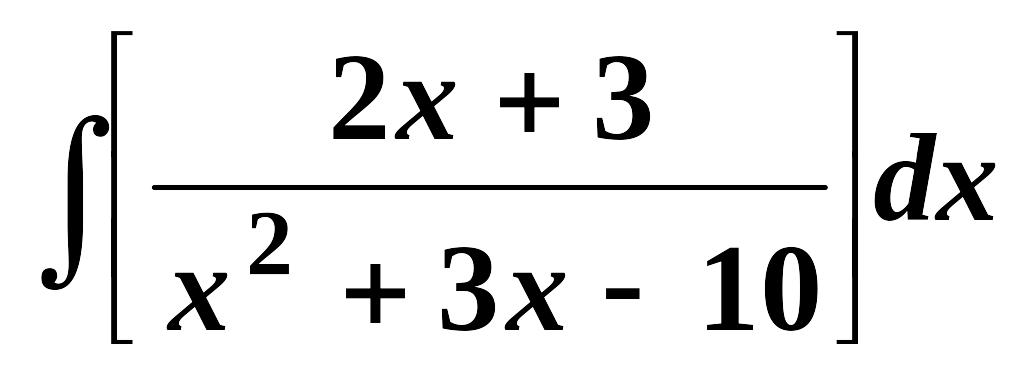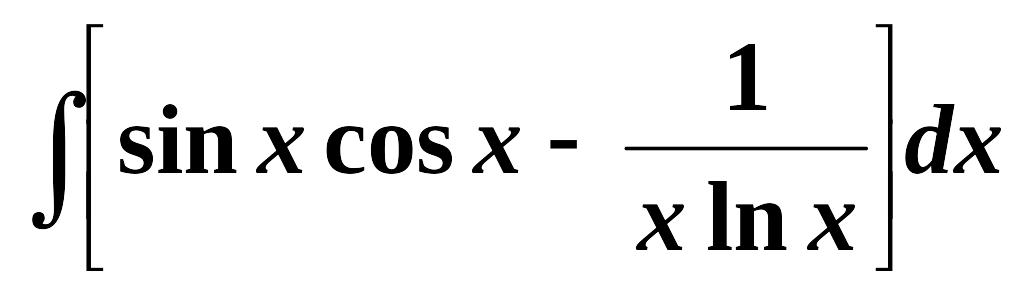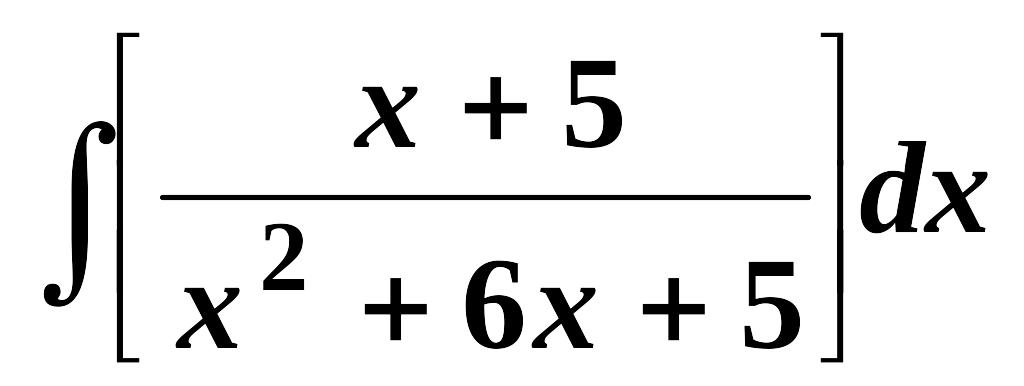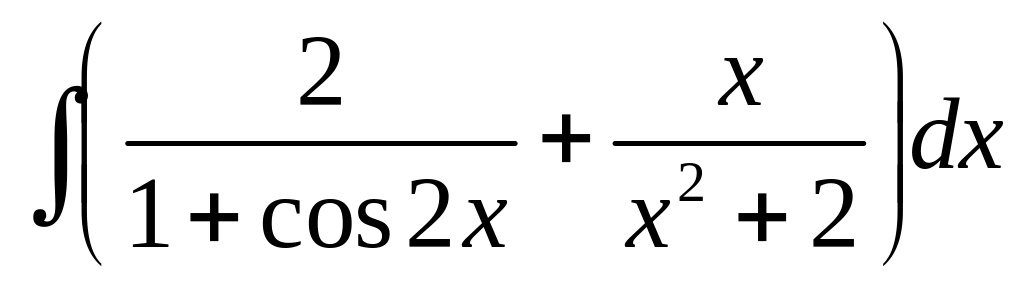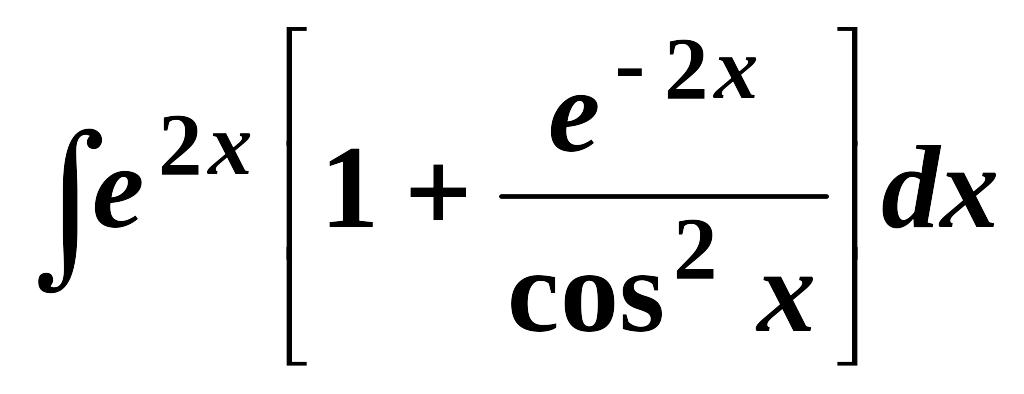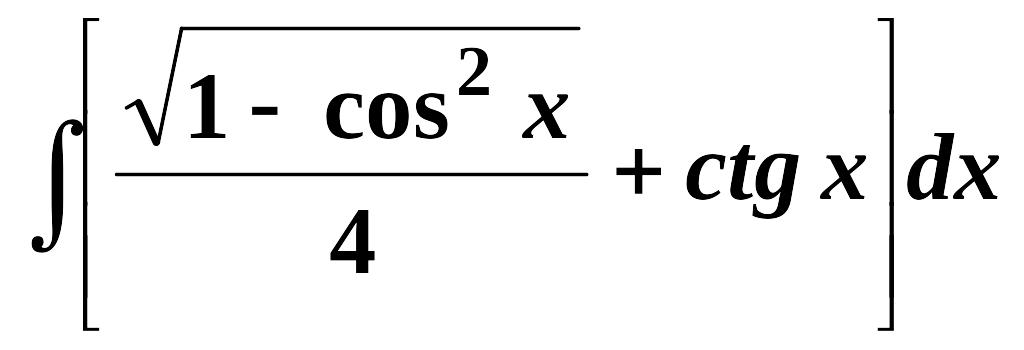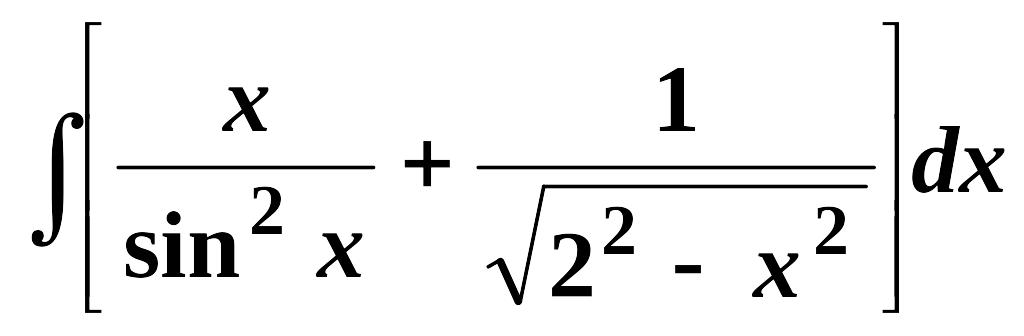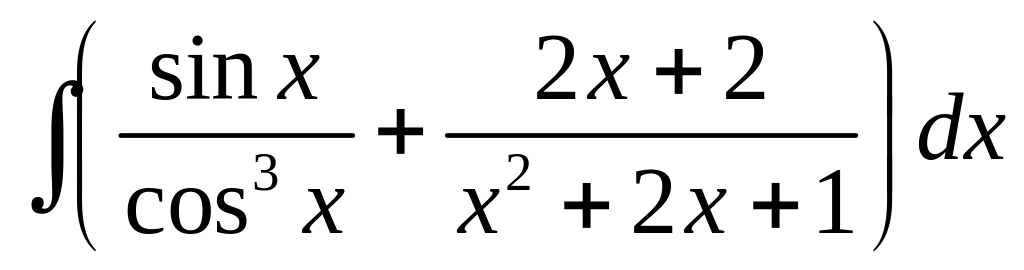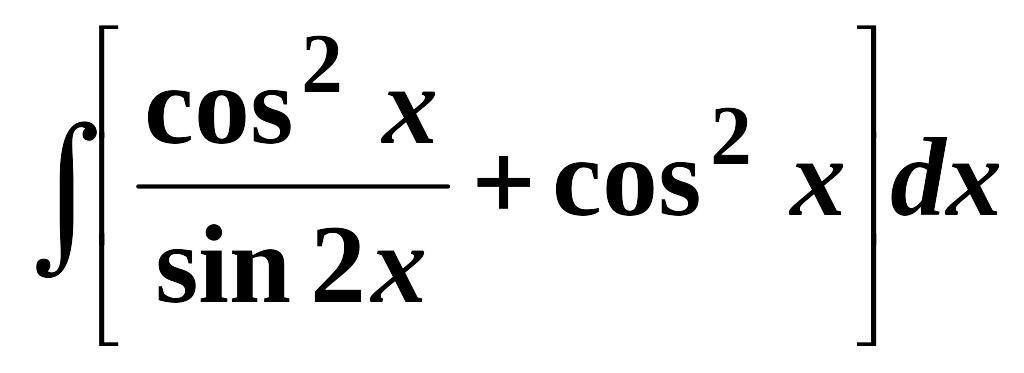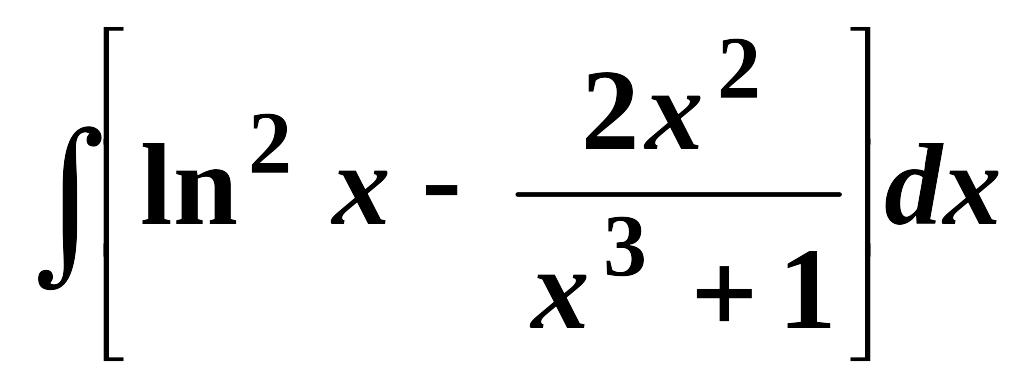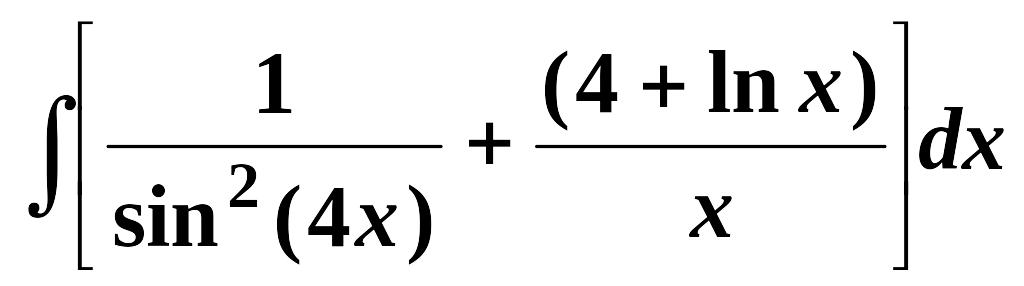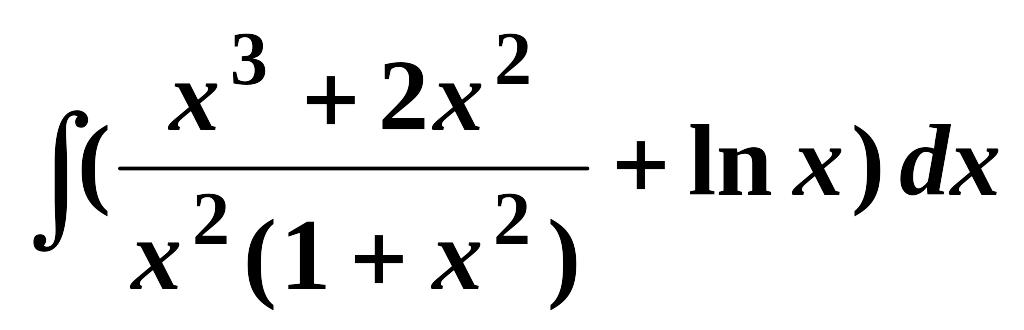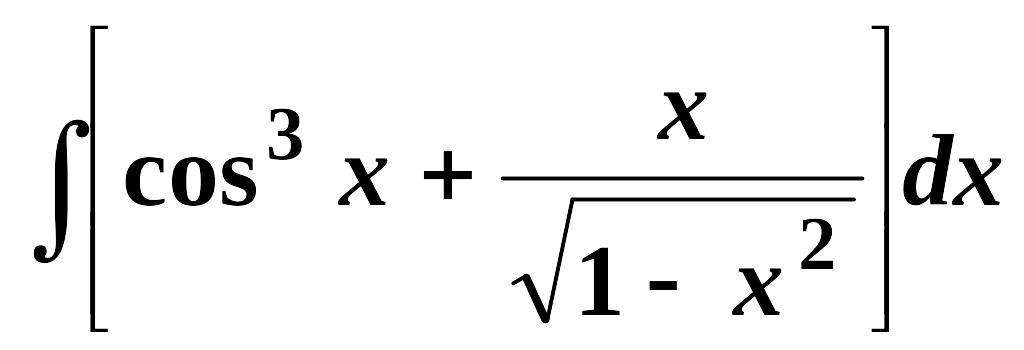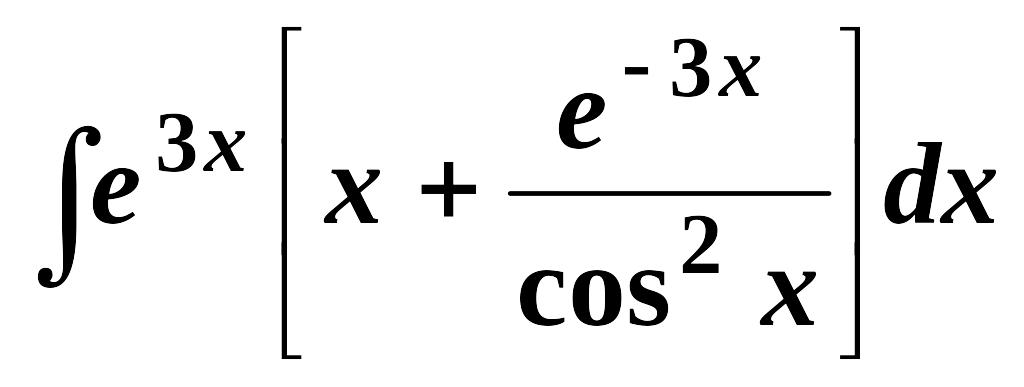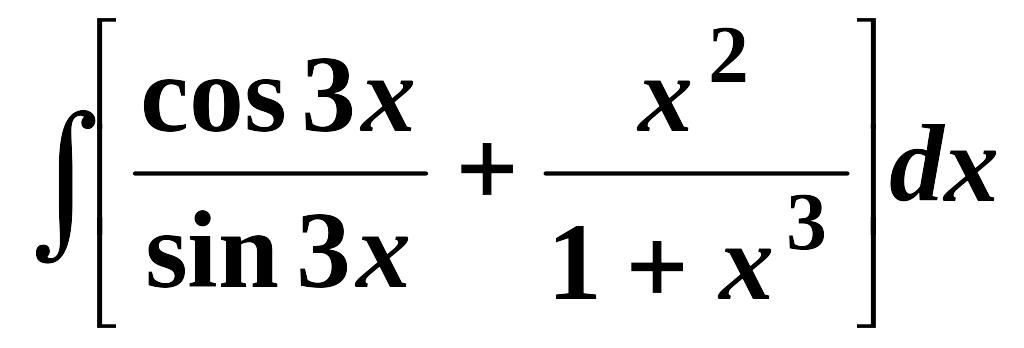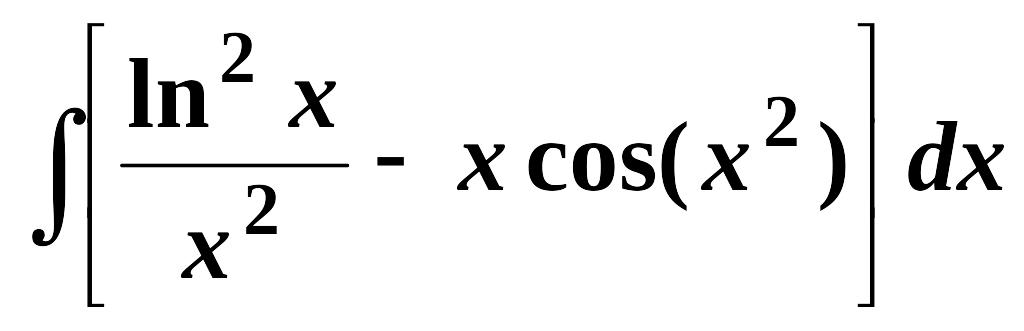4. Метод неопределенных коэффициентов
Применяется для интегрирования рациональных функций
,
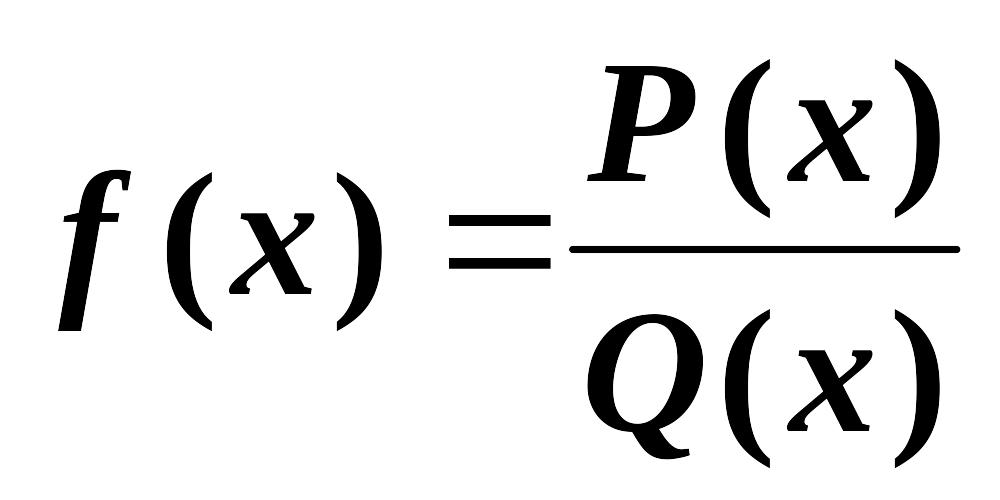где
и
– многочлены, и степень числителя меньше
степени знаменателя (правильная дробь),
неправильную дробь можно путем деления
многочлена на многочлен свести к сумме
некоторого многочлена и правильной
дроби.
По теореме из алгебры, всякий многочлен степени n со старшим коэффициентом, равным единице, имеющий действительные различные корни x1, x2, ..., xn, можно представить так:
Q(x)=( x – x1 )( x – x2)(x – xn ).
Тогда правильную дробь можно разложить на простейшие дроби и записать:
=
,
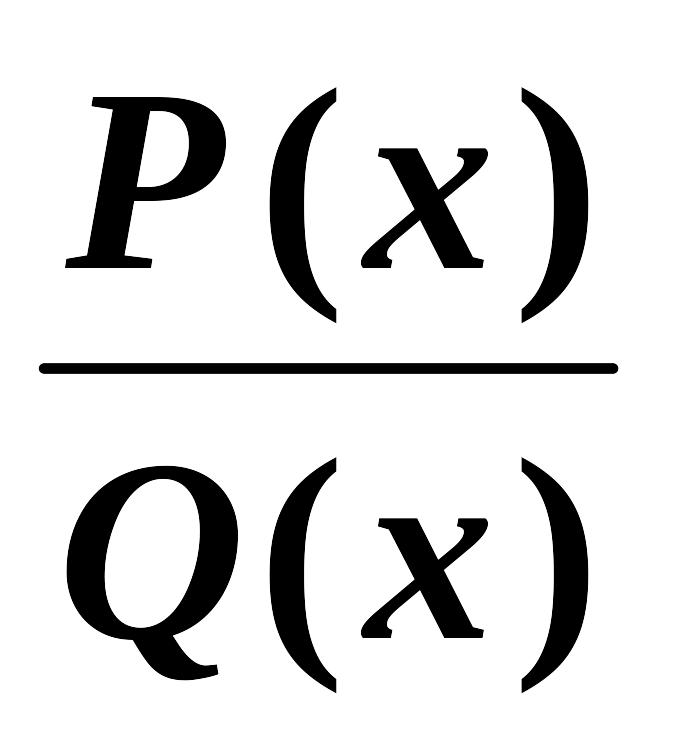где A1, A2, ..., An – некоторые числа (неопределенные коэффициенты).
Приведя правую часть выражения к общему знаменателю и приравняв затем коэффициенты при одинаковых степенях х в числителе левой и правой части, получим систему уравнений для определения неизвестных коэффициентов A1, A2, ..., An.
После этого интегрирование рациональной функции сводится к нахождению n интегралов вида:
.
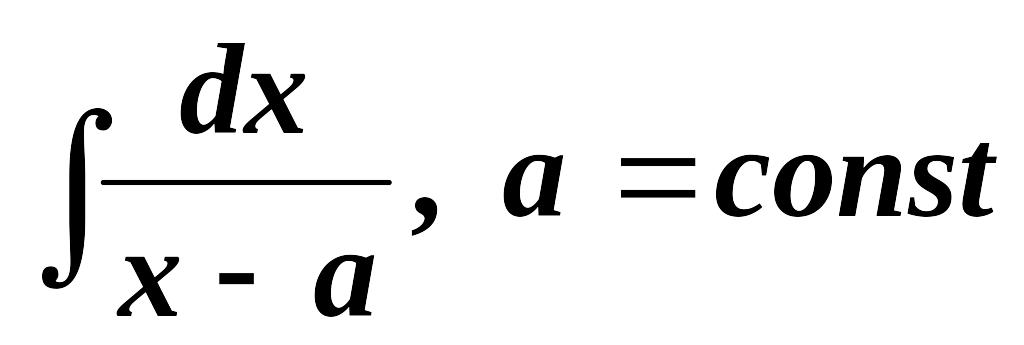Пример.
Найти интеграл
.
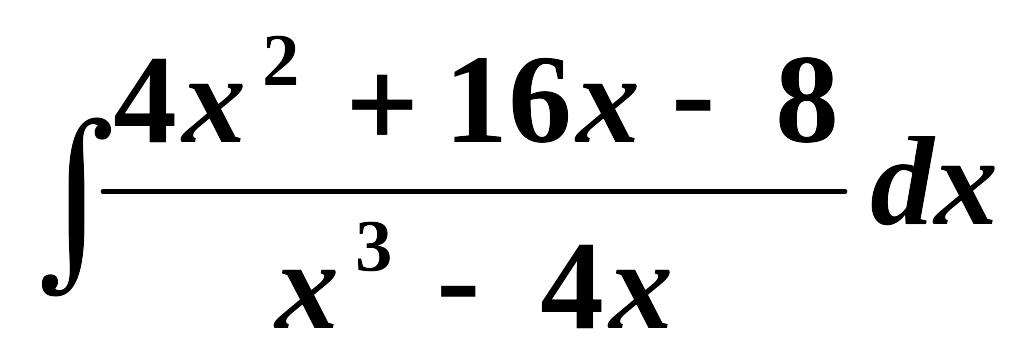Решение. Подынтегральная функция есть правильная дробь, разложим ее на простейшие дроби.
Знаменатель имеет вещественные, различные корни: x1 = 0, x2=2, x3= –2. Следовательно, x3–4x = x(x–2)(x+2) ,
.
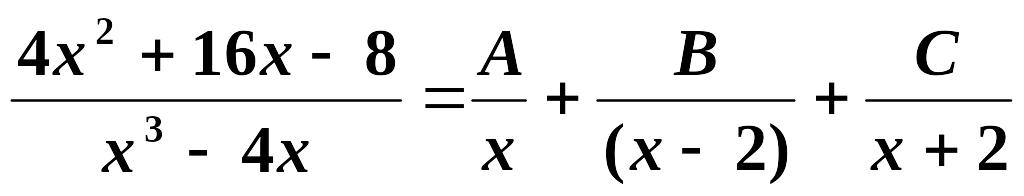Приведем правую часть последнего выражения к общему знаменателю и приравняем числители:
.
Приравниваем коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества:
отсюда определяем неопределенные коэффициенты разложения A, B, C:
A = 2, B = 5, C = – 3.
Следовательно,
=
=
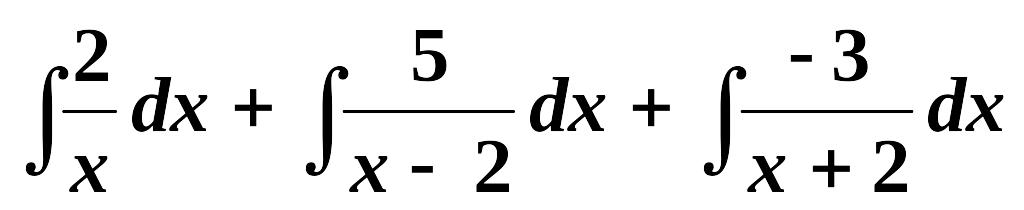= 2ln|x|+5ln|x–2|–3ln|x+2|+C =
.
Мы познакомились лишь с некоторыми наиболее часто используемыми приемами вычисления неопределенных интегралов, которые не охватывают всех случаев и не дают общих правил интегрирования. Кроме того, известны элементарные функции, для которых первообразная не является элементарной функцией (не выражается через простейшие функции с помощью конечного числа арифметических действий и суперпозиций).
Для таких функций интегрирование не может быть выполнено в конечном виде, т.е. в виде аналитической формулы, хотя ясно, что эти интегралы реально существуют. Интегралы, которые не выражаются через элементарные функции, называют “неберущимися”. На практике их вычисляют приближенными методами. Примеры “неберущихся” интегралов:
.
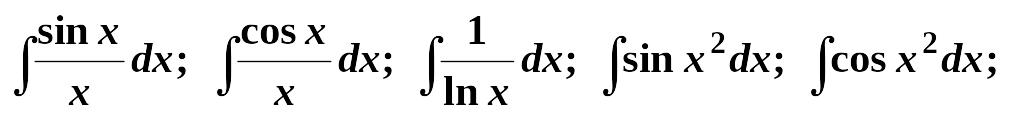
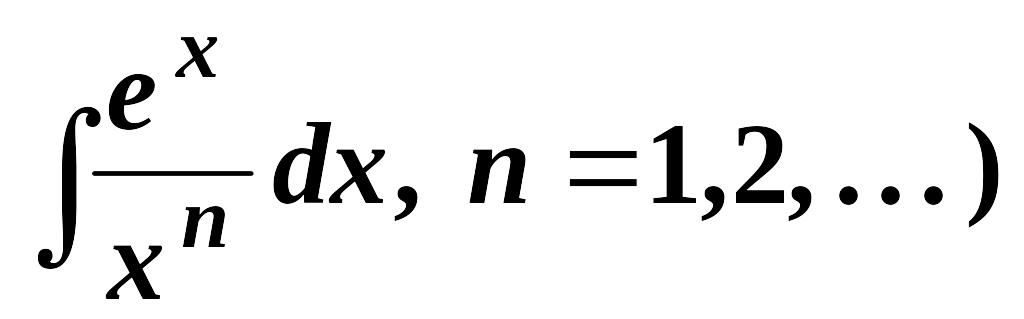Нет общих признаков, на основании которых можно было бы определить, берется ли данный интеграл в конечном виде.
Задание:. Повторить основные формулы тригонометрии:
;
;
;
;
;
;
;
;
;
;
.
Найти неопределенные интегралы (см. нижеприведенную таблицу):
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19.
|
20.
|
21.
|
