Лекция 11
3. Интегральное исчисление функции одного переменного
3.1 Первообразная функция и неопределенный интеграл
Умение вычислять производные позволяет решать ряд технических задач. Например, по заданному движению точки можно определить ее скорость и ускорение.
Движение точки задано, если задано ее положение по отношению к выбранной системе координат.
Положение точки в любой момент времени может быть определено, например, ее декартовыми координатами:
.
Тогда, вычислив производные от заданных функций по времени t, определим проекции вектора скорости на оси координат:
.
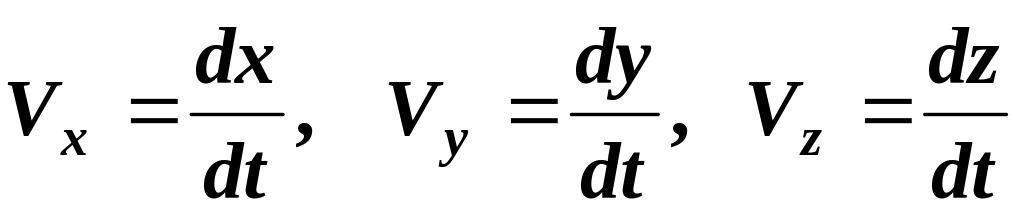По найденным проекциям легко найти модуль и направление вектора скорости:
,
.
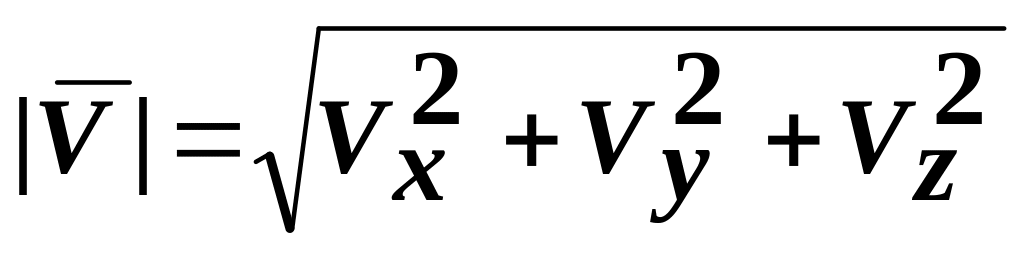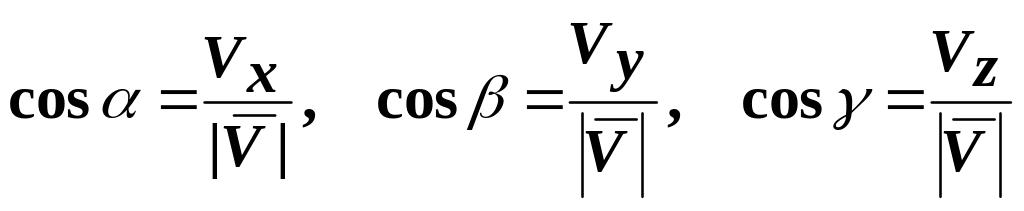Здесь a, b, g – углы, которые вектор скорости образует с осями координат.
Проекции вектора ускорения точки на оси координат равны производным от проекций скоростей или вторым производным от соответствующих координат точки по времени:
.
В практических задачах часто возникает необходимость по известному ускорению точки
найти ее скорость
,
или по известной скорости найти закон движения точки
.
Другими словами:
по известной производной нужно восстановить первообразную функцию, то есть решить задачу, обратную задаче дифференцирования.
Отыскание первообразных функций называют операцией интегрирования.
Задачи, связанные с интегрированием функций, рассматриваются в разделе математического анализа “Интегральное исчисление”.
Методы интегрального исчисления позволяют решать многие технические задачи: находить законы движения тел, работу сил и моментов, площади плоских фигур, длины дуг, площади поверхностей тел, объемы тел и другие задачи.
Интегральное исчисление применяется в решении ряда экономических задач для отыскания, например, опримального варианта деятельности предприятия при изучении влияния различных факторов на конечный результат. При этом экономические процессы описывают с помощью математических моделей, например, функциональных зависимостей.
Определение. Пусть на некотором промежутке Х задана непрерывная функция f(x).
Функция
F(x),
определенная на этом же промежутке,
называется первообразной для f(x)
, если
для
выполняются равенства:
(1)
(2)
Пример. Найти первообразную для функции
f(x)=2ax, а=const ≠ 0
Решение.
Простым подбором можно найти F(x)=ax2+C, где С – любая постоянная функция.
Проверка
Следовательно, можно предположить, что всякая непрерывная функция имеет множество первообразных, отличающихся постоянной С.
Теорема. Если функция f(x) имеет на промежутке Х первообразную F(x), то и все функции вида F(x)+C , где С – произвольная постоянная функция, будут для нее первообразными на том же промежутке.
Обратно, каждая функция Ф(х), первообразная для f(x) в промежутке Х, может быть представлена в форме Ф(х)= F(x)+C.
Доказательство. По определению первообразной, учитывая, что производная постоянной равна нулю, имеем:
,
Первое предложение теоремы доказано.
Пусть теперь
– любая
первообразная для
f(x)
в промежутке
Х:
.
Поскольку F(x) – тоже первообразная для f(x), то .
Так как функции Ф(х) и F(x) имеют одну и ту же производную, то они разнятся лишь на постоянную
Ф(х) = F(x)+C.
Теорема доказана.
Определение. Неопределенным интегралом от функции f(x) называется функция вида F(x)+C, которая имеет производную f(x) или дифференциал f(x)dx :
.
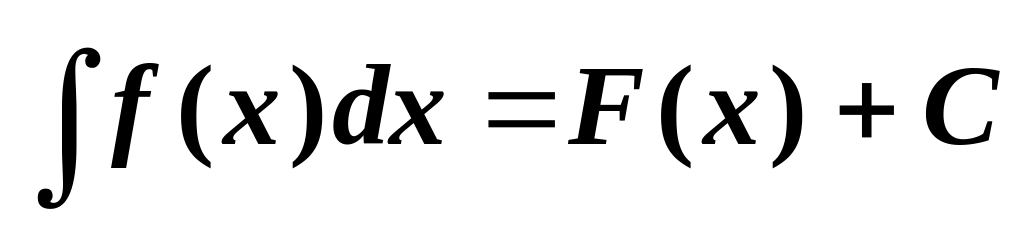Другими словами: Неопределенный интеграл от функции f(x) −это семейство её первообразных F(x)+C
f(x) называют подынтегральной функцией, переменную или выражение, стоящее под знаком дифференциала d, называют переменной интегрирования, выражение f(x)dx – подынтегральным выражением.
Сформулируем свойства неопределенного интеграла, вытекающие из его определения.