Лабораторная работа №2

“Определение коэффициента теплопроводности сыпучих материалов

методом шара”

Цель работы: углубление знаний в области теории теплопроводности и ознакомление с экспериментальным определением коэффициента теплопроводности сыпучих материалов. Коэффициент теплопроводности песка определяется методом шара на стационарном режиме.

1 Теоретические основы эксперимента

В общем случае дифференциальное уравнение теплопроводности имеет вид

, (1.1)

где t – температура,

qv – удельная производительность источников тепла, Вт/м,

c – теплоемкость вещества,

 - плотность вещества,

- коэффициент температуропроводности,

 - коэффициент теплопроводности.

Оператор Лапласа в сферической системе координат имеет вид

(1.2)

Для стационарного режима и при отсутствии внутренних источников тепла уравнение (1.1) примет более простой вид

, (1.3)

Или

(1.4)

Испытываемый материал расположен внутри шарового кольца, в центре которого размещен источник тепла – нагревательная спираль. С учетом изотропности испытываемого материала и равномерного распределения температуры по поверхности t_c1 и t_c2 и можно считать, что температура изменяется лишь в направлении радиуса.

Тогда дифференциальное уравнение теплопроводности примет вид

(1.5)

Граничные условия первого рода при

(1.6)

Проинтегрируем дважды уравнение (5):

(1.7)

Второе интегрирование

(1.8)

Определим постоянные интегрирования, воспользовавшись граничными условиями (1.6)

Из первого уравнения выразим постоянную и подставим во второе

Откуда

(1.9)

(1.10)

Подставим найденные значения постоянных (1.9) и (1.10) в уравнение (1.8) и получим

(1.11)

Количество тепла, проходящего через шаровую поверхность величиной F в единицу времени, связано с коэффициентом теплопроводности и градиентом температуры, известной как закон Фурье зависимостью

, (1.12)

где  - коэффициент теплопроводности, - градиент температуры.

Единичный вектор в направлении нормали и изотермической поверхности. Градиент температуры направлен по нормали к изотермической поверхности в сторону возрастания температуры.

Рассмотрим несколько подробнее понятие изотермической поверхности и градиента температуры.

Если в каждый конкретный момент времени нам известны температуры в любой точке тела, то, очевидно, нам известно температурное поле, которое, в общем, будет функцией четырех переменных (трех координат декартовой или любой другой системы и времени).

В любой системе с произвольным температурным полем можно найти точки равной температуры, если соединить их некоторой поверхностью, то получится изотермическая поверхность, поверхность равного уровня.

Таким образом, изотермическую поверхность можно определить как изотермическое место точек с равной температурой. Коль скоро любая точка тела может иметь лишь одну температуру в данный момент времени, то изотермические поверхности никогда не пересекаются с собой.

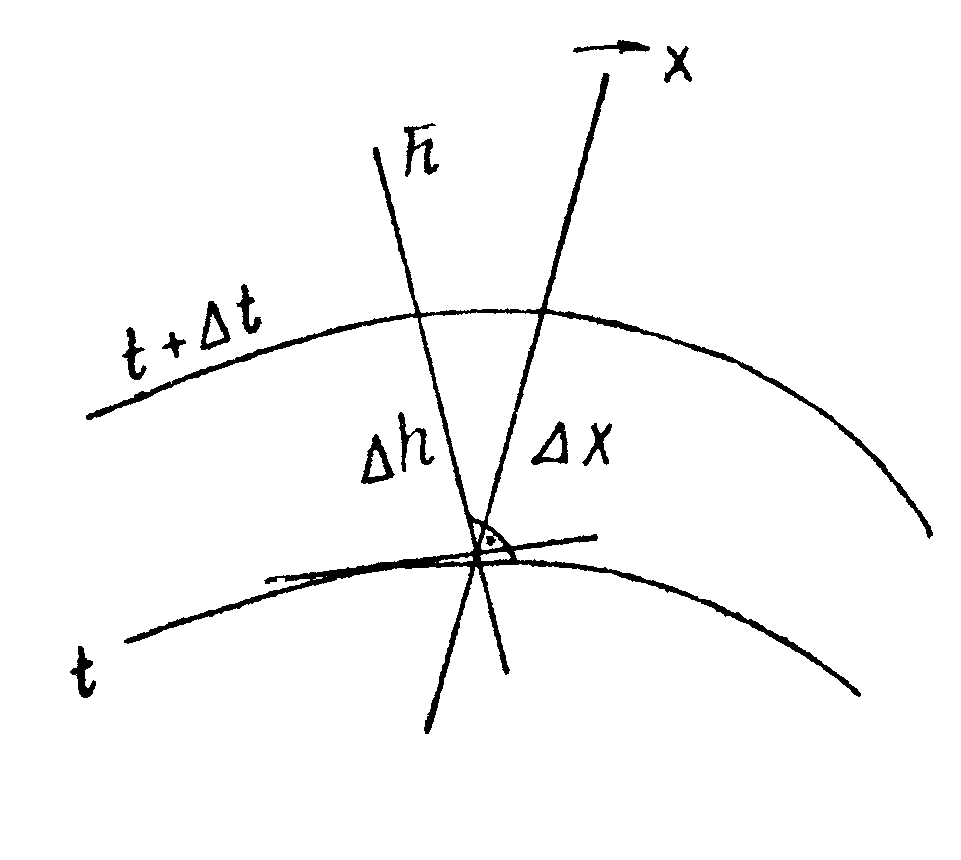
Рисунок 1.1 – Температурный градиент.

Температура тела меняется от изотермы к изотерме. Скорость изменения температуры на единицу длины наибольшая в направлении нормали к изотермической поверхности. Тогда предел отношения изменения температуры к расстоянию по нормали к изотермическим поверхностям называется градиентом температуры.

Фурье на основе обобщения опытных фактов установил записанную выше зависимость.

Тепло, как следует из второго начала термодинамики, самопроизвольно может переходит лишь от более нагретого к менее нагретому. Это приводит к появлению знака минус в уравнении Фурье.

То есть тепловой поток имеет всегда направление противоположное градиенту температуры

Коэффициент пропорциональности называется коэффициентом теплопроводности. Он характеризует физические свойства вещества, его способность проводить тепло

Он представляет собой количество тепла, которое проходит в единицу времени через единицу изотермической поверхности при единичном температурном градиенте

Коэффициент теплопроводности зависит от структуры, плотности, влажности, температуры, давления.

Для теплоизоляционных строительных материалов

Для газов

Для решаемого в лабораторной работе случая стационарного одномерного поля градиент температуры равен

На основании закона Фурье запишем

(1.13)

Преобразуем выражение (13), подставив величину шаровой изотермической поверхности

,

тогда

,

откуда определим коэффициент теплопроводности

, (1.14)

где - разность температур между внутренней и внешней поверхностью шара. Последняя формула (1.14) является исходной для расчета коэффициента теплопроводности материала шарового кольца.