4.2 Валидация модели
Проведем валидацию модели методом сопоставления результатов моделирования с результатами аналитических расчетов.
Интенсивность поступления заявок (плотность потока):
Интенсивность обслуживания:
Коэффициент использования обслуживающего устройства:
Поскольку
коэффициент 
больше 1, формулы для аналитического
подсчета характеристик применить
невозможно. В связи с этим, ограничимся
сравнением одной характеристики –
времени, необходимого для полной
обработки одной задачи.
Характеристика |
Модельное время |
Расчетное время |
Отклонение |
Обработка одной задачи |
25 |
22,5 |
10% |
Отклонение в 10% позволяет судить о правильности построения модели.
5. Планирование и проведение имитационных экспериментов
5.1 Определение средней очереди к памяти, средней загрузки памяти, процессора и базы данных.
Средний размер очереди к ОЗУ составляет 0.000, что говорит об отсутствии необходимости в накопителе перед ОЗУ, либо о возможности значительно увеличивать значения объема ОЗУ, требуемые для загрузки задачи, т.е. решать более ресурсоемкие задачи.
Для определения загрузки ОЗУ необходимо определить число прогонов модели для получения с точностью 0,1 и доверительной вероятностью 0,95.
,
где
- квантиль нормального распределения вероятностей, определяемый из таблицы распределения Стьюдента.
- дисперсия
случайной величины.
- заданная точность.
Дисперсию случайной величины определяем по формуле
,
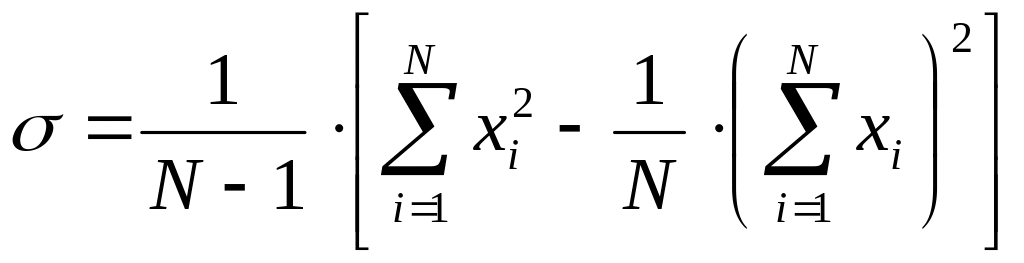где
N – 50-100 пробных прогонов системы.
Для определения коэффициента Стьюдента найдем число степеней свободы:
k = n-1-m = 3-1-1=1, где
n – число значений (интервалов) случайной величины,
m – количество определяемых параметров.
= 3.182
= 0,1
Также необходимо определить дисперсию случайной величины для позиции Р3. Для этого проведём 100 пробных прогонов модели.
= 0,23
Тогда N = 54
После 54 прогонов получаем среднее значение загрузки ОЗУ, равное 0,4967.
Для определения загрузки процессора найдем дисперсию случайной величины.
= 0,19
Тогда N = 37
После 37 прогонов получаем среднее значение загрузки ЦП, равное 0,92.
Для определения загрузки базы данных найдем дисперсию случайной величины.
= 0,35
Тогда N = 125
После 37 прогонов получаем среднее значение загрузки БД, равное 0,8598.
5.2. Результаты моделирования.
В
концептуальной модели были смоделированы
двое суток (2880 временных единиц – минут)
работы вместо указанных в задание пяти
в связи с ограничением максимального
количества блоков в студенческой версии
программы.
Задачи подавались каждые 20 мин.
Результаты за один прогон модели: за двое суток моделирования поступило на обработку 143 задачи, 142 из которых были обработаны.
Перед занятием задачей ОЗУ, поступлением задачи на обработку ЦП и выводом результатов в БД было установлено 3 накопителя – RAMOCH, CPOCH и BDOCH соответственно. Максимальное количество задач в первом и втором накопителях составило 1, в третьем – 7. Средний размер очереди – 0, 0.125 и 1.586 соответственно.
Исходя из полученных данных, можно утверждать, что процессор и база данных используются эффективно, а ОЗУ работает лишь на 50% своих возможностей. Модель без потери производительности может обрабатывать задачи, требующие в 2 раза больше оперативной памяти для обработки.