Симплексный метод (назначение метода, симплексные таблицы, правило построения симплекс-таблиц, понятия индексной строки, разрешающего элемента, правило прямоугольника).
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Симплексный метод (назначение метода, признаки бесконечного множества решений, неограниченности целевой функции, несовместности системы).
Симплексный метод (назначение метода, признаки бесконечного множества решений, неограниченности целевой функции, несовместности системы).
Назначение метода
В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Идея симплекс-метода заключается в следующем. Сначала нужно найти некоторую (начальную) вершину многогранника допустимых решений (начальное допустимое базисное решение). Затем нужно проверить это решение на оптимальность. Если оно оптимально, то решение найдено; если нет, то перейти к другой вершине многогранника и вновь проверить на оптимальность. Ввиду конечности вершин многогранника (следствие конечности ограничений задачи ЛП) за конечное число "шагов" мы найдем искомую точку минимума или максимума. Надо заметить, что при переходе от одной вершины к другой значение целевой функции убывает (в задаче на минимум) или возрастает (в задаче на максимум).
Неограниченность целевой функции
Если в ведущем столбце нет ни одного строго положительного элемента, то задача не имеет оптимального решения, а целевая функция неограниченна снизу (в задаче на минимум) или неограниченна сверху (в задаче на максимум).
Бесконечное множество решений
Если в последней (оптимальной) таблице оценка какой-либо небазисной переменной (число в нулевой строке) равна нулю, то задача имеет бесконечное множество оптимальных решений.
Несовместимость системы
Обнаруживается при построении начального допустимого базисного решения (оно не существует).
Двойственные задачи в линейном программировании (понятие двойственности, построение пары взаимно двойственных задач, правила построения, примеры).
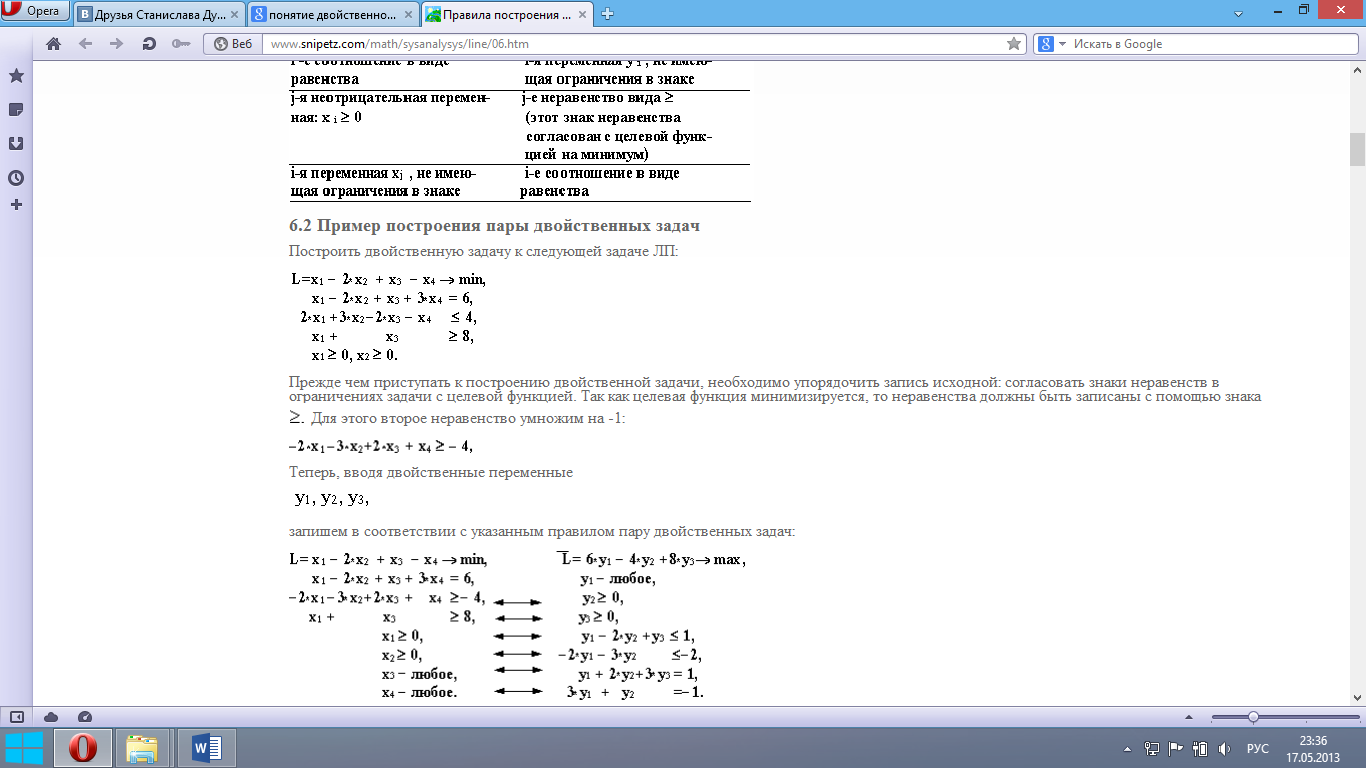
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как целевая функция минимизируется, то неравенства должны быть записаны с помощью знака Для этого второе неравенство умножим на -1:
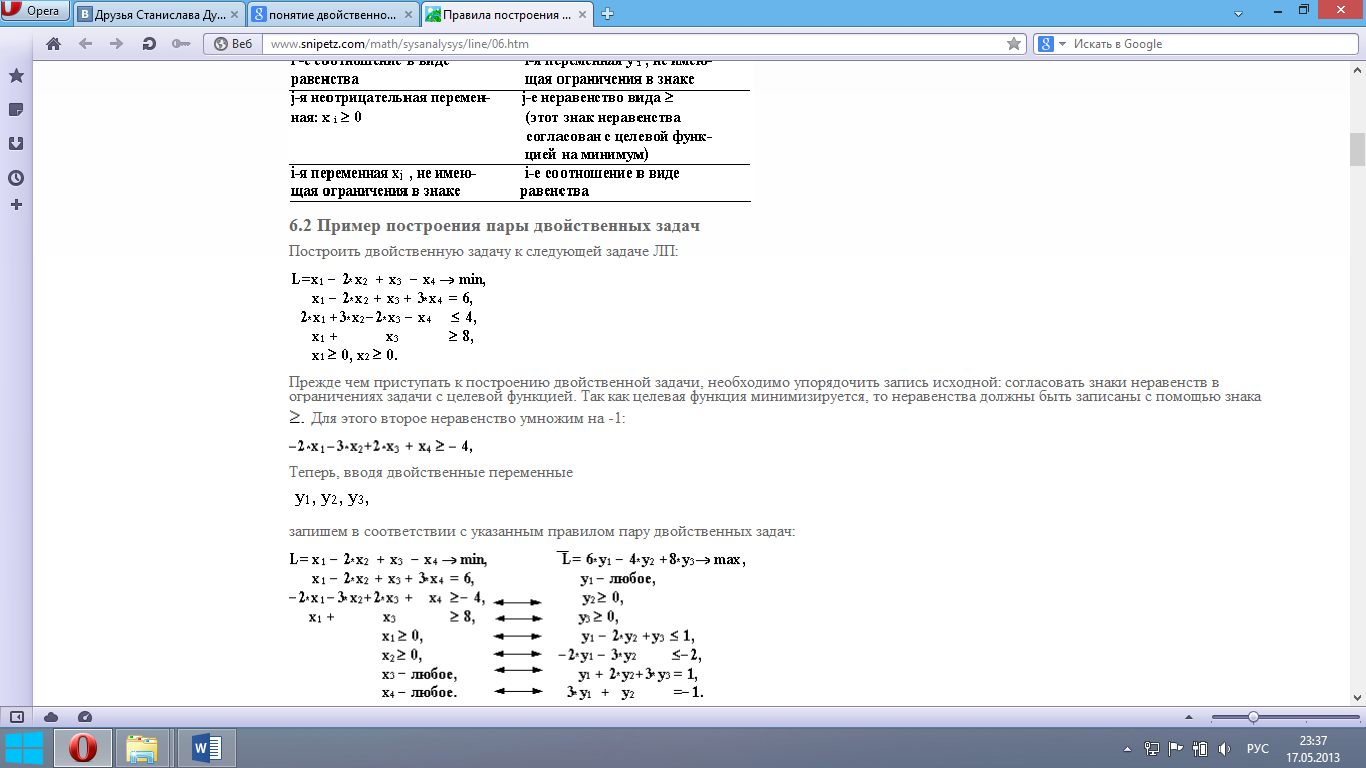
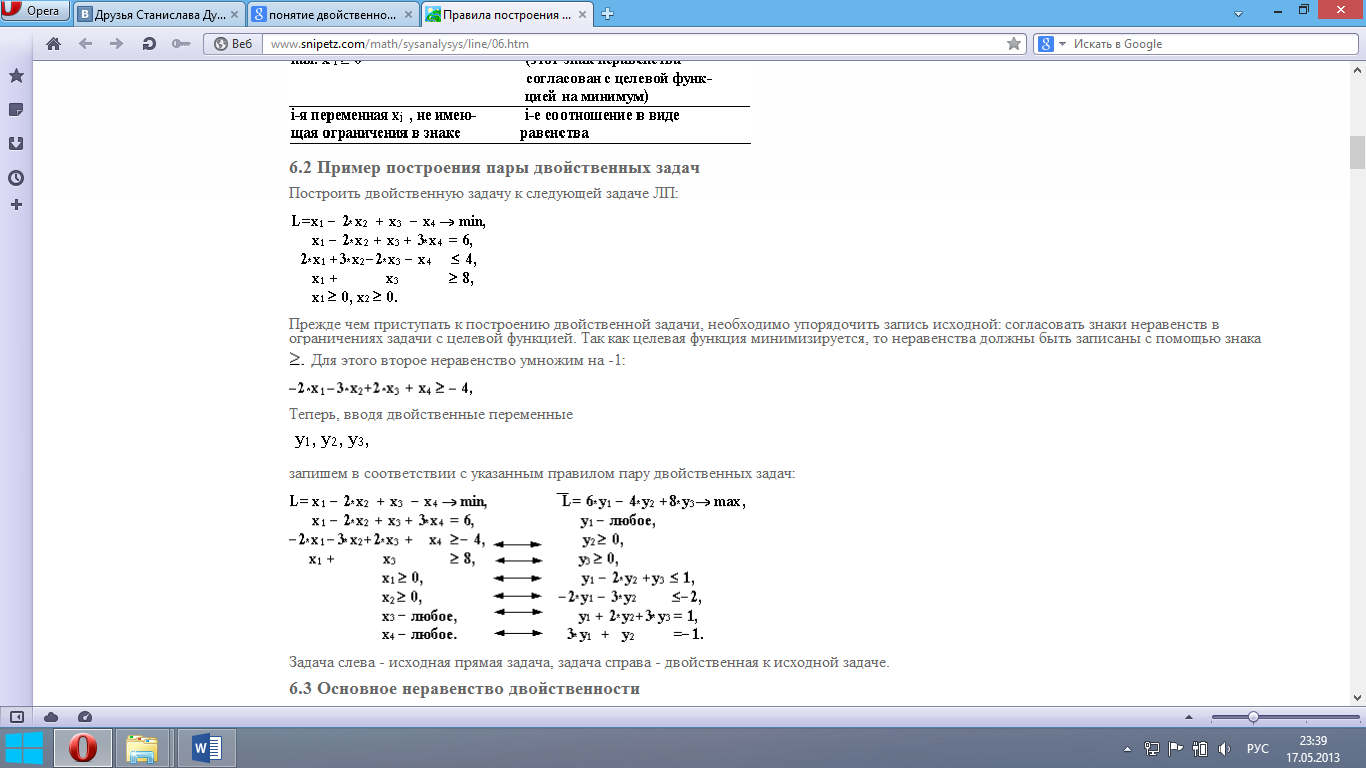
Двойственные задачи в линейном программировании (формулировка второй теоремы двойственности, соответствие между переменными, экономическая интерпретация дополнительных переменных в двойственной задаче).
Задачу (1) называют прямой, а связанную с ней задачу (2) – двойственной. Вместе они образуют симметрическую пару двойственных задач. Число переменных двойственной задачи равно количеству ограничений прямой. Кроме того, при переходе от прямой задачи к двойственной вектора B и C меняют местами, матрица A коэффициентов системы ограничений прямой задачи транспонируется, а знак неравенств в ограничениях меняют на противоположный. Смысл экстремума F(x) противоположен смыслу экстремума F(y) . Связь между задачами (1) и (2) взаимна, т.е. если прямой считать задачу (2), то в качестве двойственной ей будет соответствовать задача (1). Возможность перехода от прямой задачи к двойственной (и наоборот) устанавливается теоремой двойственности: если одна из задач (1) или (2) имеет оптимальное решение, то и другая также имеет оптимальное решение, причем оптимальные значения функции цели прямой и двойственной задач совпадают, т.е. max F(x) = min F( y). Если среди ограничений прямой задачи имеются равенства или на некоторые переменные не наложено условие неотрицательности, то построив двойственную ей задачу, получим пару несимметричных двойственных задач: