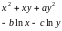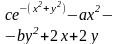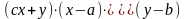Контрольные вопросы
Постановка задачи поиска экстремума функции одного переменного.
Дайте понятие локального и глобального экстремума функции одного переменного.
Выпуклые и вогнутые функции.
Алгоритмы поиска экстремума функции одного переменного методами золотого сечения и половинного деления.
Определение количества шагов итераций методами золотого сечения и половинного деления.
Критерий окончания поиска экстремума методами золотого сечения и половинного деления.
Лабораторная работа № 10 Поиск экстремума функции многих переменных без ограничений градиентными методами
Задание: найти точку глобального экстремума функции двух переменных заданным методом с погрешностью = 0,05.
Варианты заданий
№ вар |
Целевая функция |
a |
b |
c |
Тип экстремума |
x0 |
y0 |
Метод |
|
|
|
2 |
1 |
3 |
min |
.3 |
.5 |
наискор спуска |
|
|
- “ - |
3 |
2 |
4 |
min |
.3 |
.5 |
релакс. |
|
|
- “ - |
3 |
1 |
2 |
min |
.5 |
.3 |
Ньютона-Рафсона |
|
|
- “ - |
2 |
1 |
3 |
min |
.5 |
.3 |
релакс. |
|
|
- “ - |
3 |
2 |
4 |
min |
.2 |
.5 |
Ньютона-Рафсона |
|
|
|
3 |
1 |
2 |
min |
.5 |
.02 |
наискор спуска |
|
|
|
1.5 |
2 |
1 |
min |
.5 |
.3 |
наискор спуска |
|
|
- “ - |
.5 |
3 |
2 |
min |
.3 |
.5 |
релакс. |
|
|
- “ - |
2.5 |
2 |
1 |
min |
.1 |
.3 |
Ньютона-Рафсона |
|
|
- “ - |
1.5 |
2 |
1 |
min |
.3 |
.1 |
релакс. |
|
|
- “ - |
.5 |
3 |
2 |
min |
.5 |
.3 |
Ньютона-Рафсона |
|
|
- “ - |
2.5 |
2 |
1 |
min |
.3 |
.5 |
наискор спуска |
|
|
|
1 |
1 |
1 |
max |
.5 |
.2 |
крутого восхожд. |
|
|
- “ - |
1 |
1 |
2 |
max |
.2 |
.5 |
релакс. |
|
|
- “ - |
1.5 |
1 |
2 |
max |
.5 |
.2 |
Ньютона-Рафсона |
|
|
- “ - |
1 |
1 |
1 |
max |
.4 |
.2 |
релакс. |
|
|
- “ - |
1 |
1 |
2 |
max |
.2 |
.9 |
Ньютона-Рафсона |
|
|
- “ - |
1.5 |
1 |
2 |
max |
.8 |
.2 |
наискор спуска |
|
|
|
0,5 |
-1 |
2 |
min |
.2 |
.5 |
наискор спуска |
|
|
|
1 |
-1 |
2 |
min |
.5 |
.2 |
релакс. |
|
|
- “ - |
1 |
-1 |
3 |
min |
.2 |
.5 |
Ньютона-Рафсона |
|
|
- “ - |
0,5 |
-1 |
2 |
min |
.6 |
.2 |
релакс. |
|
|
- “ - |
1 |
-1 |
2 |
min |
.2 |
.2 |
Ньютона-Рафсона |
|
|
- “ - |
1 |
-1 |
3 |
min |
.2 |
.6 |
наискор спуска |
|
|
|
2 |
3 |
1 |
max |
.1 |
0 |
крутого восхожд. |
|
|
- “ - |
2 |
3 |
2 |
max |
.5 |
0 |
релакс. |
|
|
- “ - |
1 |
3 |
2 |
max |
0.3 |
0 |
Ньютона-Рафсона |
|
|
- “ - |
2 |
3 |
1 |
max |
0 |
.4 |
релакс. |
|
|
- “ - |
2 |
3 |
2 |
max |
0 |
.5 |
Ньютона-Рафсона |
|
|
- “ - |
1 |
3 |
2 |
max |
0 |
0.3 |
крутого восхожд. |
