- •(Фгбоу впо "ВятГу")
- •Часть 2
- •Лабораторная работа № 8 решение задач стохастического программирования
- •Содержание отчёта
- •Лабораторная работа № 9 сетевое планирование управления (спу)
- •Содержание отчёта
- •Лабораторная работа № 9 Поиск экстремума функции одной переменной методами золотого сечения и половинного деления
- •Варианты заданий
- •Ход работы
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 10 Поиск экстремума функции многих переменных без ограничений градиентными методами
- •Варианты заданий
- •Ход работы
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 11 Оптимизация при сепарабельных целевой функции и ограничениях
- •Варианты заданий
- •Содержание отчета
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 13 Задача управления запасами
- •Варианты заданий
- •Содержание отчета
- •Контрольные вопросы
- •Лабораторная работа № 14 Имитационное моделирование системы массового обслуживания (смо)
- •РекомендуемАя литература
- •Содержание
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования «Вятский государственный университет»
(Фгбоу впо "ВятГу")
ФАКУЛЬТЕТ ЭКОНОМИКИ И МЕНЕДЖМЕНТА
МАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным работам для студентов
специальности Математические методы в экономике
и направлений Прикладная информатика и Бизнес-информатика
Часть 2
Киров 2011
УДК. 681.3.06:519.682
Математические методы и модели исследования операций. Методические указания к лабораторным работам для студентов специальности Математические методы в экономике и направлений Прикладная информатика и Бизне-информатика. Часть 2. - Киров, 2011. - с.38.
Составитель: к.т.н., доцент Л.А. Нестерова
Рецензент:
Ⓒ Вятский государственный университет
Лабораторная работа № 8 решение задач стохастического программирования
Задача стохастического программирования в М-постановке – это максимизация (минимизация) математического ожидания (среднего значения) целевой функции.
Математическая постановка задачи записывается:

где αi – задаваемый уровень вероятности, с которой должно выполняться i-тое ограничение;
Детерминированный эквивалент задачи в М-постановке имеет вид
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
Достаточно
часто
 - дисперсия случайной величины aij
и
- дисперсия случайной величины aij
и
 - дисперсия случайной величины bi
бывают неизвестны. В этом случае можно
задать для случайных величин значения
коэффициентов вариабельности v[x]
и для определения дисперсий воспользоваться
формулой
- дисперсия случайной величины bi
бывают неизвестны. В этом случае можно
задать для случайных величин значения
коэффициентов вариабельности v[x]
и для определения дисперсий воспользоваться
формулой

Пример
В качестве примера рассмотрим задачу распределения ресурсов.
Предприятие выпускает продукцию четырех типов П1, П2, П3 и П4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье и финансы. Для выпуска единицы продукции П1 требуется 1 ед. трудовых ресурсов, 6 ед. сырья и 4 ед. финансов, ожидаемая прибыль от реализации единицы продукции П1 составляет 60 у.е. Аналогичные показатели для продукции П2 имеют значения – 1, 5, 6 и 70; для П3 – 1, 4, 10 и 120, для П4 – 1, 3, 13 и 130. Количество ресурсов каждого вида ограничено и составляет: Определить объемы выпускаемой продукции, при которых получаемая предприятием прибыль будет максимальной. Потребность каждого вида ресурса на производство единицы продукции каждого типа, а также имеющиеся в наличии объемы ресурсов приведены в таблице:
Составление математической модели
|
Математическая модель: ЦФ F = 60x1 + 70x2 +120x3 + 130 x4 (1) x1 + x2 + x3 + x4 ≤ 16 ОГР 6x1 + 5x2 + 4x3 + 3x4 ≤ 110 (2) 4x1 + 65x2 + 10x3 + 13x4 ≤ 100 x1≥0, x2 ≥0, x3 ≥ 0, x4 ≥ 0 |
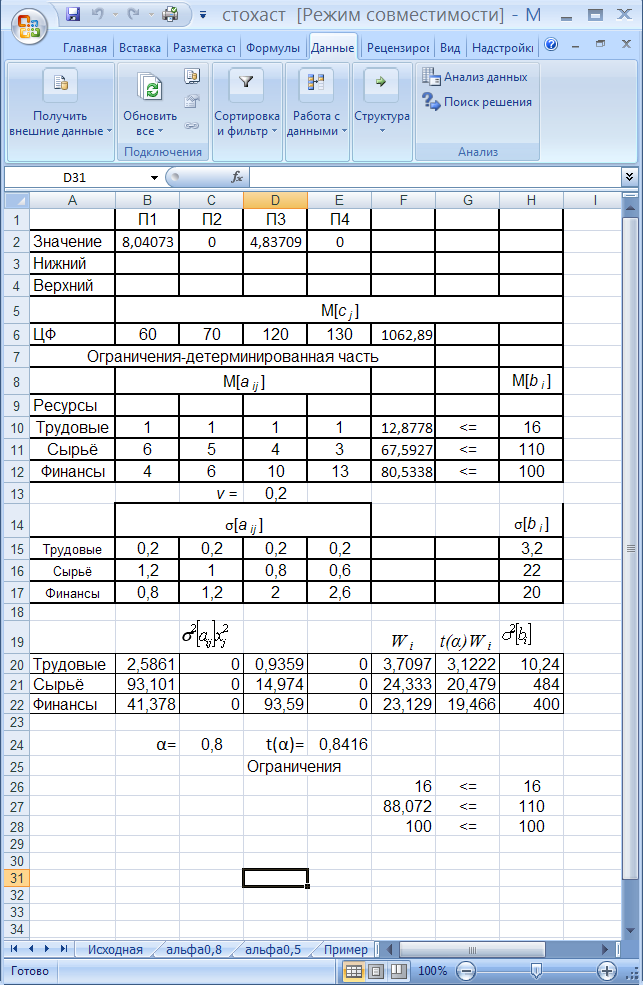
В качестве математических ожиданий параметров модели примем заданные в условиях задачи значения. Введём значения объёмов выпускаемой продукции, равные 1 (рис. 1). Примем уровень вероятности, с которой должно выполняться i-тое ограничение равным 0,8.
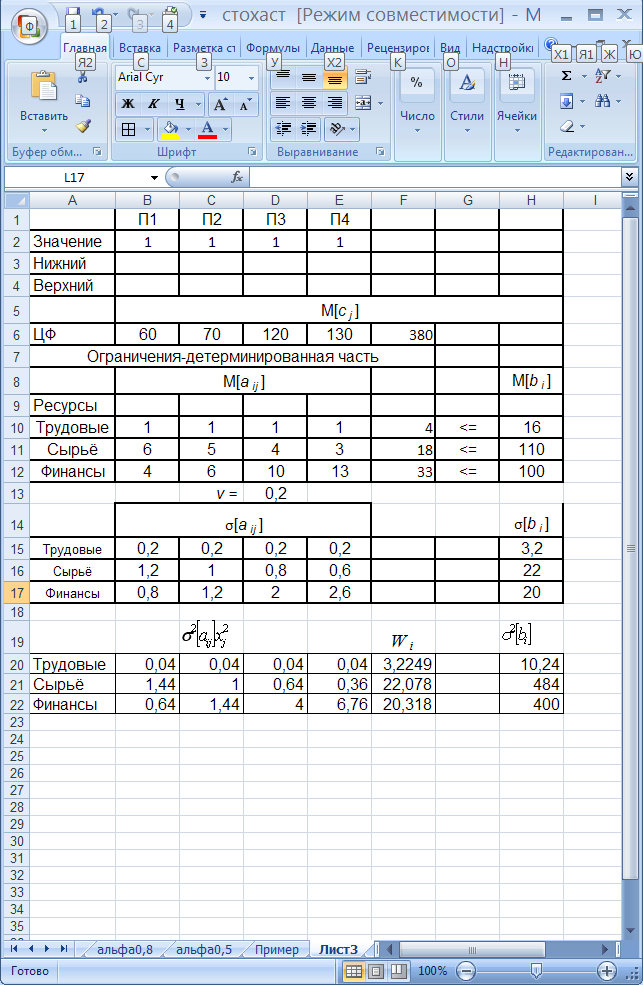
Рисунок 1 Условия задачи
Зададим коэффициент вариабельности для всех коэффициентов и правых частей ограничений одинаковым и равным 0,2.
Вычислим и для всех параметров ограничений по формуле

Рисунок 2 Расчёт дисперсии параметров ограничений
Для
вычисления Wi,
вычислим сначала подсчитаем
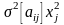 ,
введя в ячейку В20 формулу (B$2*B15)^2
и скопировав её в остальные ячейки
правых частей ограничений, а затем -
,
введя в ячейку В20 формулу (B$2*B15)^2
и скопировав её в остальные ячейки
правых частей ограничений, а затем -
 .
В каждой строке найдём
Wi по формуле
.
.
В каждой строке найдём
Wi по формуле
.
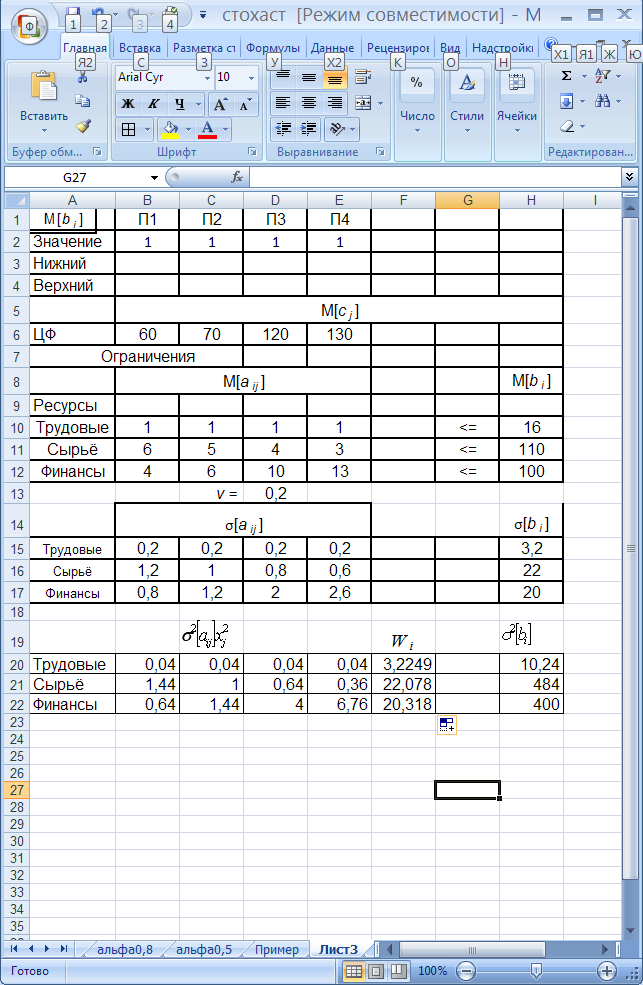
Рисунок 3 Вычисление Wi
t(αi)Wi – величина дополнительного ресурса, который требуется вследствие вероятности исходных данных.
Для заданного уровня вероятности, с которой должно выполняться i-тое ограничение найдём значение случайной величины t, имеющей стандартное нормальное распределение. Для этого воспользуемся статистической функцией НОРМСТОБР:
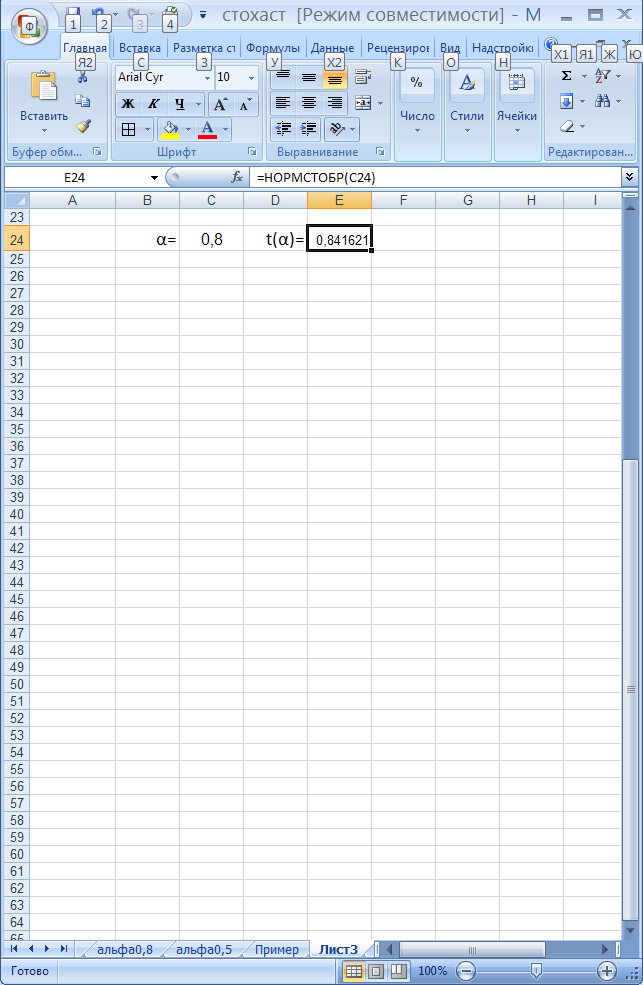
Для каждого ограничения вычисляем t(α)Wi и формируем ограничения (2):
Рисунок 1 Формирование ограничений
Для поиска максимума целевой функции вызываем диалоговое окно Поиск решения, в котором устанавливаем целевую ячейку, изменяемые ячейки и вводим ограничения задачи. При этом имеем в виду, что модель нелинейная, так как содержит в ограничениях xi2.
 Рисунок
5
Рисунок
5
Решение задачи в детерминированном виде:
 Рисунок 6
Рисунок 6
Из сравнения решений обеих задач видим, что значение целевой функции ухудшилось на:
β = 100% * |F0 – F|/F0= (1320 - 1062,89)/1320*100% = 19,48%.
По каждому виду ресурсов создан запас
Δi
= 100% * t(α)Wi
/| + t(α)Wi
|
+ t(α)Wi
|
по трудовым ресурсам 19,51%, по сырью 18,62%, по финансам 19,47%.
Рассмотренная задача может быть решена и как целочисленная. Для этого в поле Ограничения диалогового окна Поиск решения нужно ввести условие целочисленности для всех переменных.
 Рисунок 7
Рисунок 7
Значение целевой функции стало ещё меньше.
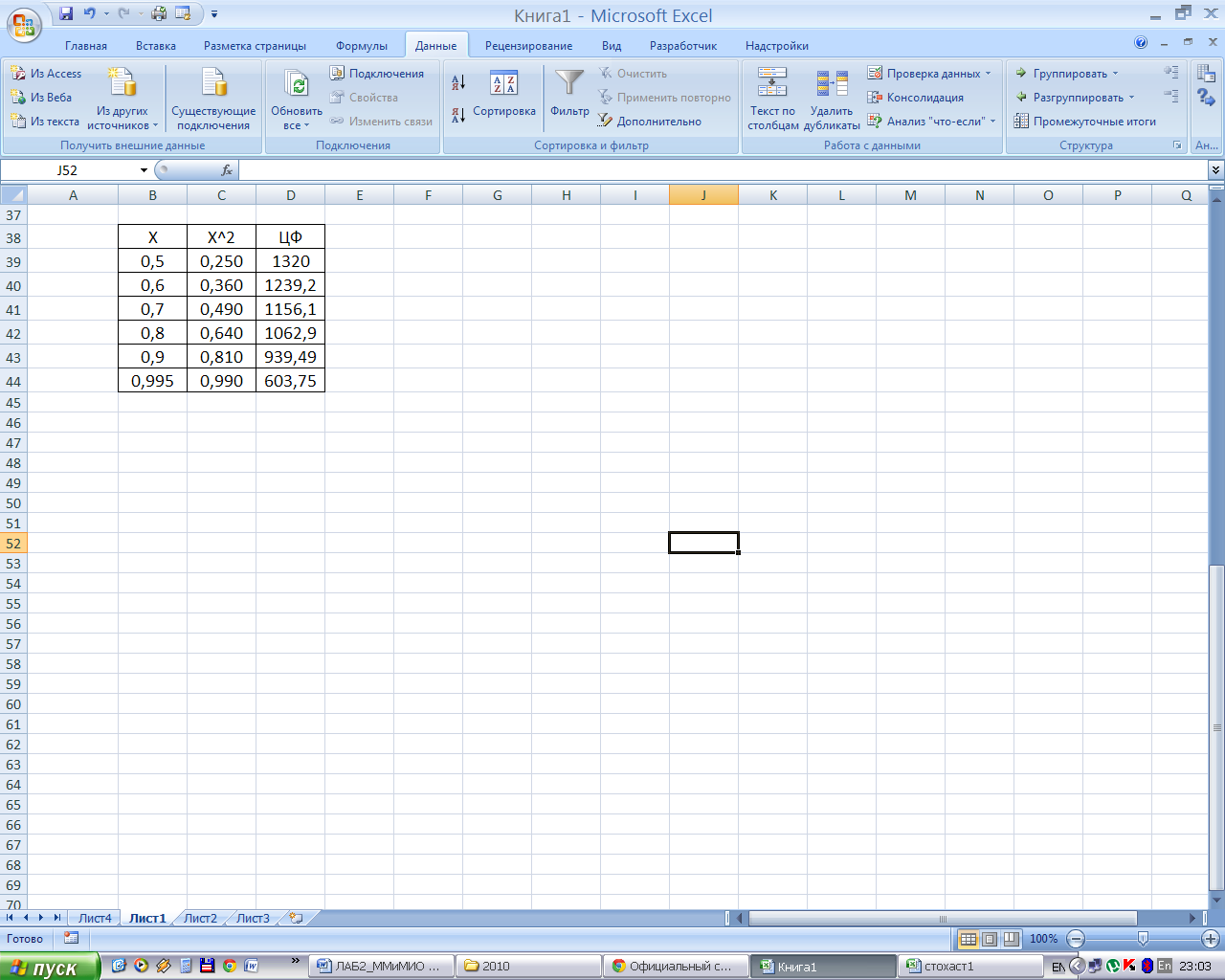
Исследуем влияние уровня вероятности, с которой должно выполняться i-тое ограничение, на результат решения. С этой целью зададимся следующими значениями αi : 0,5; 0,6; 0,7; 0,8; 0,9; 0,95 и 0,995. Результаты моделирования приведены в таблице:
α |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,995 |
П1 |
10 |
9,383 |
8,750 |
8,041 |
7,104 |
6,363 |
4,562 |
П2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
П3 |
6 |
5,635 |
5,259 |
4,837 |
4,277 |
3,833 |
2,750 |
П4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
ЦФ |
1320 |
1239,2 |
1156,1 |
1062,9 |
939,49 |
841,81 |
603,75 |
Трудовые |
16 |
15,018 |
14,009 |
12,878 |
11,381 |
10,197 |
7,3125 |
Сырьё |
84 |
78,837 |
73,538 |
67,593 |
59,732 |
53,514 |
38,375 |
α |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,995 |
Финансы |
100 |
93,881 |
87,594 |
80,534 |
71,187 |
63,787 |
45,75 |
Запасы |
|
|
|
|
|
|
|
Трудовые |
0 |
6,14% |
12,44% |
19,51% |
28,87% |
36,27% |
54,30% |
Сырьё |
0 |
5,79% |
11,79% |
18,62% |
27,78% |
35,12% |
53,34% |
Финансы |
0 |
6,12% |
12,41% |
19,47% |
28,81% |
36,21% |
54,25% |
По результатам решения можно построить графики, показывающие влияние вероятности выполнения ограничений задачи на значение целевой функции (рис.8), объём выпускаемой продукции (рис.9) и размер создаваемых запасов ресурсов (рис.10).
|
|
Рисунок 8 Рисунок 9
 Рисунок
10
Рисунок
10
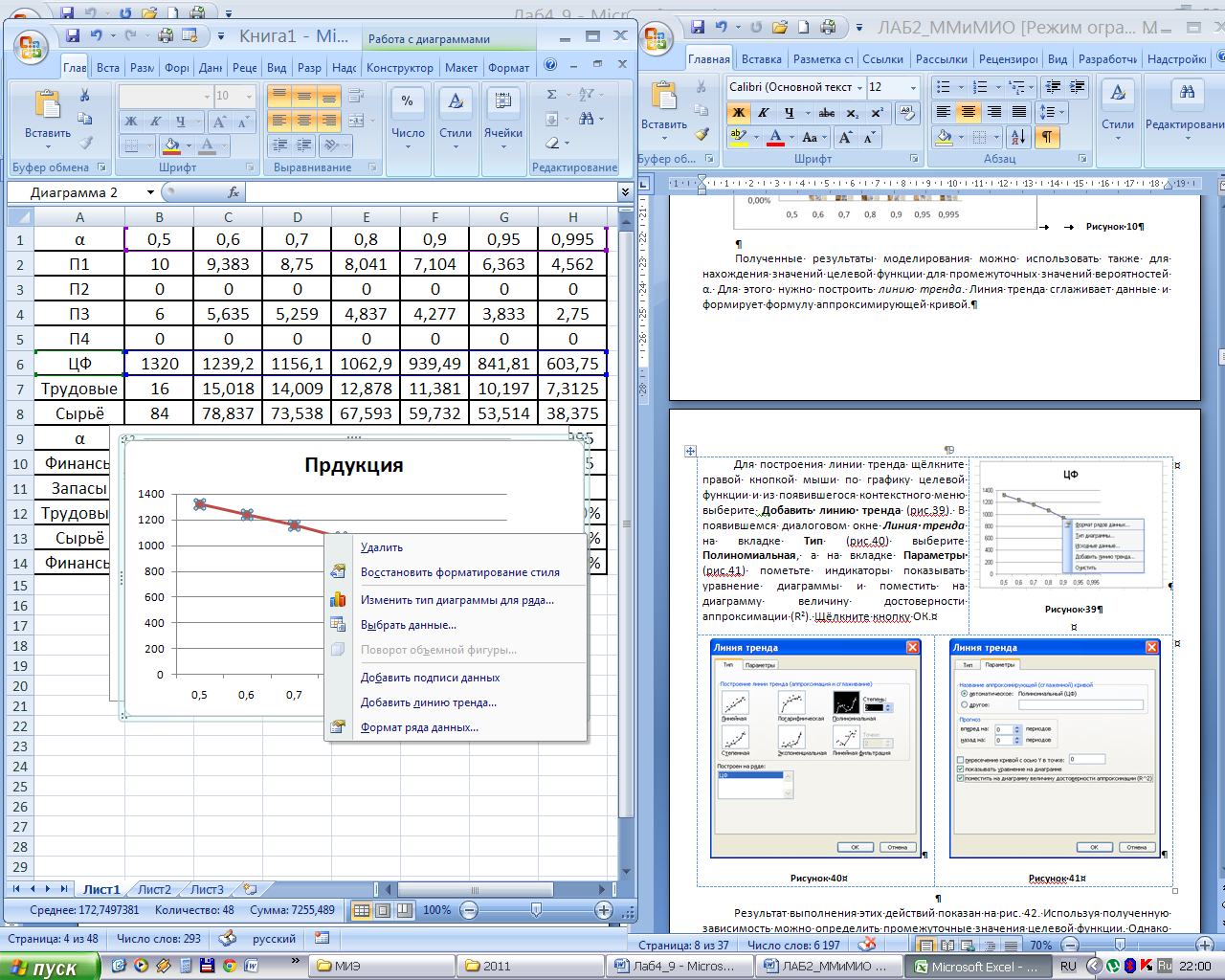
Полученные результаты моделирования можно использовать также для нахождения значений целевой функции для промежуточных значений вероятностей α. Для этого нужно построить линию тренда. Линия тренда сглаживает данные и формирует формулу аппроксимирующей кривой.
Для построения линии тренда щёлкните правой кнопкой мыши по графику целевой функции и из появившегося контекстного меню выберите Добавить линию тренда (рис.11).
|
Рисунок 11 |
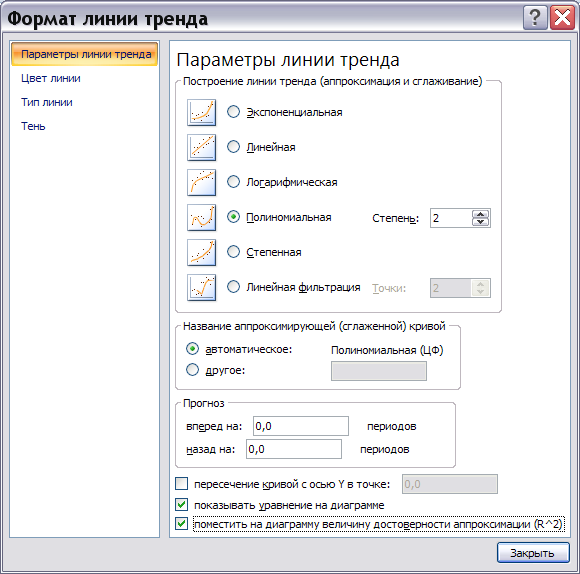
В появившемся диалоговом окне Формат линии тренда на вкладке Параметры линии тренда (рис.12) выберите Полиномиальная и пометьте индикаторы Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R^2). Щёлкните кнопку Закрыть.
|
Рисунок 12 |
Результат выполнения этих действий показан на рис. 13. Используя полученную зависимость можно определить промежуточные значения целевой функции. Однако следует иметь в виду, что для построения линии тренда Excel использует в качестве х номер периода, а не значения оси абсцисс (рис. 14).
Рисунок 13 |
Рисунок 14 |
В связи с изложенным, нужно иметь ввиду, что для построения достоверной линии тренда в Excel нужно брать шаг независимой переменной одинаковым. В нашем случае можно использовать шаг по α, равным 0,1 (рис.15). Как видно из рис.15, уравнение линии тренда изменилось. |
|
Для получения коэффициентов аппроксимирующей полиномиальной зависимости вида
урасч = а0 + а1* α + а2*α2
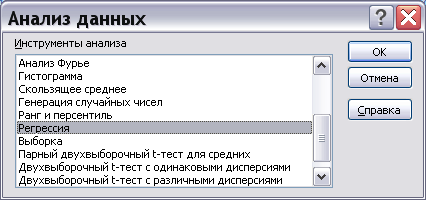
можно использовать Средства анализа данных, предлагаемые на вкладке Анализ ленты инструментов Данные.
Проверка значимости уравнения регрессии проводится по F-критерию (критерию Фишера). В Excel используются следующие формулы:

где n – количество пар значений х-у, (для нашего примера n = 6).
Рисунок 16 |
Рисунок 17 |
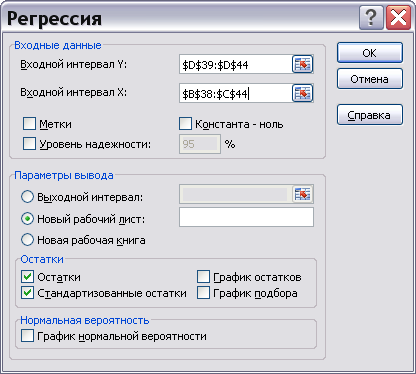
Исходные данные для расчёта можно представить в виде таблицы (рис.16). При нажатии кнопки Средства анализа данных появляется диалоговое окно Анализ данных. В качестве инструмента анализа выбираем Регрессия.
В диалоговом окне Регрессия (рис.17) введите интервалы значений у, пометьте индикаторы Остатки и Стандартизированные остатки и нажмите кнопку ОК.
 Рисунок
18
Рисунок
18
На новом рабочем листе будут выведены результаты анализа (рис.19).
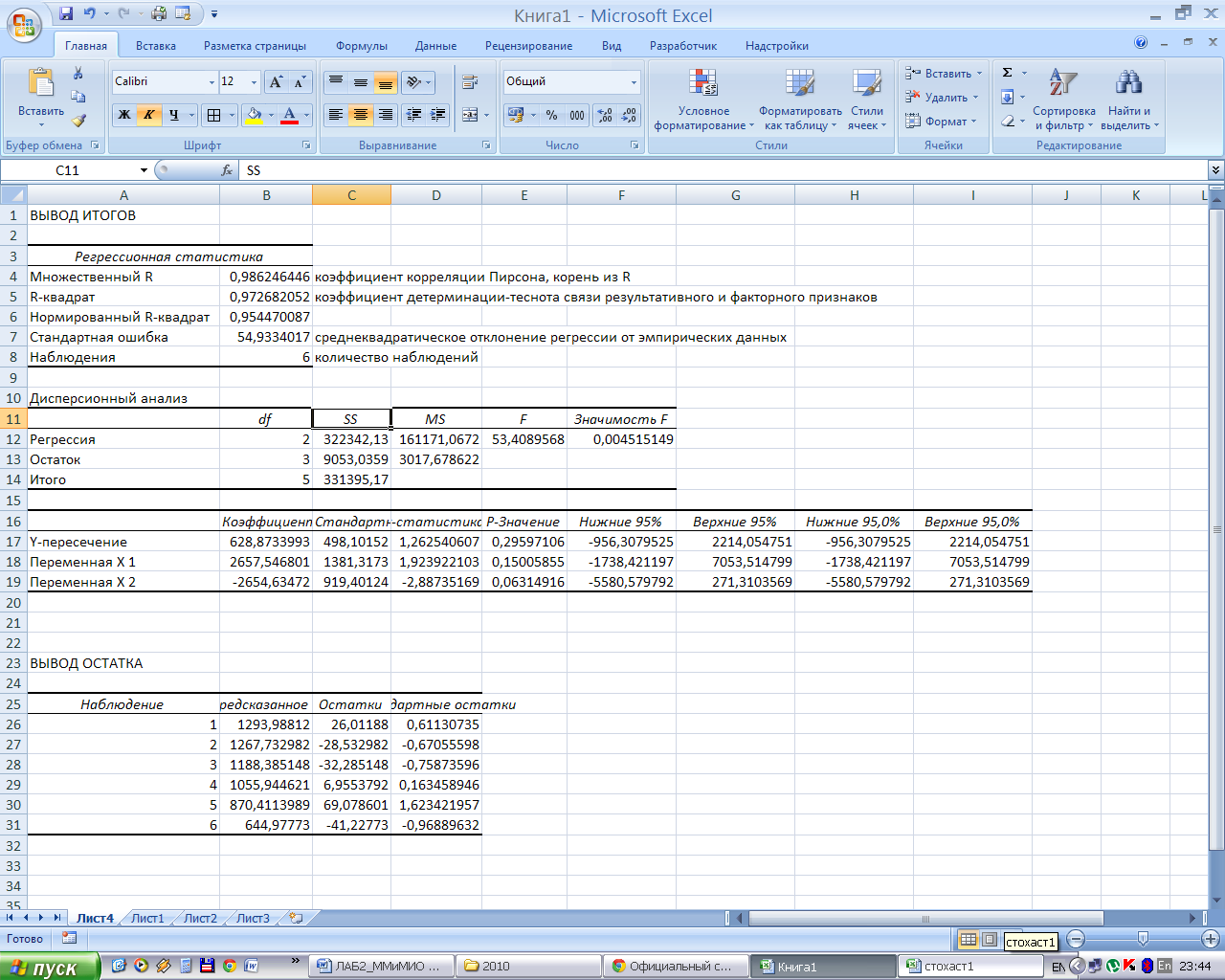
Рисунок 19
Найденная полиномиальная зависимость будет иметь вид:
урасч = 628,9 + 2657,6* α – 2654,6*α2
Табличное значение критерия Фишера для уровня значимости 0,05 для числа степеней свободы k1 = 5 , k2 = 3 F1-0,5,5,3 = 6,16. Расчётное значение критерия больше табличного при заданном уровне значимости, то есть модель адекватна исходным данным с вероятность 0,95.
Задание.
В соответствии с заданным вариантом получите решение задачи для уровня вероятности, с которой должно выполняться i-тое ограничение равным 0,6. Выведите все виды отчётов для найденного решения.
Получите решение задачи в детерминированном виде: (α = 0,5).
Получите решение задачи для следующих значений αi : 0,5; 0,6; 0,7; 0,8; 0,9; 0,95 и 0,995. Сведите решение задачи в таблицу.
По результатам решения постройте графики и гистограммы, показывающие влияние вероятности выполнения ограничений задачи на значение целевой функции, объём выпускаемой продукции и размер создаваемых запасов ресурсов.
Постройте линию тренда для целевой функции, выбрав зависимость, которая имеет наибольший показатель достоверности.
Постройте линию тренда для целевой функции, используя шаг по α, равным 0,1.
Получите аппроксимирующую функцию средствами анализа данных.
Получите решения задачи для уровня вероятности, с которой должно выполняться лимитирующее ограничение, установленное в детерминированном решении (п.2).
По результатам решения постройте графики и гистограммы, показывающие влияние вероятности выполнения ограничений задачи на значение целевой функции, объём выпускаемой продукции и размер создаваемых запасов ресурсов.



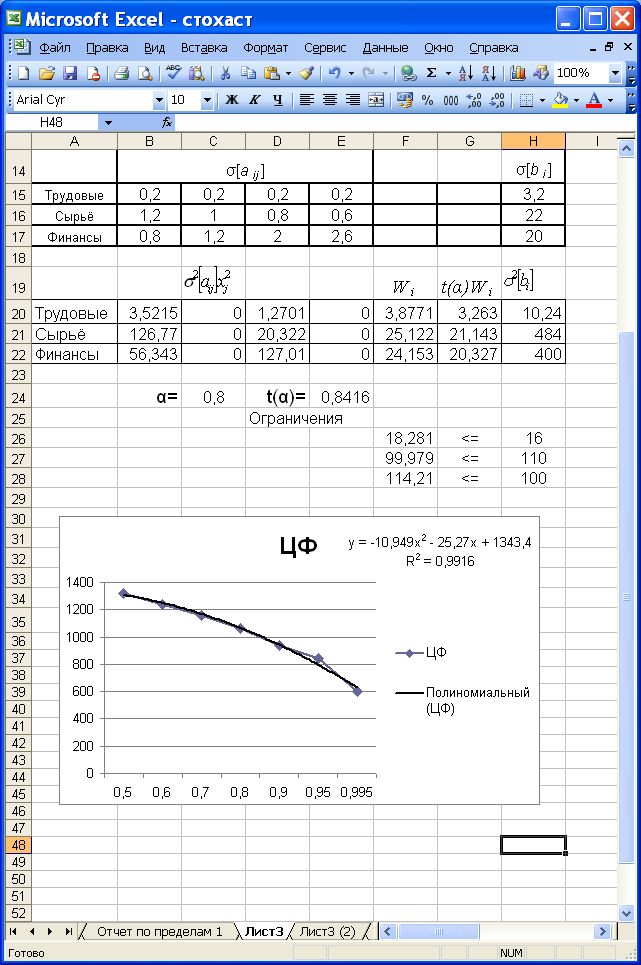
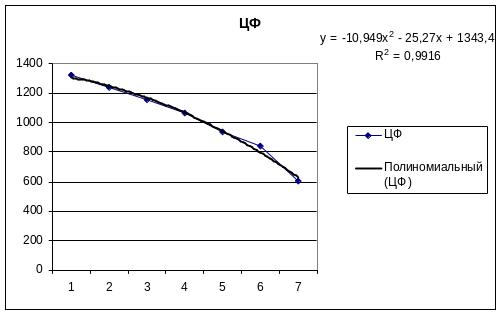
 Рисунок
15
Рисунок
15