31

Лекция 2. Принципы создания инверсной населенности.

Инверсная населенность и усиление света. Балансные уравнения для населенности в стационарных и нестационарных условиях: 3 и 4 уровневые схемы. Принципы создания инверсной населённости. Электрическая накачка в газах. Химическая накачка. Термодинамическая накачка. Другие виды накачки. Оптическая накачка, резонансное возбуждение.

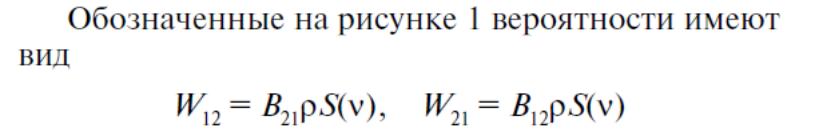
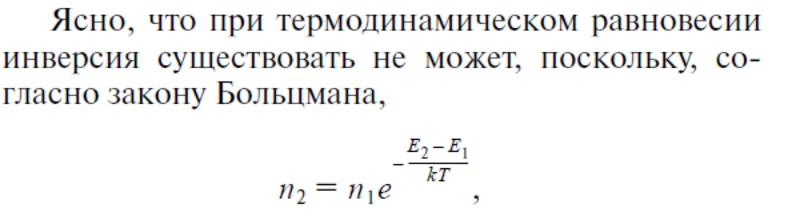
*Условие инверсной населенности в таком виде является необходимым и достаточным для непрерывной накачки. В импульсном режиме возможно кратковременное получение инверсии без выполнения указанного условия

Активное вещество содержит совокупность рабочих частиц - частиц определенного (одного и того же) сорта, обладающих подходящим спектром возможных внутренних энергий, соответствующих различным конфигурациям и состояниям содержащихся в них электронов. Такими частицами могут быть атомы, ионы, молекулы, дефекты кристаллических решеток и другие системы.

Взаимодействуя с внешним электромагнитным полем, рабочие частицы могут совершать переходы с одного уровня их внутренней энергии на другой, сопровождающиеся испусканием или поглощением кванта электромагнитной энергии. По этой причине будем именовать эти частицы также квантовыми.

Величины (уровни) возможных внутренних энергий квантовой частицы будем обозначать через (i = 1, 2, 3, ...), где индекс 1 соответствует самому низкому уровню энергии. Последующие уровни будем нумеровать возрастающими цифрами в соответствии с ростом их энергии. Нумерация уровней может начинаться и с другой цифры, например, с нуля. Будем пользоваться также понятием плотности населенности i-го уровня Оно выражает число рассматриваемых квантовых частиц, содержащихся в единице объема рабочего вещества, которые имеют энергию Статистический вес (статвес) уровня говорит о степени его вырождения.

Начнем с рассмотрения механизма перехода рабочего вещества в активное состояние на простейшей модели совокупности двухуровневых квантовых частиц, которая предполагает, что рабочие квантовые частицы имеют всего два уровня внутренней энергии В этом случае плотность числа частиц (число рабочих квантовых частиц в каждой единице объема рабочего вещества), или их концентрация N равна сумме плотностей населенностей этих двух уровней:

(1.1.1)

Плотность населенности уровня энергии совокупности рабочих частиц в случае, когда эта совокупность находится в состоянии термодинамического (теплового) равновесия, будем обозначать через В соответствии с формулой Больцмана

(1.1.2)

Здесь k - постоянная Больцмана, - постоянная Планка, - круговая частота квантового перехода между уровнями энергии частицы, удовлетворяющая соотношению

(1.1.3)

Т.к. то из (1.1.2) следует, что при термодинамическом равновесии а в случае, когда:

(1.1.4)

это означает, что

Пусть через рассматриваемое вещество распространяется монохроматическая электромагнитная волна, частота которой равна определяемой соотношением (1.1.3). Такую волну называют резонансной по отношению к данному веществу (данному переходу между уровнями энергии рабочей частицы).

При прохождении через рабочее вещество резонансная волна взаимодействует с ним, вызывая переходы рабочих частиц с одного уровня энергии на другой. Под воздействием кванта резонансного излучения каждая из рабочих частиц, будет иметь определенную вероятность, поглотив это квант, перейти на уровень если она находится на уровне или, если она находится на уровне перейти на уровень испустив при этом новый квант излучения, который невозможно отличить от кванта, вызвавшего этот переход. Как известно, первый из этих процессов называют поглощением, а второй - вынужденным испусканием излучения.

Для того, чтобы упростить дальнейшее рассмотрение, предположим, что статвеса уровней энергии и одинаковы, т.е. что В этом случае вероятности обоих процессов одинаковы. Число квантовых переходов в некотором (например, единичном) объеме рабочего вещества в единицу времени, соответствующее каждому из процессов, пропорционально плотности населенности начального уровня энергии перехода, т.е. для поглощения и для вынужденного испускания.

При термодинамическом равновесии и в этом случае величина энергии, теряемой электромагнитной волной из-за процесса поглощения, всегда превышает величину энергии, которая добавляется в волну из вещества за счет процесса вынужденного испускания. В результате интенсивность резонансного излучения при прохождении через равновесное вещество уменьшается.

Если же найти способ, позволяющий реализовать такое состояние рабочего вещества, в котором (это, собственно говоря, и является главной задачей при создании лазера), то процесс вынужденного испускания будет преобладать над процессом поглощения.

Если интенсивность волны резонансной частоты, проходящей через некоторое вещество, растет, то на языке классической электродинамики это означает, что волна усиливается. Усиление, которое основано на использовании процесса вынужденного испускания излучения, именуют квантовым. Отношение плотностей населенностей уровней энергии, участвующих в процессе квантового усиления, обратно по знаку существующему в рабочем веществе в случае термодинамического равновесия. Поэтому говорят, что в активном веществе имеет место инверсия населенностей уровней энергии рабочего квантового перехода.

Инверсная населенность и усиление света

Для усиления света при вынужденном излучении в активной среде должна быть создана инверсия населённостей. Если световое излучение является резонансным для двух невырожденных уровней, то преобладание вынужденного усиления над поглощением возможно лишь при выполнении условия:

>0, (3.1)

где , – населённости двух уровней. Населенность уровней, удовлетворяющая условию (2.1), называется инверсией населённостей. Если уровни состоят из вырожденных подуровней и энергии подуровней совпадают, то условие инверсии населенностей записывается в следующем виде:

>0, (3.2)

где , – степени вырождения двух уровней. Фактически условие (3.2) означает инверсию населенностей между парами подуровней уровней 2 и 1.

Если уровни и энергии подуровней не совпадают, то понятие условия инверсии населенностей становится не совсем корректным, т.к. и величина усиления и величина потерь оказываются спектрально зависимыми и, более того, зависят от температуры. В этом случае необходимо пользоваться общим выражением для инкремента усиления:

, (3.3)

где и – сечения поглощения и усиления (для рассматриваемого перехода) соответственно.

Следует отметить, что выражения (2.1) и (2.2) являются следствием выражения (2.3) для двух частных случаев: отсутствия вырождения и вырождения без расщепления энергий подуровней. В отсутствии разделения уровней на подуровни = , а в случае разделения на вырожденные подуровни без расщепления энергий подуровней = .

Инкремент усиления определяется как характеристиками перехода (сечениями поглощения и усиления) так и населенностями резонансных уровней. В отсутствие распределённых нерезонансных потерь в усиливающей среде интенсивность излучения растет экспоненциально:

, (3.4) где z – пройденное световой волной расстояние в активном веществе.

Сечение  действительно имеет размерность сечения [м2] или [см2]. Разность населённостей имеет размерность [см-3], коэффициент усиления - [см-1].

Принципы создания инверсной населённости.

Принципы создания инверсии населенностей:

1. Пространственная селекция возбужденных частиц

Если использовать поток частиц и пространственное разделение возбуждённых и невозбуждённых частиц, то в некоторой области можно получить среду с преобладанием возбуждённых частиц над невозбуждёнными.

На рис.1 показано пространственное разделение потоков частиц при поступлении потока частиц извне.

Рис.1. Пространственная селекция возбужденных частиц.

2. Быстрое изменение внешних условий – инвертирование энергетических уровней.

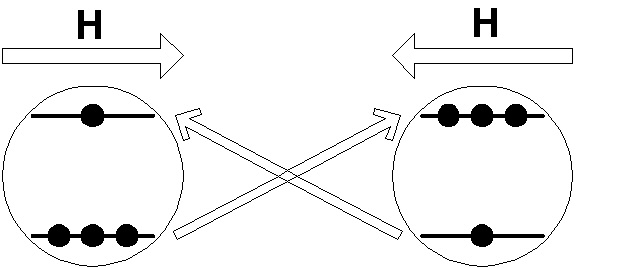
Рис.2. Быстрое изменение направления магнитного поля вызывает инвертирование энергии магнитных подуровней.

3. Использование верхнего вспомогательного уровня

В упрощённой модели квантовых частиц, обладающих всего двумя уровнями энергии, возбуждённая частица из состояния с энергией E2 может перейти в состояние E1 с испусканием фотона как самопроизвольно (спонтанное излучение), так и под действием резонансного излучения (индуцированное или вынужденное излучение). При условии термодинамического равновесия N2/g2-N1g1<0. Физически это объяснимо: поглощение света и вынужденное излучение – это процессы одной природы, и их вероятности одинаковы. Но к обеднению верхнего уровня (верхним называется уровень с большей энергией) приводит, также, спонтанное излучение. Вероятности процессов, связанных с вынужденными переходами 21 и 12 одинаковы не только для случая взаимодействия со светом, но и для процессов другой природы, например, акустических, химических процессов, возбуждения электронным ударом, при столкновениях и др.

Использование вспомогательного уровня позволяет получить населенность возбужденного уровня больше, чем населенность основного. Принцип использования верхнего вспомогательного уровня для получения инверсии населенностей поясняет рис.3.

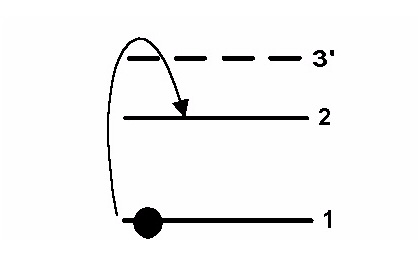
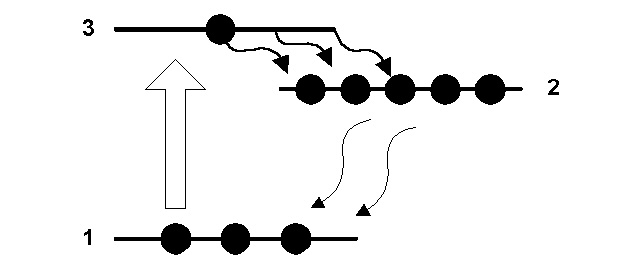
Рис.3. Принцип использования верхнего вспомогательного уровня для получения инверсии населенностей между уровнями 2-1 (слева) и его реализация при использовании селективной оптической накачки (справа).

Метод трех уровней был предложен Н. Г. Басовым и А. М. Прохоровым (1955 г.), предполагавшими использовать его уже при создании молекулярных генераторов. Идею метода иллюстрируют графические схемы, приведенные на рис. 6.3.1, где изображены уровни энергии трехуровневых рабочих частиц и Если совокупность таких рабочих частиц находится в термодинамическом равновесии с окружением-термостатом при температуре T, то соотношение плотностей населенностей уровней энергии и описывается формулой Больцмана (2.1.1):

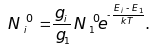(i = 2, 3). (6.3.1.1)

Упростим рассмотрение, положив Тогда:

(i = 2, 3). (6.3.1.2)

Рис. 6.3.1. Приближенная трехуровневая схема изменения плотностей населенностей рабочих частиц при включении накачки (в предположении, что величина при этом не меняется):

а) состояние термодинамического равновесия;

б) стационарное состояние при включенной накачке

На рис. 6.3.1 значениям плотностей населенностей соответствуют длины отрезков горизонтальных прямых на уровне соответствующих энергий.

Рис. 6.3.1 а иллюстрирует распределение плотностей населенностей при термодинамическом равновесии. В этом случае концы отрезков прямых, соответствующих величинам и лежат на изображенной на рисунке пунктиром больцмановской экспоненте, соответствующей выражению (6.3.1.2). Рис. 6.3.1.б показывает, как меняется ситуация под действием излучения накачки. Частота этого излучения является резонансной квантовому переходу т.е.:

(6.3.2)

Предположим, что интенсивность накачки достаточно велика и на переходе достигается практически полное насыщение: