3.3 Написание программы на машине Тьюринга
На рисунках 11 - 14 представлена написанная программа по ТСП.
Рисунок 11 – Работающая программа Тьюринга (Снимок 1)
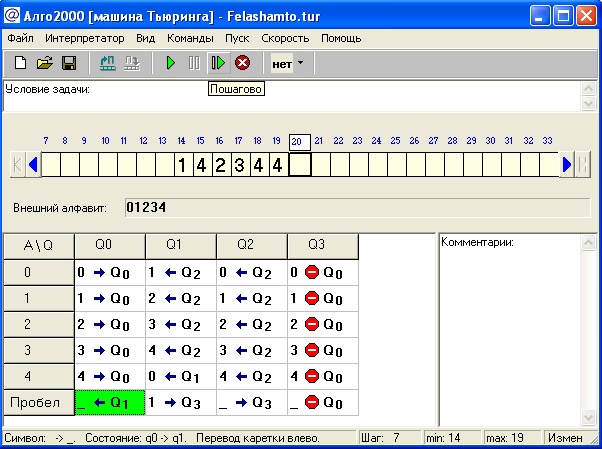
Рисунок 12 – Работающая программа Тьюринга (Снимок 2)
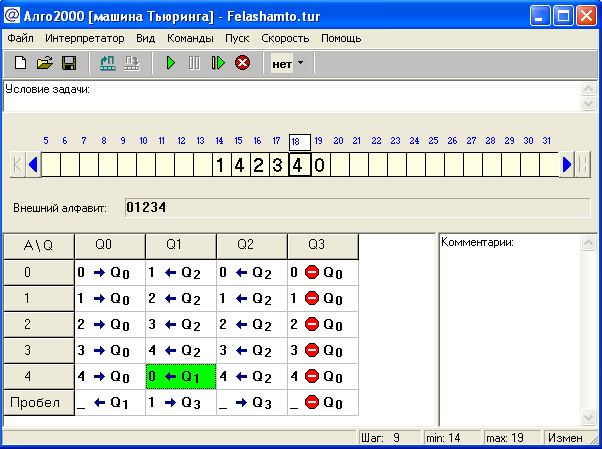
Рисунок 13 – Работающая программа Тьюринга (Снимок 3)
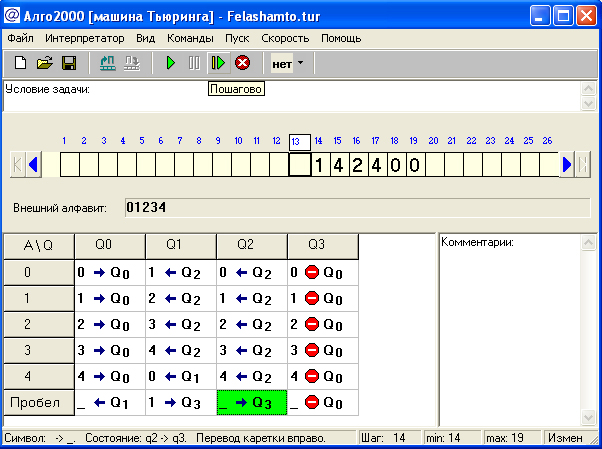
Рисунок 14 – Работающая программа Тьюринга (Снимок 4)
3.4 Анализ результата
Написанная программа позволяет увеличивать введенное число на единицу, согласно правилам счисления пятеричной системы. Несмотря на то, что программа запускается из стандартной позиции и возвращается к ней же, программа может быть запущена и из другого состояния, когда каретка расположена над числом.
Т.к. исходное и конечное состояние совпадают, путём многократного последовательного запуска возможно использовать её, как счётчик в 5чной системе счисления, автоматизировав процесс запуска программы.
В
ЫВОД
Поставленные задачи курсовой работы были выполнены полностью. Была решена задача на примитивную рекурсию, спроектированы и написаны программы: умножения на три для машины Поста и программа счёта в 5ий системе счисления для машины Тьюринга.
Машины работают исправно. выполняют свои функции полностью.
Список литературы
Ершов, С. С. Элементы теории алгоритмов: учебное пособие/ С. С. Ершов. — Челябинск: Изд-во ЮУрГУ, 2009. — 64 с.
Ершов С.С., Надточий И.Л., Самохвалов А.В. Прикладная математика: Учебное пособие по практическим занятиям. – Челябинский ЧТУ, 1992. – 85с.
СТО ЮУрГУ 04–2008 Стандарт организации. Курсовое и дипломное проекти-рование. Общие требования к содержанию и оформлению / составители: Т.И. Парубочая, Н.В. Сырейщикова, В.И. Гузеев, Л.В. Винокурова. – Челябинск: Изд-во ЮУрГУ, 2008. – 56 с.