7.Фрикционные передачи и вариаторы. Кинематика передач. Точность передаточного отношения. Потери на трение. Кпд.

Фрикционной передачей называется механизм, служащий для передачи вращательного движения от одного вала к другому с помощью сил трения, возникающих между насаженными на валы и прижатыми друг к другу дисками, цилиндрами или конусами. Фрикционные передачи относятся к передачам с непосредственным контактом. Их работа основана на принципе использования силы трения. К ним относятся вариаторы, отличающиеся простотой конструкции, позволяющие легко обеспечить бесступенчатое регу¬лирование частоты вращения ведомого вала. Передача вращающего момента в вариаторах осуществляется либо за счет силы трения (фрикционные вариаторы), либо за счет зацепления рабочих эле¬ментов (цепные вариаторы).

Фрикционные передачи можно классифицировать по нескольким признакам:

1)по расположению осей валов, по форме тел качения, по условиям работы;

2) по возможности регулирования передаточного числа

В результате неизбежного при работе фрикционных передач упругого скольжения ведомый каток отстаёт от ведущего и точное значение передаточного числа будет определяться по формуле

i=w1\w2=D1\D1(1- )

где - коэффициент скольжения

Наличие упругого скольжения и некоторая его зависимость от колебаний нагрузки и условий работы передачи вынуждают называть передаточное число фрикционной передачи условно постоянным. Для практических расчётов силовых фрикционных передач пользуются приближённым значением передаточного числа i=D1\D2

8.Ременные передачи. Осн характеристики. Геометрические зависимости.

1. простота изготовления

2. лучшая вибро-пассивность

3. малый шум

4. могут служить предохранительным звеном

5. допускают бесступенчатое регулирование

6. обладают хорошими амортизирующими и демфирующими свойствами

7. возможность больших межосевых растояний

8. универсальность расположения валов и их количество в передаче

9. может одновременно выполнять функции муфты сцепления.

-

1. большие габариты

2. малый КПД

3. малая долговечность

4. большие эксплуатационные расходы

5. непостоянство передаточного отношения.

Виды ременных передач

Относятся к передачи трением с гибкой связью. Состоит из 2-х или более шкивов и гибкой связи. Гибкой связью служит ремень прямоугольного, трапециидального или круглого сечения.

Различают виды ременных передач:

1. плоскоременные

2. клиноременные

3. многоклиновые

4. поликлиновые

5. круглоременные

Типы ременных передач

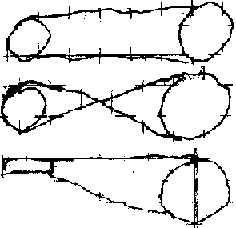
1. Открытая

2. Перекрестная

3. Полуперекрестная

Геометрия клиноременной передачи

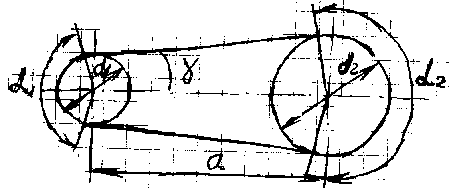
d₁, d₂ – диаметры ведущего и ведомого шкивов, £­₁, £₂ – углы обхвата на шкивах,  – угол наклона ветви ремня к оси центра, а – межосевое расстояние.

£_1,2 = 180  2, «+» для большего, «–» для меньшего.  = arcsin[(d­₂ – d₁) / 2a]

a_min =0,55 (d₂+d₁)+h, где h – высота сечения ремня

a_max = 2(d₂+d₁)

9.Силы и напряжения в ременной передаче. Критерии работоспособности и расчета ременных передач.

Силы и напряжения в ремне

1. Силы растяжения F₁ и F₂

2. Напряжение изгиба на шкивах (на ведомом меньше)

3. Напряжение, вызываемое силой предварительного натяжения F₀= F_t = 2T₁ / d₁, ₀ = F₀ / A. Для плоскоременной передачи A = b  , для клиноременной A = A₁ z, где b – ширина ремня,  – его толщина, A₁ – площадь сечения 1-го клиноременного ремня, z – число ремней

4. На холостом валу возникает центробежная сила F_Ц =   A  V², где  – плотность, A – площадь, V – скорость.

5. Напряжение, вызываемое центробежной силой _Ц = F_Ц / A= V².

Критерий работоспособности ременной передачи

Работоспособность ременной передачи может ограничиваться:

1. сцеплением ремня со шкивами (тяговая способность)

2. долговечность ремня

Тяговая способность зависит от предварительного натяжения F₀ или ₀, а также от материала ремня, угла обхвата, диаметра шкивов,

Долговечность ремня зависит от сопротивления усталости его элементов

^P_max  N_E = const, где p – степень кривой усталости, p = 11 для клиноременной, p = 6 для плоскоременной.

N_E = 3600  U  Z_m  L_h / _ИЗГ

U – частота пробега ремня

Z_m – число шкивов

_ИЗГ – коэффициент, учитывающий разую степень изгиба на большом и малом шкивах,

L_h – ресурс работы

Расчет ременных передач

Расчет производится по полезному напряжению или эталону мощности

K = F_t / (A₁  z) < [K] или p = KAV/1000

A₁ – площадь поперечного сечения одного ремня, z – число ремней

[K] = K₀  C_£  C_P, где K₀ – определяется из условия обеспечения тяговой способности при оптимальном коэффициенте тяги ₀ и долговечности N_E или L_h

С_£ – угол обхвата

С_P – режим работы

, где С – показат. долговеч.

За базу выбирается эталонная передача с двумя шкивами с передаточном числом 1,  = 180. Ремнем эталонной длины и имеющего эталонную скорость V при ресурсе работы L_h = 25 тыс. часов, работа спокойная, запас сцепления  = 1, 5.

Необходимое число ремней определяется по формуле z = F_t / ([K]  A₁)

10. усилия в зацеплении прямозубой цилиндрической передачи. Повреждения зубьев.

Силы в зацеплении определяют в полюсе зацепления. На шестерню действует вращательный момент, который создаёт распределённую по контактным линиям зуба колеса нагрузку. Эту нагрузку заменяют равнодействующей силой , направленной по линии зацепления nn и приложенной в полюсе. Силами трения в зацеплении пренебрегают, так как они малы. Силу раскладывают на окружную Ft и радиальную Fr (рис. 2.3.12):

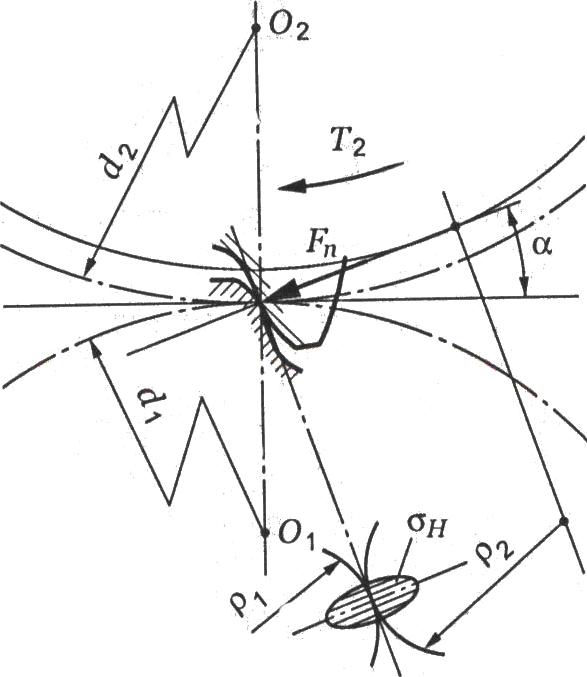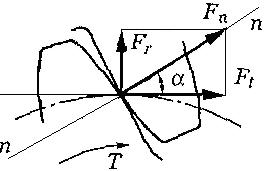; Рисунок 2.3.12 Схема действия сил в зубчатом зацеплении

(2.3.14) (2.3.15)

Такое разложение силы Fn на составляющие удобно для расчёта зубьев и валов. На ведомом колесе направление силы Ft совпадает с направлением вращения, а на ведущем – противоположно ему, т.е. силы на ведущем и ведомом колёсах всегда направлены против действия соответствующих моментов. Радиальные силы Fr направлены к осям вращения колёс и создают «распор» в передаче. Расчет на прочность зубчатых колес проводят по двум условиям прочности: по контактным напряжениям и по напряжениям изгиба. При расчете по контактным напряжениям для всех коэффициентов применяется индекс «Н», по напряжениям изгиба – индекс «F».

Виды разрушений зубьев и виды расчетов

1) Излом зуба (изгиб зуба)

а) мгновенный излом от нарушения статической прочности при значительных нагрузках

б) усталостный излом в результате многократного изгиба зуба.

2) разрушение рабочей поверхности в виде:

а) абразивный износ

б) заедание и волочение из-за отсутствия смазки или недостаточной вязкости

в) выкрашивание – появление и развитие усталостных трещин на поверхности. При этом повышаются контактные напряжения.

г) смятие поверхности.

Наиболее опасным является уставлостный излом и усталостное выкрашивание, другие виды разрушение можно избежать конструктивно.

Выводы: закрытая передача на заданный срок службы должна быть рассчитана на сопротивление контактной усталости _H и проверена на сопротивление по изгибу _F. Для открытых передача на заданный срок службы рассчитывается изгиб и проверяются на сопротивление контактной выносливости.

11. Геометрия и кинематика косозубых цилиндрических передач

Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном диаметре, называют косозубыми. При работе такой передачи зубья входят в зацепление не сразу по всей длине, как в прямозубой, а постепенно; передаваемая нагрузка распределяется на несколько зубьев. В результате по сравнению с прямозубой повышается нагрузочная способность, увеличивается плавность работы передачи и уменьшается шум. Поэтому косозубые передачи имеют преимущественное распространение. С увеличением угла наклона линии зуба плавность зацепления и нагрузочная способность передачи увеличиваются рис.2.3.15, но при этом увеличивается и осевая сила Fа, что нежелательно. Поэтому в косозубых передачах принимают угол .Основные геометрические размеры зависят от модуля и числа зубьев. При расчёте косозубых колёс учитывают два шага: нормальный шаг зубьев pn - в нормальном сечении, окружной шаг pt – в торцовом сечении; при этом Соответственно шагам имеем два модуля зубьев:

(2.3.22) (2.3.23) при этом (2.3.24)

где mt и mn – окружной и нормальный модули зубьев.

12.Силы в зацеплении определяют в полюсе зацепления. Сила , действующая на зуб косозубого колеса рис. 2.3.16, направлена по нормали к профилю зуба, т.е. по линии зацепления эквивалентного прямозубого колеса и составляет угол с касательной к эллипсу.

Разложим эту силу на две составляющие: окружную силу на эквивалентном колесе: (2.3.22) радиальную силу на этом колесе: (2.3.33) Переходя от эквивалентного к косозубому колесу, заметим, что сила является радиальной силой и для этого колеса, т.е.

сила Ft расположена в плоскости, касательной к начальному цилиндру, и составляет угол с осью колеса. Разложим силу Ft на две составляющие: окружную силу (2.3.35), и осевую силу (2.3.36). Окружная сила известна. Её определяют по передаваемому моменту и диаметру делительной окружности зубчатого колеса (2.3.37) Тогда из формулы (2.3.35): следует Подставив силу и выражения , окончательно получим: радиальную силу

и осевую силу

На зубья шестерни и колеса действуют одинаковые, но противоположно направленные силы. При определении их направления учитывают направление вращения колёс и направление наклона линии зубьев (правое и левое). Наличие в зацеплении осевой силы, которая дополнительно нагружает валы и подшипники, является недостатком косозубых передач.