2. Для представления целых чисел со знаком старший (левый) разряд отводится под знак числа. Если число положительное, то в знаковый раз­ряд записывается 0, если число отрицательное, то — 1.

Максимальное значение целого числа со знаком достигается в случае, когда в старшем разряде стоит 0, а во всех остальных ячейках стоят еди­ницы. Если под представление целого числа со знаком отведено N бит, то максимальное значение будет равно 2^N-1-1. Поскольку количество возможных значений в N битах равно 2^N-1, то в случае представления целых чисел со знаком количество отрицательных значений на единицу больше количества положительных значений. Такая ситуация связана с тем, что для представления нуля во всех ячейках стоят нули. Если же в знаковом разряде стоит единица, а во всех остальных разрядах нули, то это представление соответствует отрицательному (как правило, наимень­шему) числу.

Пример. Запишем вид числа -58 в памяти компьютера в 8-разрядном представлении.

Так как 58₁₀ = 111010₂, то число в памяти компьютера будет пред­ставлено следующим образом:

1

0

1

1

1

0

1

0

Представление в памяти компьютера целых положительных чисел совпадает с прямым кодом.

Система счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков.

Система счисления:

• даёт представления множества чисел (целых и/или вещественных);

• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление);

• отражает алгебраическую и арифметическую структуру чисел.

Системы счисления подразделяются на позиционные, непозиционные и смешанные.

-Позиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака(цифры) в записи числа зависит от его позиции (разряда).

-Смешанная система счисления является обобщением  -ричной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел  , и каждое число   в ней представляется как линейная комбинация:

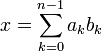, где на коэффициенты  , называемые как и прежде цифрами, накладываются некоторые ограничения.

-В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.

Арифметические операции в различных системах счисления

Производятся по тем же правилам, что и в десятичной с.ч.

если результат поразрядного сложения в каждом разряде меньше основания системы счисления, т.е.

аi + bi, < р,

то в соответствующий разряд суммы записывается цифра, которая отображает количество, равное ci = ai + bi

В том случае, если результат поразрядного сложения больше ос­нования системы счисления или равен ему, т.е.

аi + bi,  р,  то в соответствующий разряд суммы записывается цифра, которая отображает количество, равное:

Ci = ai + bi - p

и в старший разряд c1+i переносится единица, которая должна учи­тываться при суммировании в этом разряде. При вычитании поступают по аналогичным правилам.

Пример 1. Сложим числа 15 и 6 в различных системах счисления

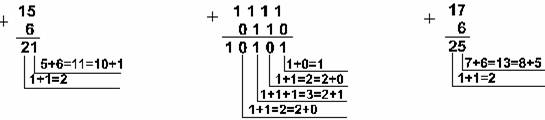
Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆

Шестнадцатеричная: F₁₆+6₁₆

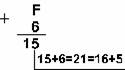       Проверка. Преобразуем полученные суммы к десятичному виду: 10101₂ = 2⁴ + 2² + 2⁰ = 16+4+1=21,  25₈ = 2*8¹ + 5*8⁰ = 16 + 5 = 21,  15₁₆ = 1*16₁ + 5*16₀ = 16+5 = 21.

Пример: Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

Проверка. Преобразуем полученные суммы к десятичному виду:  11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25  311,2₈ = 3*8² + 1•8¹ + 1*8⁰ + 2*8^-1 = 201,25  C9,4₁₆ = 12*16¹ + 9*16⁰ + 4*16^-1 = 201,25