Глава 3

Разрешение парадокса. Численный эксперимент. Предельное автомодельное решение

Таким образом, продвигаясь по традиционному пути, попадаем в парадоксальную ситуацию: отработанная ранее схема анализа размерностей и построения автомодельного решения в данном (и вроде бы - аналогичном) случае не срабатывает.

Для того, чтобы выйти из создавшегося тупика и разобраться, что же происходит “на самом деле”, приходится решать задачу “в лоб”, то есть численно решать исходную задачу (??). Такие решения были проведены для различных е = к₁/к и различных начальных условий типа (рис. ??)

u(x, 0) = 10; — 0,1 < x < 0,1 u(x, 0) = 0; 0,1 < |x| < то

При этом оказалось, что закон затухания возмущения в точке источника (то есть максимального возмущения) u(0,t) = u_m имеет вид, представленный на рис. ??, откуда можно заключить, что, спустя

Рис. 3.1: Начальное условие типа “численной” 5-функция и его эволюция во времени при численных расчетах

некоторое время после начала численного счета, хорошо выполняется соотношение

ln u_m = k ln t + b

где k = const, b = const, или, в более удобной для дальнейшего анализа форме

ln u_m = —¹ + ^а ln(Kt) + ln A ^ u_m = A/(Kt) +

2

Расчеты показали, что A = А(н.у.), а а = а(е). Если теперь в качестве временизависимых масштабов взять для изменения линейных размеров x₀(t) = л/Kt, а для амплитуды давления (температуры) u₀(t) = A/(Kt) — и построить графики зависимости u/u₀ = f (x/x₀) различHbixt, то спустя некоторое время после начала

t

на некую асимптотику, которую естественно назвать “автомодельной промежуточной асимптотикой”, поскольку данная зависимость получена

Рис. 3.2: Закон затухания u (0,t)

Рис. 3.3: Эволюция зависимости u/u₀ = f (x/x₀, t)

х/

в указанных выше временизависимых масштабах

A( ) x ^u(x^Г) = 1_+а(_£) ^Ф(-j=, е) 3.1)

(кг) -2- V«t

Таким образом, вместо предполагаемого из проведенного в предыдущей главе анализа размерностей вида промежуточной автомодельной асимптотики

^u = -7= ^Ф(£,^⁾ (3-2)

л/кГ

получаем асимптотику другого вида

^A ч ^{A/Q Q} />- Ч

^u = / ^Ф(£, ^г) = TZfW ^{Ф (£}, ^£) ,

(кГ) 2 (кГ) ² V кГ

где A = А(н.у.); а = а(е)

К форме (??) анализ размерностей приводит, если отталкиваться от н.у., которые имеют предельный характер, т.е. есть от н.у. для точечного источника, который формально описывается обобщенной функцией 6 (x).

Но в нашем численном эксперименте 6-функция в чистом (аналитическом) виде не может быть использована. В этом случае приходится использовать обычные функции (типа представленной на рис.

??), которые должны количественно описывать н.у., т.е. удовлетворять условию

С Ю

Q = u(x, 0) dx

J —Ю

При этом они неизбежно отражают наличие собственного характерного пространственного масштаба задачи ~ l (смотри рис. ??). Наличие данного масштаба — конечного размера области впрыска или удаления t=0

обычного автомодельного решения.

Используя для обезразмеривания этот масштаб, получим, что в общем случае

/ гл ^Q 0/^x\ ^{u(x, 0)} = y^{u (}у⁾

где вместо переменного масштаба \/Kt использован постоянный (собственный) l.

f u(x, 0) dx = f ^Qu⁰(^x) dx = Q f u⁰(^x) d(^x) = Q

7^—то 7^—то l l 7^—то l l

следовательно

/“ u⁰(Z) dZ = 1

J —то

где Z = x/l.

Очевидно, что u⁰(Z) - безразмерная, четная, финитная функция. При таких условиях на u⁰(Z), фигурирующую в начальных условиях, решение задачи Коши существует (что устанавливается соответствующей теоремой), но в общем случае оно неавтомодельно.

При этом из стандартного анализа размерностей имеем

^Q гр(с \ С ^{x l К}1

= -Kt^{F(£,п,е); £} = -Kt^{; п} = —t^{; е} =

Рассмотрим далее предел функции F(£, п, е) при п, стремящейся к нулю. В случае е = 1 имеем обычную немодифицированную задачу, когда характеристики среды не меняются. При этом величина п ^ 0 либо при

50. ^ 0, либо при t ^ то, так как (l = const). Таким образом, можно выбрать такой характер стремления x ^ то, чтобы £ = const, но при этом п ^ 0, тогда в пределе получим известное автомодельное решение для задачи о мгновенном источнике

u = ~7=/ (£, 0,1) = -'jLf (£) (3.3)

у Kt у Kt

Соотношение (??) - это асимптотика широкого класса начальных задач при больших временах, когда размер источника перестает сказываться.

Для исследуемой модифицированной задачи, когда £ = 1, при п — 0 предполагалось существование

Hm F^(£,п^,е = ¹⁾ = ^ф(£,£)

п——0

где функция Ф(£,г) есть просто функция не одного, а двух переменных, но, как показано в главе 4, такого предела не существует. В то же время из численных расчетов мы получили некоторую асимптотику, правда в другой форме

u = ^A/QQ “т= Ф(£, £) (3-4)

(Kt) 2 y/Kt

Исходя из структуры параметра п = I/л/Kt, легко выделить его из “дополнительного” коэффициента в формуле (??)

A/Q l^a A l^a A _{a B a}

(Ktjf ¥ = Qia (Kt)f = Qaⁿ = ^Bn

где A, Q, l, а и, соответственно, B - некоторые константы.

u

функциональной зависимостью

u = B -^L п^аФ(£,£) = [n^af (£,£) + o(n^a)]

у Kt у Kt

Слагаемое о(п^а) появляется в связи с тем, что речь идет об асимптотическом представлении, то есть если lim F(£,п,£ = 1) существует, то, очевидно, справедливо асимптотическое представление

^{F (}^ П^,£ = ¹⁾ = п^{а f (£, £)} + ^о(п^а)

При указанном предельном переходе предельное автомодельное решение представляется в виде (??), получаемом в численном эксперименте

60

^u = -Т=П“/^{(£ г)} = , ^Q,^l1+a ^{f (£ г)} = ₍ fl+a ^{Ф(£ г)} (3-5) л/кГ (кГ) 2 (кГ) 2

где A = 7 iim Ql^a = const, a 7 - безразмерная константа, зависящая от

нормировки Ф(£, г) при переходе к функции Ф(£, г) от функции f (£,г).

Следовательно, в данной задаче появляется инвариант

Ql^a = const

Это означает, что задачи, в которых сами величины Q,U а имеют различные значения, в случае совпадения значений такого инварианта будут иметь одинаковые решения.

а

например, выполняя численно предельный переход от решения неавтомодельной задачи к предельной автомодельной асимптотике.

Но важно подчеркнуть, что в любом случае определение

а

процесса определения предельного автомодельного решения.

С учетом проведенного анализа, приводящего к принципиально новому виду асимптотического представления автомодельного решения в виде (??), или (??), или (??), схема (алгоритм) получения аналитического решения выглядит следующим образом:

1. Подставляя (??) в (??), получаем для Ф(£,г) обыкновенное дифференциальное уравнение второго порядка с разрывным коэффициентом при старшей производной

гФ" + (£/2)Ф' + [(1 + а)/2]Ф = 0; 0 < £ < £о

(3.6)

Ф" + (£/2)Ф' + [(1 + а)/2]Ф = 0; £о < £ < ю

Разрыв указанного коэффициента происходит в точке £0, где d_tu =

0

координата £₀ разрыва коэффициента при Ф" неизвестна и ищется в ходе решения) задача на собственные значения.

Дополнительные условия, необходимые для получения конкретного вида решения задачи (??), возникают из следующих соображений

1. . В силу естественной симметрии задачи

Ф'(0,е) = 0 (3.7)

2. . Условие нормировки функции Ф(£, е) естественно задать

в виде

Ф(0, е) = 1 (3.8)

что в размерных переменных будет соответствовать выполнению соотношения

u(0,t) = A(Kt)^—(1+^a)/2

3. . Естественно потребовать также непрерывности получаемого решения

Ф(£0 — 0,е) = Ф(£0 + 0, е) (3.9)

4. . Учитывая, что d_tu д2_х u ~ Ф", откуда Ф"(£₀,е) = 0, получаем при £ = £₀ условие

&Ф'(£0,е) + (1 + а)Ф(£0,е) = 0 (3.10)

5. . И, наконец, из соображений выполнения закона сохранения (энергии или массы) должно выполняться соотношение

/СЮ

|£|“Ф(£,е) d£< то 3.11

-сю

гж I—ос

t

l

udx < ж(= 0)

u

lx

возмущения) размерами источника, из последнего неравенства как раз и получаем условие (??).

Математическая теория обыкновенных

дифференциальных уравнений второго порядка в настоящее время развита чрезвычайно сильно, что позволяет получать аналитические решения для очень широкого спектра таких уравнений. Выписываем

решение системы (??) при условиях

(3.12)

^ф = Сехр( 8_ ^)[D_a^(—2_⁾ + ^D_a⁽JL^{)]; 0} < ^£ < ^£0

^ф = ^Fехр⁽ =f^)Da⁽-2⁾; ^£0 <^£< ^ж

где D_a (z) - функция параболического цилиндра* (функция Вебера или Вебера-Эрмита).

Условие (??) используется для получения решения в области 0 < £ < £₀, а условие (??) - в области £₀ < £ < ж. Из условия

С

1а

¹⁺п

/2

(3.13)

= Г

2Da(0)

С=

1

где Г (•) — 7-функция, а из условия непрерывности (??) функции Ф(£, е)

'А'

,-2,

'Jg_

,-2_;

'—о' —2е

1

(3.14)

D

Da

+ ^Da

£/

£0 F

' £2(1 — е^—1)

F = С ехр

8

2. Для определения зависимостей а (г) и £о(г) обратимся к условию (??)• Используя при этом рекуррентные соотношения для производных функций Вебера - Эрмита и выражение этих функций через вырожденные гипергеометричесие функции* , получаем систему трансцендентных уравнений

3.15)

J Да₊2( -2) = ⁰

1. ^M (—г — 1 2^, § ) = ⁰

а

u = —4+^-Ф(£,г) удовлетворяет уравнению (??) и всем поставленным

(Kt)

условпям.

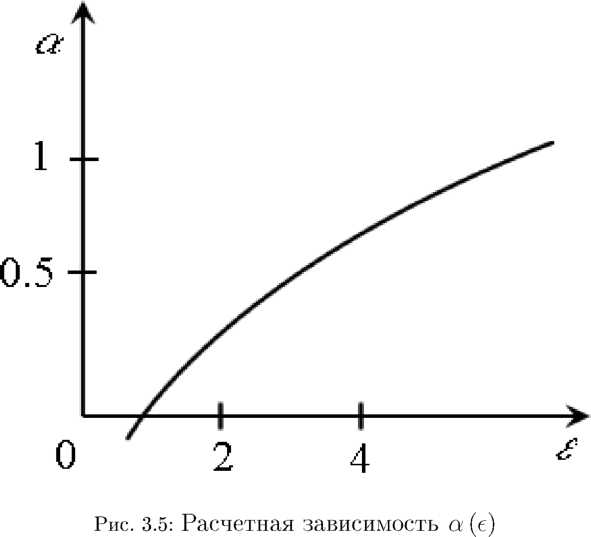
На рис.?? приведен пример графического решения системы (??). Кривая 1 на графике представляет собой решение первого из уравнений системы относительно £/л/2 в функции пара метра а. Кривая

2. есть решение второго уравнения системы относительно £/л/2ё (в рассматриваемом примере г = 2).

г

а

кривых 1 и 2). Результат такого варьирования приведен на рис.??. Таким

г

а, что позволяет выписать решение задачи в виде (??), где Ф(£,г)

^£о

на рис.??.

Полученное таким образом предельное автомодельное решение уже не представляет собой обычное автомодельное решение задачи о мгновенном точечном источнике: наличие характерного размера

50. 

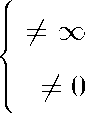
    2 s?o I

    Рис. 3.4: Графическое решение системы трансцендентных уравнений

    О 1 2

    приводит к появлению инварианта Ql^a = const. Поэтому асимптотика решения для t ^ то будет одна и та же для различных Q и l, необходимо лишь сохранение инварианта Ql^a. При этом можно сформулировать следующий “эмпирический” вывод: в соответствии с практикой численного анализа поведения предельного автомодельного решения, в случае начального условия, описываемого обычными функциями вида u(x, 0) = (Q/l) u⁰ (ж/l), где явно присутствует характерный масштаб задачи l, существует такое число а, что

lino n ^aF⁽С^,п^,£⁾ = f ⁽С^,£⁾

Но строго эта теорема пока не доказана.