Глава 7 177

^2(ui ^{- u}2⁾q% = \13^^(ui ^{- u}2⁾q^2(ui ^{- u}2^{)(1 -} q^2)(ui ^{- и}3^{) 1 -} q²S-2 187

= j^(ui ^{- u}3^{)/3a(1 -} q²⁾ (^{1 -} q²) ^(ui ^{- u}2⁾q 187

Понятие о локализации тепла и граничных режимах с обострением 200

Понятие о фракталах и фрактальной размерности. Самоподобные кривые 226

К у 266

^А Нл(М/ К \ 296

Окончательно, возвращаясь к размерным переменным, получаем решение, описывающее П-ю промежуточную стадию процесса

₂

Mx

u = 5777 exp

2/Л[к(( — to )]^3/2

_x2

(1.17)

4«(t — to)

Для определения временного интервала его справедливости

^to

t

превышающее время to, так что t₀/t ^ 1. В этом случае

g—x²/4«(t—to) = g—x²/4«t(1—to/t) ^ g(—x²/4Kt)(1+to/t) C"U g—x²/4Kt

а

1

t^—3/2 (1 — t₀/t) ^3/2 = t^—3/2

3/2

^{(t — t}0⁾

^3t0 3 • ⁵ /^t^²

¹⁺2t ^— Ail 7j +

3t₀ t²

0

= t^—3/2 1 + 3t° + O

2t / \t⁷/²_/

Тогда, с точностью до малых добавков более высокого порядка малости по t₀/t ^ 1, функцию и можно записать в виде

_х²

Mxe ^4Kt Л 3t0 \ ₍ ,

^{u и} I¹ + а) ⁽¹'¹⁸⁾

С другой стороны, решение для случая сосредоточенного источника в полубесконечном стержне можно представить как интерференцию решений для 2-х сосредоточенных источников (положительного и отрицательного) на бесконечном стержне, расположенных симметрично относительно начала координат (см. рис. ??).

Поскольку решение задачи для распространения возмущения от сосредоточенного источника по бесконечному стержню уже получено выше (??), воспользуемся им — в результате получаем

^(x-xo^{)2 (x}+^xo⁾²

(1.19)

4 Kt — e 4 Kt

Q и =

2. \/nKt

В соответствии с использованным при получении первого варианта асимптотического выражения для и(х, t) (??) условием t₀/t ^

1. рассмотрим большие рас стояния х ~ 2\/к£, когда х₀/х ^ 1. В этом случае можно пренебречь членами х0 в показателях экспонент, считая,

ЧТО

(х — х₀)² = х² — 2хх₀; (х + х₀)² = х² + 2хх₀

42

Рис. 1.3: Бесконечный стержень (II) с симметричной системой “источник- антиисточник" эквивалентен иолубесконечному стержню (I) с одним источником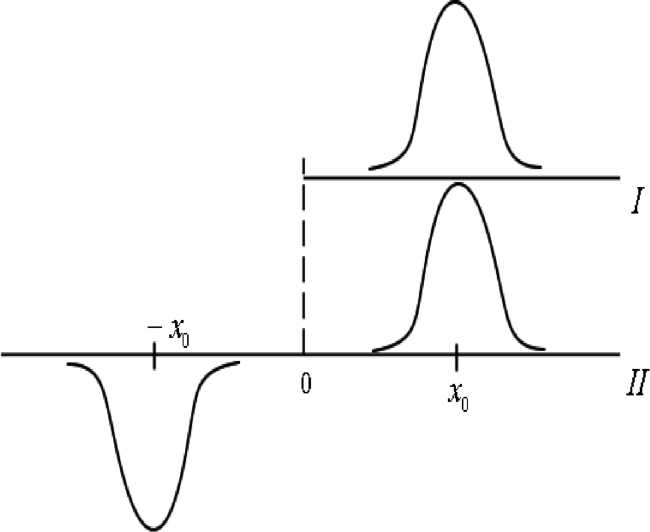

Тогда экспоненты соотношения (??) примут вид

2

2

x² — 2xxo

2

2

o

X'X

o

X

X

4«t

4«t

= e ^4Kt •

4«t

e

= e

e

e

x +2xxo

e ^4Kt

Введем для удобства обозначение а = хК+ ^и представим выражение в квадратных скобках соотношения (??) таким образом

2

2

e ^4Kt (e^a — e ^a) = 2e ^4Kt sh a

Из принятых условий (x — 2\/Kt, x₀/x ^ 1) вытекает условиe для a:

a ^ 1. Учитывая его, оставим в разложении гиперболического синуса

. а³ а⁵

sh а = а + — + 77 + • • •

3! 5!

только два первых слагаемых. Представим их, с учетом условия x — 4^t, в виде

2а + 3! а —

+

+

Kt 6(Kt)

Kt 3 • 8(Kt) Kt 6(Kt) 4к£

-1

₃ xx₀ x x₀ xx₀ xx₀ x xx₀ xx₀

+

Следовательно, асимптотическое представление поведения функции u(x,t), полученное в рамках проведенного рассмотрения, есть

u « ^Q _1/2 e ^4К • Г2а + ^а³) =

2(nKt)^1/2 V 3! )

2УП (Kt)^3/2

Сопоставим асимптотики (??) и (??), полученные для больших времен и расстояний, то есть вдали от источника. Очевидно, они должны совпадать, откуда следует, что

^{3 t}0 = ^x2 _t = ^x0 (л ₉₁n

2 ' t = 6(Kt) ^ ⁰ = 9к ^{( }}

Полученный результат - to ~ 0, 1x0/k - по порядку величины совпадает со временем окончания первой (“бесконечной”) фазы t*, и в этом смысле указанные времена можно отождествить (t* = ^t0

Хотя более точные выражения (??) и (??) для этих времен указывают на существование некоторого (хоть и кратковременного) переходного периода между I-й и 11-й рассмотренными фазами, поскольку t₀ = 2t*.

В заключение анализа второй фазы распространения возмущения от источника найдем сечение x = x*(t), где на данной стадии реализуется максимальная амплитуда возмущения (т.е. функции u) — u_m. Для этого, как обычно, воспользуемся условием равенства нулю производной в точке экстремума функции (в нашем случае - максимума

Mxe

e ⁴«i =

6(Kt)

d_xu(x = x*) = 0 (1.22)

Подставляя (??) в условие (??), получаем

M x² Mx 2x x²

-e ^4K(t-to⁾ e ^4K(t-to⁾ = 0

2^n[«(t — to)]^3/2 2^n [K(t — to )]^{3/2 4K(t — t}o⁾

₂

1+ ^x°

^Q

/у»

(Л/ 0 *АУ *АУ 0

(1.20)

1/2

Kt 6(Kt)²

2(nKt)

Данное равенство выполняется в двух случаях: когда

t — t0 — 0

что отражает тот очевидный факт, что максимум функции и имеет место в начальный момент времени t = t₀, с которого начинается рассмотрение

^х0

и когда

_2х²

1

1

4«(t —10)

= 1- -С² = 1- С² = 2

K(t — t0)y ^; 2^{С ; С}

х

2

то есть

или в размерных переменных

х*^) = ^/2«(t — t0)

Таким образом при t > t₀ максимум и находится в подвижной точке, а его величина есть

Mx*(t)

^Um —

|x*(t)]² e ^4K(t-to⁾ =

2^i[_K(t —10)]^3/2

M

Me^—1/2

• e^—1/2 =

^\/nK(t — t0) ~ \/2nK(t — t₀) 4«(t — t0) (1-23)

Если теперь построить график функции (??), используя в качестве масштабов (единиц измерения): для величиныu₀ = _4к(М—_to) ? ^а Д^ля расстояния х₀ = ^2K(t — t₀), получим самоподобную кривую (рис. ??), которая представляет собой профиль распределения u(x) в указанных единицах измерения для любого момента времени.

Итак, проведенное рассмотрение позволило получить в некотором интервале времени аналитическое решение задачи в виде

А	и
ш	1 \ 1 \
	1 1 \ 1 \ 1 \
	1 \ 1 1 , ,—	■124-t,

Рис. 1.4: Самоподобный профиль распределения u(x) на II стадии процесса

В.В. Кадет Прикладные задачи математической физики. 1

В.В. Кадет Прикладные задачи математической физики. 2

Оглавление 4

Предисловие 9

Введение. Анализ размерностей и подобие 12

[и] — [ДТ] — [Q] • L^-3 32

Задача о мгновенном точечном источнике на конечном линейном отрезке 42

= t^—3/2 1 + 3t° + O 65

Q и = 67

Задача о мгновенном источнике в нелинейной среде 85

дм 90

к 90

d² к₁ d² d² 90

Разрешение парадокса. Численный эксперимент. Предельное автомодельное решение 95

Полная и неполная автомодельность. Автомодельные решения первого и второго рода 115

Решения типа бегущих волн. Их связь с автомодельными решениями 126

Сильные фильтрационные и тепловые волны 144