Глава 12 Задача о расплывании бугра подземных вод

Рассмотрим характерную для подземной гидромеханики задачу о движении в пласте, изолированном с подошвы, воды, первоначально локализованной в ограниченной области — например, в результате кратковременной закачки . Это так называемая задача о расплывании бугра подземных вод, схема которой представлена на рис. 12.1 .

1. Постановка задачи

Течение при этом является безнапорным, то есть растекание воды по непроницаемому основанию происходит только под действием гравитационной силы. Поскольку фильтрационное течение весьма медленное, пренебрежем скоростным напором и будем считать внутри бугра справедливым гидростатический закон давления

Рис. 12.1: Схема процесса расплывания бугра подземных вод

При этом оказывается, что пьезометрический напор постоянен по высоте бугра, то есть не зависит от координаты z:

H(r, z) = p(r, z) + pgz = pg(h(r)-z) + pgz = pgh(r) = f (r)

(Жидкость предполагается несжимаемой: .)

Следовательно, и закон Дарси в данном случае приобретает вид

где - скорость фильтрации, k - проницаемость пласта, - вязкость воды, и - единичные направляющие вектора вдоль осей r и z. В дальнейшем, учитывая направление вектора скорости , множитель для сокращения записи будем опускать. Соответствующий поток через цилиндрическую поверхность

(12.1)

Используя последнее выражение, несложно получить уравнение для высоты бугра h(r), поскольку изменение объема воды в выделенном цилиндрическом элементе происходит именно за счет баланса пересекающих его поверхность потоков.

Пусть вначале среда, пористость которой m, ненасыщена, то есть не содержит воды. В этом случае при внедрении воды в выделенный объем пласта его насыщенность будет возрастать от 0 до некоторого максимально возможного значения (ограниченного объемом защемленного воздуха). При уходе воды из рассматриваемого объема, за счет действия капиллярных сил, которые удерживают часть воды в порах и капиллярных каналах, водонасыщенность падает не до нуля, а только до некоторого конечного значения .

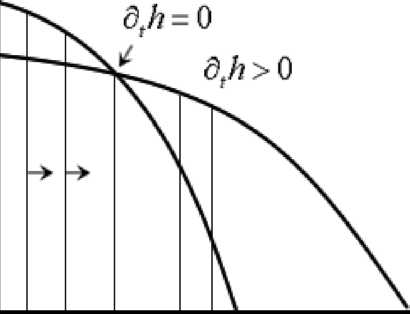
Тогда изменение количества воды в элементе объема между r и r + dr, обусловленное потоком q, определяется падением водонасыщенности от до в зоне, где происходит вытекание ( ) (рис.12.2). Параметр r₀ = r₀(t) - граница указанных областей: в области r < r₀ вода уходит из части пор, а в области r > r₀ входит в часть пор. Очевидно, это есть точка изменения знака производной , так как с одной стороны от нее высота бугра все время падает, а с другой - растет. Следовательно, непосредственно в этой точке (r₀) = 0. Координату границы бугра - точки, в которой водонасыщенность обращается в ноль, - обозначим r₁ (t) (рис. 12.1).

Будем для простоты считать, что и постоянны. Записывая балансовое соотношение

>

Г

z

А

d_th < О

т г +■ dr п

Рис. 12.2: Схема к выводу уравнения для h(r)

с учетом соотношения (12.1) для выделенных элементарных объемов (рис. 12.2) по обе стороны границы r₀, после несложных преобразований получаем результирующее уравнение для h(r)

.

Из физики процесса ясно, что решение h и расход Q~ = должны непрерывно зависеть от r.

Начальные условия естественно представить следующим образом: при t = 0 полный объем воды V, водонасыщенность в бугре , начальный радиус бугра . Не уменьшая общности, начальное распределение h(r, 0) удобно записать в виде

где h₀(s) - безразмерная функция, удовлетворяющая условиям

Итак, на полубесконечном интервале ищется непрерывное решение уравнения (12.2) с начальным условием (12.3), при этом должно выполняться условие непрерывности производной .

2. Анализ размерностей

Величина h зависит от следующих определяющих параметров: , число которых n = 6.

Выберем удобную систему единиц измерения.

Отношение характерной, например, максимальной, высоты бугра к его радиусу h(0,t)/r₁(t) не является определяющим параметром задачи, следовательно размерности вертикальной [H] и горизонтальной [L] координат формально можно считать независимыми. Физический смысл этого утверждения состоит в том, что вертикальный и горизонтальный размеры бугра могут как угодно сильно различаться, поэтому, и единицы для их измерения должны иметь совершенно различные масштабы, никак между собой не связанные. Поэтому выбираем систему HLT.

Тогда [h] = H; [r] = [r ] = L; [t] = T; [Q] = HL²; , откуда следует, что число определяющих параметров с независимыми размерностями k=3. В качестве таковых (для дальнейшего перехода к безразмерным переменным) целесообразно выбрать текущее время t, а также константы, определяющие характер процесса - Q и . Таким образом n-k=3, следовательно

Нас интересуют большие времена ( ), когда влияние деталей начального контура бугра исчезает. При

(поскольку от t вообще не зависит)

П₁ = const₂ > 0, если так же как t, т.е. r ~ t^1/4, а

П2 ~ r*/

Воспользуемся схемой рассуждений, рекомендованной в главе 6.

3. Случай полной автомодельности

Итак, первый шаг: предположение о полной автомодельности по параметру П₂ - исключаем его из рассмотрения:

П = Ф(П₁, 0, П₃) = Ф₁(П₁, П₃)

=Ф₁ (П₁, П₃) = Ф1

Здесь для удобства введены обозначения:

Тогда

Для координаты границы зон r₀, где = 0, имеем

причем

а для координаты границ бугра , где h обращается в нуль,

Подставляя (12.4) в уравнение (12.2), получаем для Ф₁ обыкновенное дифференциальное уравнение с разрывными коэффициентами. (Ниже вывод этого уравнения максимально подробно представлен для области .)

откуда окончательно имеем

Учитывая определение величины , и проведя элементарные преобразования, получаем уравнение

которое после сокращения на общий множитель приобретает вид

при

156

Совершенно аналогично в зоне получаем

при

Таким образом, обыкновенное дифференциальное уравнение имеет вид

откуда, с учетом того, что

получаем уравнение в полных дифференциалах

Первый интеграл его (с точностью до константы) очевиден:

Определим константы интегрирования. При (на оси симметрии) Ф₁ конечна (поскольку высота бугра h конечна везде), а в силу симметрии картины, следовательно, . За границей бугра , которой в безразмерных переменных соответствует координата , его высота h=0, следовательно, и сама безразмерная высота =0 и безразмерный поток . Отсюда . Таким образом, окончательный вид первого интеграла уравнения (12.5) есть

157

Легко видеть, что в частном случае , то есть при нулевой остаточной водонасыщенности ( = 0), что на практике реализуется чрезвычайно редко, предположение о полной автомодельности по параметру оказывается оправданным. Уравнение (12.6) при этом упрощается - исчезает разрывность коэффициента при старшей производной

или

В точках и уравнение (12.7) удовлетворяется автоматически (при функция Ф₁ = 0). В области произведение , поэтому уравнение (12.7) упрощается

откуда

При Ф₁ = 0, следовательно,

то есть

Для определения величины воспользуемся начальным условием (12.3) (точнее – условием, налагаемым на входящую в него безразмерную функцию ), представив его в виде

Подставляя в него в качестве выражение (12.8) получаем

Окончательный результат

представляет собой аналитическую функцию (рис. 12.3), удовлетворяющую уравнению (13.7) (а следовательно, при указанном условии – и уравнению (12.6)) и не содержащую переменную , то есть действительно является автомодельным решением I рода исходной задачи, так как для его получения оказывается достаточно одного анализа размерностей.

Рис. 12.3: График функции (??) - автомодельного решения задачи

Однако, в общем (и более реальном) случае и . При этом разрыв коэффициента при старшей производной уравнения (12.6) имеет место, что оказывает существенное влияние на решение.

Рассмотрим поведение функции Ф1 в точке , которая формально является обычной точкой из интервала (рис. 12.3). В этой точке уравнение (12.6) (после деления второй части уравнения на ) примет вид системы уравнений

Вычитая из первого уравнения системы (12.10) второе, получаем

откуда следует, что, так как и , , что заведомо неверно (рис. 12.3). Таким образом, предположение о полной автомодельности по параметру П₂ в общем случае не подтверждается, и приходится от него отказаться.

4. Случай неполной автомодельности

Тогда переходим к следующему этапу. Второй шаг: предположение о неполной автомодельности. Причем вспомним, что в общем случае при к нулю стремятся оба параметра - и . Не будем более искусственно уходить в область больших r, когда так, что бы П₁ оставался существенной величиной при . Тогда для произвольного r при , . Поэтому на втором шаге учтем неполную автомодельность «во всем ее объеме», то есть по обоим параметрам и . Тогда, в соответствии с установленным ранее алгоритмом (глава 6), при

Опуская тривиальные промежуточные выкладки (расписывание h в размерном виде и очевидные преобразования в комбинации ), получаем

(12.11)

где введены обозначения

Подстановка (12.11) в (12.2) (выкладки опущены) дает для Ф₂ уравнение

(12.12)

Но, поскольку явной зависимости Ф₂ от t быть не может – она зависит только от безразмерных переменных , - показатель степени t должен равняться нулю, откуда

(12.13)

Используя введенные в (12.11) обозначения и полученную связь (12.13) между и , можно показать, что

Соответственно, уравнение (12.12) примет вид

Выпишем граничные условия, накладываемые на решение этого уравнения. Во-первых, - из соображения симметрии – на оси симметрии . Во-вторых – на границе бугра

Поэтому, если в общем случае , в граничной точке с учетом (12.15) получаем связь . Используя ее, а также вновь (12.15), из (12.14) имеем

т.к.

(12.15)

На самом деле последняя запись для не совсем корректна - если сама Ф₂ и поток в точке непрерывны, то имеет в этой точке разрыв первого рода. Поэтому строгая запись должна иметь вид

Но, поскольку нас прежде всего интересует поведение решения внутри бугра, то есть в полуинтервале , будем рассматривать поведение функции при подходе к точке “изнутри” бугра, со стороны -0. Константу B удобно выбрать таким образом, чтобы радиус границы бугра =1.

Итак, окончательно имеем три граничных условия

При произвольном существует решения уравнения второго порядка, удовлетворяющего трем граничным условиям.

Но существуют собственные значения параметра , при которых это происходит, — следовательно показатель степени в законе движения границы бугра r₁ = определяется не из анализа размерностей, а из решения задачи (12.14),(12.16) на собственные значения.

162

^А Нл(М/ К \

—>

111 (ч /г.)

Рис. 12.4: Графическое представление численного решения задачи (??), (??)

Эта задача, аналогично рассмотренной в главе 5, решается численно. Из асимптотики (рис. 12.4), получаемой при больших временах (для фиксированного ), устанавливаем закон убывания максимальной высоты бугра (на оси )

или

где , а начальная высота h(0,0)=h₀. Отношение определяется из графика на рис. 12.4. Учитывая связь (13.13) между и определяем далее значение каждого из показателей, что дает временные законы падения максимальной высоты бугра

и распространения границы бугра

Решая серию задач с различными значениями каждый раз из графика, аналогичного представленному на рис. 12.4, соответствующее значение , получаем зависимость (рис. 12.5). Сами кривые имеют при этом вид, приведенный на рис. 12.6. Если теперь вспомнить, что представляет собой введенная в (12.11) константа

(12.17)

то приходим к следующему выводу.

1. Из графика, приведенного на рис. 12.5, видно, что при (остаточная водонасыщенность равна 0), когда . Тогда зависимость от r* в инварианте (12.17) пропадает, и имеет место полная автомодельность предельного режима, который соответствует сосредоточенному мгновенному источнику r*=0. При этом имеем

Рис. 12.5: График зависимости полученный в результате проведения серии

численных расчетов задачи

Рис. 12.6: Графический вид функции Ф₂

О ¹ /

^А Ф₂(/>

тривиальный инвариант

Q = const

1. Для и . В этом случае имеет место неполная автомодельность — при вследствие (12.17) возникает инвариант

и для сохранения неизменного предельного режима при уменьшении необходимо увеличивать Q в соответствии с этим инвариантом.