2.2. Расчёт с торсионами

На рисунке 4 приведена схема рамы с торсионами. Материал рамы – кремний поликристаллический. Масса рамы определяется как:

,

где l_k - длина контура рамы,

d - ширина контура рамы,

h₀ - толщина рамы,

ρ_Si - плотность кремния.

Расчёт длины торсиона рамы проводим из условия поворота рамы на градусов вокруг оси торсиона. Допускаемое напряжение в торсионе

,

Для материала торсиона имеем = 150 МПа. Сечение торсиона принимаем равным C₂∙h₀ (см. табл. 3).

Для соотношения коэффициенты и определяются по таблице 2. Отсюда:

.

Крутящий момент на торсионе рамы, соответствующий допускаемым напряжениям равен:

(8)

При заданном угле закручивания длина торсиона рамы определится из уравнения:

Расчёт коэффициента допускаемой динамической перегрузки рамы проводим из анализа напряжённого состояния при изгибе от действия весовой нагрузки, включающей массу зеркального элемента m₃ и массу рамы m_p.

Максимальные растягивающие напряжения в торсионе рамы равны

(9)

где

Коэффициент допустимой динамической нагрузки равен

(10)

2.3. Расчёт деформации зеркального элемента в рабочем диапазоне температур.

Надёжность работы двухкоординатного микрозеркала определяется температурной деформацией зеркального элемента, представляющего собой двухслойную пластинку Si – Me. В такой структуре материалы слоёв имеют большую разницу в коэффициентах термического расширения (в 3 – 5 раз). Величины коэффициентов для Si металлических отражающих слоёв приведены в таблице. Схема плоской деформации зеркального элемента показана на рисунке 5.

Для оценки влияния температуры на деформацию двухслойного элемента воспользуемся решением, изложенным в |3,6|. Считаем напряжённое состояние плоским, двухслойная пластина единичной ширины со свободными краями.

Прогиб и угол поворота сечения двухслойной пластины определим интегрированием уравнения (6)

(11)

,

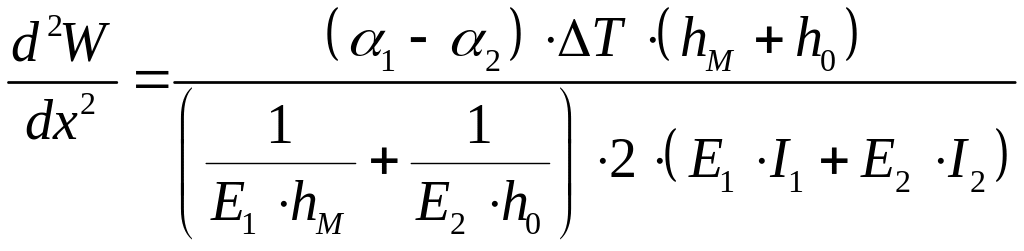где – изменение температуры от нормальной,

, – модули упругости металлического слоя и кремния.

, – моменты инерции сечений слоёв,

, – толщины металлического слоя и слоя кремния,

, – коэффициенты термического расширения металла и кремния.

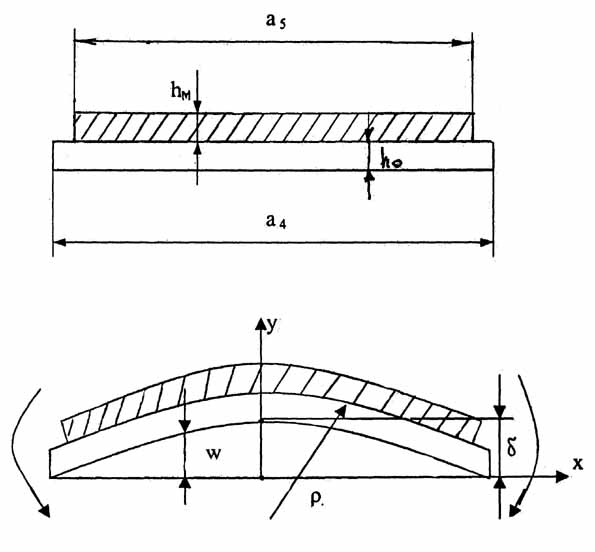
Рис.5 Схема температурной деформации зеркального двухслойного элемента.

При интегрировании уравнения в качестве граничного условия принимаем прогиб на границе пластины равный 0, угол поворота в центре в центре пластины равный 0 (см. рис.5).

Расчётное уравнение для определения угла поворота на периферии пластины имеет вид:

(12)

,

Уравнение для расчёта прогиба запишется так:

(13)

,

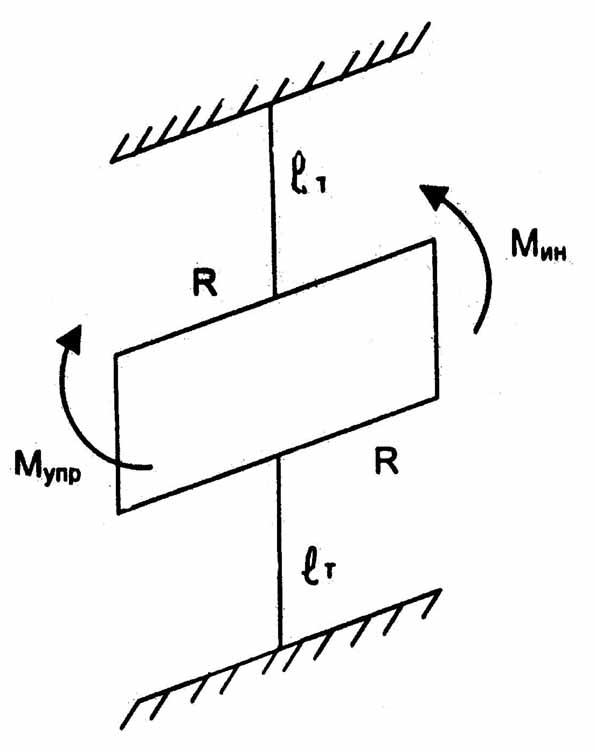
Рис.6 Схема колебания зеркального элемента относительно торсионов (относительно оси х)

2.4. Расчёт резонансной частоты зеркального элемента и микрозеркала.

Свободные колебания зеркального и микрозеркала (демприрование равно нулю) определяется действием инерционного и упругого моментов. Условие равновесия элемента запишется в виде:

или

(14)

где , – момент инерции твёрдого тела, - угол закручивания.

Решение уравнения (14) имеет вид |7|:

(15)

Собственная круговая частота, как следует из (15) определится зависимостью:

откуда циклическая частота будет равна:

(16)

где – момент, необходимый для закручивания элемента с двумя торсионами на один радиан; ω – период колебания.

Расчётное уравнение для определения циклической частоты записывается в виде:

(17)

где – длина торсиона, – момент инерции при кручении, I_M – момент инерции твёрдого тела относительно оси вращения, – модуль сдвига кремния (G ~ 0,4 E).

Величина рассчитывается по приведённым выше формулам для торсиона зеркального элемента и рамы.

Момент инерции твёрдого тела I_M определяется массой тела и расстоянием от центра масс до оси вращения. По |8| определяется как:

(18)

где R – расстояние от центра массы до оси вращения.

Для квадрата с сечением h∙h момент инерции относительно главной оси, проходящей через центр масс равен:

(19)