Вопрос 78.

Парадокс Кондорсе́ — парадокс теории общественного выбора, впервые описан маркизом Кондорсе в 1785 г.

Он заключается в том, что при наличии более двух альтернатив и более двух избирателей коллективная ранжировка альтернатив может быть цикличной (не транзитивна), даже если ранжировки всех избирателей не являются цикличными (транзитивны). Таким образом, волеизъявления разных групп избирателей, каждая из которых представляет большинство, могут вступать в парадоксальное противоречие друг с другом.

Обобщён теоремой «о невозможности» Эрроу в 1951 г.

На практике идея о необходимости ранжирования кандидатов реализована в голосовании по методу Шульце.

Принцип Кондорсе.

Кондорсе определил правило, по которому сравнение выбираемых альтернатив (кандидатов) производится с учетом полной ординалисткой информации о предпочтениях избирателей.

Согласно принципу Кондорсе, для определения истинной воли большинства необходимо, чтобы каждый голосующий проранжировал всех кандидатов в порядке их предпочтения. После этого для каждой пары кандидатов определяется, сколько голосующих предпочитает одного кандидата другому - формируется полная матрица попарных предпочтений избирателей.

На базе этой матрицы, используя транзитивность отношения предпочтения, можно попытаться построить коллективную ранжировку кандидатов.

Парадокс Кондорсе.

Введём для краткости обозначение:   будет означать, что голосующий предпочитает кандидата A кандидату B, а кандидата B — кандидату С.

• 1 человек: 

• 1 человек: 

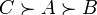
• 1 человек: 

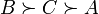
по итогам голосования двумя третями голосов получаем три утверждения:  ,  ,  . Но вместе эти утверждения противоречивы. В этом и состоит парадокс Кондорсе или парадокс коллективного выбора. Оказывается невозможным определить волю большинства и принять какое-то согласованное решение.

В силу симметрии в таком виде парадокс неразрешим никакими ухищрениями. Но если заменить отдельных избирателей в этом примере на три группы с близким, но не одинаковым числом избирателей, например, 9, 10 и 11, то метод Шульце позволяет формально определить победителя. Хотя парадоксальная цикличность коллективной ранжировки сохраняется.

Теорема Эрроу (также известна как «Парадокс Эрроу», англ. Arrow’s paradox) — теорема о невозможности «коллективного выбора». Сформулирована американским экономистомКеннетом Эрроу в 1951 году.

Смысл этой теоремы состоит в том, что в рамках ординалистского подхода не существует метода объединения индивидуальных предпочтений для трёх и более альтернатив, который удовлетворял бы некоторым вполне справедливым условиям и всегда давал бы логически непротиворечивый результат.

Ординалистский подход основывается на том, что предпочтения индивидуума относительно предлагаемых к выбору альтернатив не могут измеряться количественно, а только качественно, то есть одна альтернатива хуже или лучше другой.

В рамках кардиналистского подхода, предполагающего количественную измеримость предпочтений, теорема Эрроу в общем случае не работает.

Формулировка 1963 года

В формулировке 1963 года условия Эрроу таковы.

Универсальность

Отсутствие диктатора

Независимость от посторонних альтернатив

Эффективность по Парето, или принцип единогласия

если у каждого избирателя альтернатива x в списке стоит выше y, это же должно быть и в окончательном результате.

Для N≥2 и n≥3 не существует системы голосования, которая отвечает всем четырём условиям.

Доказательство теоремы Эрроу.

Введем следующие обозначения:

≻_i - предпочтения i-го агента; [≻^'] - профиль предпочтений (кортеж, элементами которого являются предпочтения всех агентов);

W : Lⁿ → L - функция общественного благосостояния; ≻_W - коллективные предпочтения.

Обозначим O - множество исходов, которые каждый агент ранжирует в соответствии со своими предпочтениями.

Дадим формальные определения:

Парето эффективность

W парето эффективна, если для любых исходов o₁, o₂ ∈ O, ∀i (o₁ ≻_i o₂) ⇒ (o₁ ≻_W o₂)

Независимость от посторонних альтернатив

W независима от посторонних альтернатив, если для любых исходов o₁, o₂ ∈ O и для любых двух профилей предпочтений [≻^'] и [≻^"] ∈ Lⁿ, ∀i (o₁ ≻_i^' o₂ ⇔ o₁ ≻_i^" o₂) ⇒ (o₁ ≻_W([≻^"_]) o₂ ⇔ o₁ ≻_W([≻^"_]) o₂)

Отсутствие диктатора

Считаем, что для W отсутствует диктатор, если не существует такого i, что ∀ o₁, o₂ ∈ O (o₁ ≻_i o₂ ⇒ o₁ ≻_W o₂ )

Теорема Эрроу

Если |O| ≥ 3, то любая Парето эффективная, независящая от посторонних альтернатив функция общественного благосостояния W имеет диктатора.

Доказательство проведем в 4 этапа.

Этап 1. Утверждение

Если каждый агент помещает исход b в самый верх или самый низ своего списка предпочтений, то и в ≻_W исход b тоже будет либо вверху, либо внизу списка.

Возьмем произвольный профиль [≻] такой, что в нем для всех агентов i исход b расположен либо вверху, либо внизу списка предпочтений ≻_i. Теперь допустим, что наше утверждение неверно, т.е. существуют такие a,c ∈ O, что a ≻_W b и b ≻_W c. Изменим тогда профиль [≻] так, чтобы для всех агентов выполнялось c ≻_i a, не изменяя при этом ранжирования остальных исходов. Обозначим полученный профиль [≻^']. Так как после такой модификации исход b для каждого агента все равно останется либо на самой верхней, либо на самой нижней позиции в списке его предпочтений, то из независимости W от посторонних альтернатив можно заключить, что и в новом профиле a ≻_W b и b ≻_W c. Следовательно, в силу транзитивности ≻_W получаем a ≻_W c. Но мы предположили, что для всех агентов c ≻_i a, тогда в силу парето эффективности должно быть c ≻_W a. Полученное противоречие доказывает утверждение.

Этап 2. Утверждение

Существует агент, который является центральным в том смысле, что, изменив свой голос, он может переместить исход b из самой нижней позиции в списке ≻_W в самую верхнюю позицию в этом списке.

Рассмотрим любой профиль предпочтений, в котором все агенты расположили исход b в самом низу своего списка предпочтений ≻_i. Ясно, что и в ≻_W исход b находится на самой нижней позиции. Пусть все агенты начали по очереди переставлять исход b с самой нижней на самую верхнюю позицию в своих списках предпочтений, не меняя при этом ранжирования остальных исходов. Пусть n^* - агент, который переставив таким образом b, изменил ≻_W. Обозначим [≻¹] - профиль предпочтений как раз до того, как n^* переместил b, а [≻²] - профиль предпочтений сразу же после того, как n^* переместил b. Таким образом, в [≻²] исход b изменил свою позицию в ≻_W, при этом для всех агентов b находится либо на самой верхней, либо на самой нижней позиции ≻_i. Следовательно, в силу утверждения, доказанного на Этапе 1, в ≻_W исход b занимает самую верхнюю позицию.

Этап 3. Утверждение

n^* - диктатор над всеми парами <a,c>, не включающими в себя b.

Выберем из пары <a,c> любой элемент. Без потери общности, выберем a. Далее из профиля [≻²] построим [≻³] следующим образом: в ≻^n* переместим исход a на первую позицию, оставив остальное ранжирование неизменным; произвольным образом для всех остальных агентов поменяем местами друг с другом a и c. Тогда, как и в [≻¹] получим, что a ≻_W b (в силу независимости от посторонних альтернатив) и, как и в [≻²] получим, что b ≻_W c. Тогда a ≻_W c. Теперь построим профиль предпочтений [≻⁴] следующим образом: для всех агентов поместим исход b на произвольную позицию в списке предпочтений ≻_i, для агента n^* поместим исход a в произвольную позицию до исхода с. Ясно, что в силу независимости от посторонних альтернатив a ≻_W c. Мы получили, что все агенты, кроме n^* имеют совершенно произвольные профили предпочтений, а результат a ≻_W c получился исходя только лишь из предположения, что a ≻_n^* c.

Этап 4. Утверждение

n^* - диктатор над всеми парами <a,b>.

Рассмотрим какой-нибудь исход с. В силу Этапа 2 существует некоторый центральный агент n^** для этого исхода, он же является диктатором для всех пар <A,B>, где, в частности, A = a, B = b. Но n^* и сам может менять ранжирование в ≻_W (это рассматривалось на Этапе 2). Следовательно, можно заключить, что n^** совпадает с n^*. Доказательство завершено.