20.5. Функции

Функция  это подпрограмма, в результате выполнения которой происходит вычисление значения скалярного или строкового типа.

Заголовок функции имеет вид

В разделе операторов описания функции должен быть хотя бы один оператор присваивания:

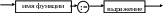
Значение последнего выражения, присвоенного имени функции, будет возвращено в точку вызова функции. Но использовать имя функции в качестве переменной, которой присвоено значение, недопустимо.

20.6. Обращение к функциям (вызов функций)

Синтаксически вызов функции не отличается от вызова процедуры:

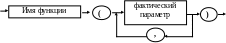
Но вызов функции не является оператором. Обратиться к функции можно всюду, где допустимо использование значения типа, возвращаемого функцией. Обращение к функции может быть операндом в выражении, фактическим параметром-значением.

Пример 3. Программа для проверки, упорядочена ли по невозрастанию данная целочисленная последовательность длиной не больше 100:

Program sort_check;

const MaxLen=100;

type t_range =1.. MaxLen;

t_vect= array[t_range] of integer;

function is_sort(a : t_vect; n : t_range): boolean;

{Логическая функция проверяет, упорядочена ли по невозрастанию последовательность a длины n}

var i : t_ range;

begin i:=2;

while (i<=n) and (a[i-1]>=a[i]) do

i := i+1;

is_sort := i>n

end;

var i, n : t_range; a : t_vect;

begin write(‘Введите длину последовательности’, MaxLen); read(n);

writeln(‘Введите члены последовательности’);

for i := 1 to n do

read(a[i]);

if is_sort(n, a) then writeln(‘ Последовательность упорядочена’)

else writeln(‘ Последовательность неупорядочена’)

end.

20.7. Побочный эффект функций

Основное назначение функции  возвращение значения в точку вызова, но функция так же, как и процедура, может изменять значения своих параметров-переменных. Такие функции называются функциями с побочным эффектом.

Пример 4. Описание логической функции поиска элемента, равного x, в целочисленном массиве а длиной n100. В качестве побочного эффекта параметру i присваивается номер первого из элементов, равных х. Используем типы, описанные в примере 3:

function el_search(a: t_vect; n: t_range; x: integer; var i: t_range): boolean;

begin i:=1;

while (i<=n) and (x<>a[i]) do

i := i+1;

el_search:= i<=n

end;

20.8. Рекурсивные подпрограммы

В математике рекурсией называется способ описания функций или процессов через самих себя. Например,

В некоторых языках программирования, в том числе и в Паскале, допустимо, чтобы подпрограмма вызывала себя. Такие подпрограммы называются рекурсивными.

Рекурсивная подпрограмма обязательно удовлетворяет двум требованиям:

1. имеет нерекурсивный выход;

2. при каждом рекурсивном обращении задача упрощается, приближаясь к нерекурсивному решению.

При решении некоторых задач можно использовать как рекурсивный, так и итеративный алгоритм. Преимущество рекурсивных подпрограмм заключается в простоте написания, легкости понимания. Обычно это касается задач, связанных с процессами, рекурсивными по своей природе. Но рекурсивные алгоритмы, как правило, менее эффективны из-за затрат времени на организацию стека. При каждом обращении в стеке запоминаются значения всех локальных переменных, параметров и коды возврата. Глубина рекурсии (количество обращений к себе) ограничена объемом памяти стека. При глубокой вложенности рекурсии может произойти переполнение стека.

Пример 5. Опишем рекурсивную и итеративную функцию для вычисления n! :