Контрольная работа 6

Задача 1. При производстве двух видов товаров (А и В) предприятие использует три типа ресурсов (I, II и III). Для производства единицы товара А требуется , и единиц ресурсов I, II и III соответственно. Для производства единицы товара В требуется , и единиц ресурсов I, II и III соответственно. Предприятие располагает фондами ресурсов I, II и III в количествах , и соответственно. Прибыль от реализации единицы товара А составляет рублей, а от реализации товара В – рублей.

Найти оптимальный план производства и его максимальную прибыль симплексным и геометрическим методами.

Данные задачи (по двум последним цифрам шифра студента … a b):

, , , ,

, , , ,

, , .

Задача 2. Решить методом искусственного базиса задачу оптимизации (данные по последним цифрам шифра студента … a b):

Задача 3. На трех предприятиях , и производится однородный продукт в количестве , и соответственно. Этот продукт следует доставить пяти потребителям , , , и , заказы которых равны соответственно , , , и . Матрица стоимости перевозок единицы товара

.

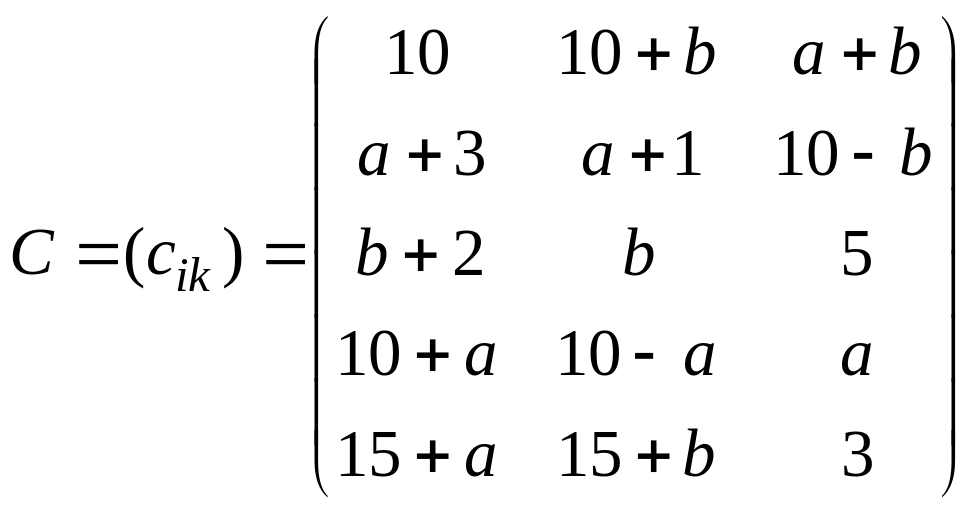Величины , , , , , , , записаны по последним цифрам шифра студента … a b. Найти методом потенциалов оптимальный план перевозок.

6. Линейное программирование. Основные понятия и экономическая интерпретация

Математическое программирование занимается построением алгоритмов или программ конструктивного решения задач оптимизации, т.е. задач на наибольшее или наименьшее значения функции нескольких переменных при заданных ограничениях. В общем виде такие задачи можно описать следующим образом:

,

т.е. максимизировать функцию при условии

или ;

,

т.е. минимизировать функцию при условии

или .

Оптимизируемая функция называется целевой, а область ограничений (или допустимое множество) является областью в многомерном евклидовом пространстве , векторы которого или имеют декартовых координат, а скалярное произведение определяется как , что аналогично обычному скалярному произведению в пространстве . В евклидовом пространстве , как и в трехмерном пространстве, определяются такие понятия, как базис, разложение по базису, свойство ортогональности и т.п. Так как аналитически области в задаются системами неравенств или равенств, то условие означает, что

,

где – некоторые заданные функции. При этом в ограничениях можно рассматривать только неравенства, так как равенство есть частный случай неравенств вида . Отметим что, если все неравенства нестрогие , тогда область будет замкнутой, т.е. содержащей все точки своей границы.

Если область ограничений непустая Ǿ), ограничена и замкнута, а целевая функция непрерывна, то по теореме Вейерштрасса задача оптимизации всегда имеет решение, т.е. существуют такие точки , для которых и . От­метим, что таких оптимальных точек может быть несколько (аль­тернативные решения), но оптимальное значение всегда одно.

При нарушении условий теоремы Вейерштрасса решение задачи оптимизации может не существовать.