Уравнение теплопередачи

Для протекания процесса передачи тепла необходимо нали­чие некоторой разности температур между горячим и холодным теплоносителями. Эта разность температур является движущей силой процесса теплопередачи и называется температурным на­пором. Если Т — температура горячего теплоносителя, a t — тем­пература холодного теплоносителя, то температурный напор

Δ t = T - t

Чем больше температурный напор, тем выше скорость пере­дачи тепла, причем количество тепла, передаваемого от горячего теплоносителя к холодному (т. е. тепловая нагрузка аппарата), пропорционально поверхности теплообмена F, температурному напору Δ t и времени τ:

Q = kF Δ t τ

Здесь k — коэффициент пропорциональности, называемый коэффициентом теплопередачи и представляющий собой количе­ство тепла, передаваемое через единицу поверхности в единицу времени при температурнбм напоре, равном единице. Если Q выражено в дж, F в м², τ в сек и Δ t в град, то коэффициент теп­лопередачи имеет размерность

k = Дж/м² сек град =Вт/ м² град

k = f(l,d,c,ρ,μ….)

Он ориентировочно принимается по справочным данным или рассчитывается по сложным зависимостям.

При непрерывных процессах под тепловой нагрузкой Q по­нимают количество тепла, передаваемое за единицу времени (вт); тогда уравнение (11-8) можно написать в виде:

Q = kF Δ t

Уравнение теплопроводности

Если тепло переносится путем теплопроводности через стен­ку, то, согласно закону Фурье, количество передаваемого тепла пропорционально поверхности F, разности температур между обеими поверхностями стенки Δt_ст = t_ст1- t_ст2 времени τ и об­ратно пропорционально толщине стенки δ:

Q = λ F Δ t_ст τ/ δ

где t_ст1и t_ст2 —температуры поверхностей стенки.

Коэффициент пропорциональности λ называется коэффици­ентом теплопроводности (или просто теплопроводностью) и имеет размерность

λ = Дж м/м² сек град =Вт/ м град

Коэффициент теплопроводности представляет собой количе­ство тепла, проходящее в единицу времени через единицу по­верхности при разности температур 1°С на единицу толщины стенки. Этот коэффициент зависит от свойств материала стенки и от ее температуры.

Для непрерывного процесса уравнение можно представить в виде:

Передача тепла через стенку

Плоская стенка

Рассмотрим сложный процесс передачи тепла через плоскую стенку от горячего теплоносителя к холодному. Характер изме­нения температур показан на рис. 1 В слое горячего тепло­носителя температура изменяется от t₁ до t_ст1 по толщине стенки от t_ст1 до t_ст2 и в слое холод­ного теплоносителя от t_ст2 до t₂

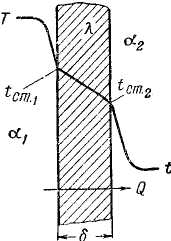
Напишем уравнения передачи теп­ла конвекцией от горячего теплоноси­теля к стенке, путем теплопроводно­сти через стенку и конвекцией от стен­ки к холодному теплоносителю:

— коэффициенты теплоот­дачи от горячего тепло­носителя к стенке и от стенки к холодному теп­лоносителю.

Поверхность теплообмена F равна поверхности стенки и при плоской стенке является постоянной величиной.

При установившемся процессе количества тепла, передавае­мые от горячего теплоносителя к стенке (Q₁), через стенку (Q_CT.) и от стенки к холодному теплоносителю (Q₂), должны быть равны между собой, т. е.

Q₁ = Q_CT. = Q₂ = Q

Тогда:

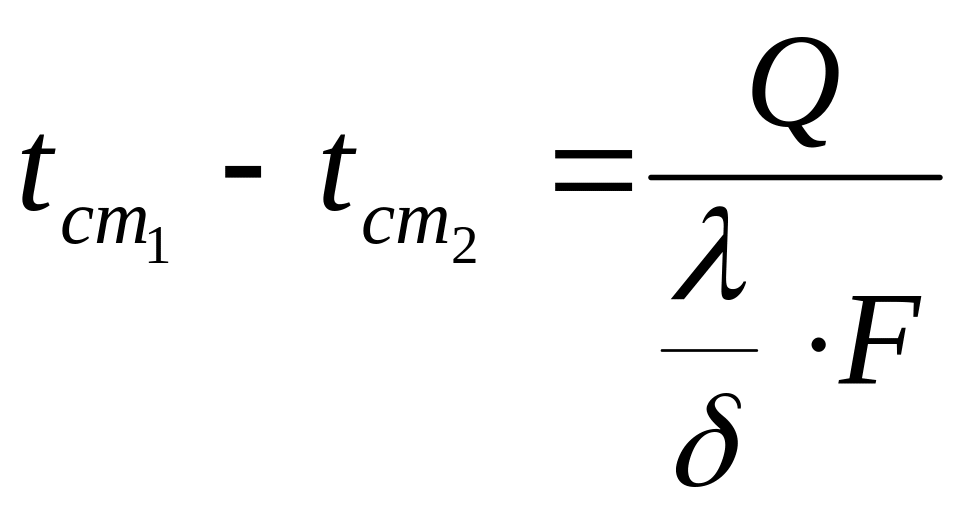
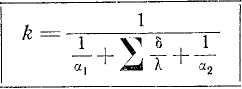
- коэффициент теплопередачи (Вт/м² град)

α₁ и α₂ – коэффициенты теплоотдачи при конвективных процессах

тепловое сопротивление

Если стенка состоит из нескольких слоев толщиной δ₁, δ₂ δ₃ с теплопроводностями λ₁, λ₂, λ₃ то тепловые сопротивления будут равны δ₁/ λ₁

δ₂/ λ₂ и δ₃/ λ₃, а тепловые сопротивления всей стенки составит