Движение жидкости по трубопроводам

Р₁ = Р₂ +ΔР

где ΔР – потери давления на трение.

ΔР =

Где –λ – коэффициент гидродинамического трения.

λ = f (Re, ε),

где ε – относительная шероховатость стенок трубопроводов.

Для ламинарного потока λ зависит только от величины Re и определяется по формуле

λ = 64/Re

Для турбулентного потока λ можно определяется по сложным зависимостям, либо по уже рассчитанным графикам.

Местные сопротивления

1. Потери давления, обусловленные изменением направления потока

Резкий поворот (90 ) Плавный поворот

2. Потери давления, связанные с изменением сечения

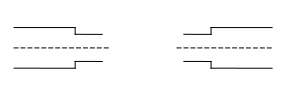
Внезапное сужение Внезапное расширение

3. Потери давления, обусловленные изменением направления и скорости

а) запарные (регулировочные) приспособления: задвижка, вентиль

б) Приборы КИП: термометр, диафрагма

Таким образом, потери давления на движение по трубопроводам с учетом местных сопротивлений можно выразить так:

ΔР =

Разделение жидких неоднородных систем

Под неоднородной системой понимают систему, состоящую из различных фаз, например жидкости и твердых частиц, жидкости и газа и т. д. Любая неоднородная система состоит из двух и более фаз. Одна фаза, дисперсная, или внутренняя, находится в мелкодисперсном состоянии; другая фаза, дисперсионная, или внешняя, является сплошной, окружает отдельные частицы дис­персной фазы и представляет собой среду, в которой распре­делены частицы дисперсной фазы.

В зависимости от физического состояния фаз различают сле­дующие неоднородные жидкие и газообразные системы:

Неоднородные Дисперсионная Дисперсная

системы (сплошная) фаза фаза

Суспензия Жидкость Твердое вещество

Эмульсия Жидкость Жидкость

Пена Жидкость Газ

Пыль, дым Газ Твердое вещество

Туман ....... Газ Жидкость

Всякая неоднородная система характеризуется концентраци­ей дисперсной фазы и размерами ее частиц.

Все системы, состоящие из жидкой и твердой фаз, в зависи­мости от размеров частиц твердого вещества могут быть условно разделены на четыре группы:

Системы Размер твердых

частиц, мк

Грубые суспензии ... > 100

Тонкие суспензии . . . 0,5—100

Мути . 0,1—0,5

Коллоидные растворы . < 0,1

Можно считать, что граница между суспензиями (взвесями) и коллоидными растворами определяется появлением броунов­ского движения твердых частиц. С возникновением броуновского движения эти частицы не могут осаждаться под действием силы тяжести.

Материальный баланс разделения

Рассмотрим материальный баланс разделения суспензий, как наиболее распространенного процесса разделения жидких неод­нородных систем.

Пусть G_с — количество разделяемой суспензии (в кг), х₁ — весовая доля твердой фазы в суспензии. В результате разделе­ния получается осадок в количестве G_ос. кг с содержанием твер­дой фазы х₂ и влажностью w = 1 — х₂ и жидкость, количество которой равно G_ж кг.

Тогда уравнения материального баланса будут иметь сле­дующий вид:

для всей системы

G_с = G_0С + G_ж (8-6)

для твердой фазы

G_сх₁ = G_0С х₂ (8-7)

или

G_сх_г =G_0С (1 — w) (8-8)

Совместным решением уравнений (8-6) и (8-8) определяют количество влажного осадка и количество жидкой фазы.

Скорость осаждения

Независимо от режима движения и формы твердого тела, движущегося в жидкости, сила сопротивления R среды (в н) может быть выражена в общем виде законом Ньютона:

R =

где — коэффициент сопротивления среды;

Р—площадь проекции тела на плоскость, перпендикуляр­ную к направлению его движения, м²;

р — плотность среды, кг/м³;

т — скорость, м/сек.

В случае движения шарообразных частиц закон сопротивле­ния Ньютона выражается равенством:

где — диаметр частицы.

В выражении (6-90) можно принять за коэффициент сопро­тивления среды величину . Тогда закон сonротивления примет следующий вид:

(6-91)

откуда

Величина представляет собой критерий Еu и в соответствии с общей зависимостью (6-47) является функцией критерия Rе, который в данном случае рассчитывается по диаметру d частицы.

При движении шарообразных частиц зависимость коэффициента сопро­тивления от критерия Рейнольдса Rе может быть представлена следующим

Характер движения

Ламинарный (уравнение Стокса)

Промежуточный (уравнение Аллена)

Турбулентный (уравнение Нью­тона)

Коэффициент сопротивления R для частиц нешарообразной формы боль­ше, чем для шарообразных, и зависит от критерия Rе и коэффициента формы (сферичности) Ф, который представляет собой отношение поверхности шара /шар.» имеющего такой же объем, что и частица неправильной формы, к дей­ствительной поверхности ^_ч частицы:

(6-93)

Ниже приведены значения коэффициента Ф для частиц различной формы:

Форма частиц . . . Шар Куб Цилиндр Диск

Коэффициент Ф . . 1 0,806 0,69 0,32

* h —высота цилиндра (диска); r —радиус основания.

Рассмотрим общий закон сопротивления на примере движе­ния твердой частицы в неподвижной среде. Пусть на частицу массой т действует некоторая сила Р (рис. 6'-22). В противоположную сторону действует сила сопро­тивления среды Я. Поэтому уравнение движения частицы имеет следующий вид:

Р — Р = та

где а — ускорение, с которым движется частица.

В исходный момент, когда скорость частицы w = 0, сопротивление среды R = 0. Однако как только частица начинает двигаться, по мере нарастания ее скорости увеличивается сила сопротивления cреды и уменьшается ускорение а частицы. Через короткий промежуток времени сила сопротивления возрастает до величины R = Р. За этот же период ускорение уменьшается от начальной величины до а = 0. В момент, когда силы, действующие на частицу, уравновешиваются, ускорение становится равным нулю, ско­рость w частицы — постоянной, а движение ее — равномерным. Эта постоянная скорость называется скоростью осаждения и обозначается через w₀.

Время, в течение которого частица достигает постоянной ско­рости, теоретически равно бесконечности, так как возрастание скорости при падении частицы все время замедляется; однако практически скорость приближается к постоянной уже через ни­чтожно малый промежуток времени (сотые доли секунды) после начала падения.

Чтобы происходило осаждение твердых частиц, т. е. выделе­ние их из жидкости или газа, действующая сила (сила тяжести,

центробежная сила и др.) должна быть равна или больше силы сопротивления среды:

Р>Н

Скорость осаждения может быть определена из уравнения (6-91). Заменив в этом уравнении Р на Р, найдем значения ско­рости

Коэффициент сопротивления ф зависит от критерия Ре, в кото­рый входит искомая скорость осаждения ту₀ (Ре = -^—-). По­этому уравнение (6-94) решается только подбором; принимая произвольно величину Не, определяют ф и находят по формуле (6-94) величину йу₀, после чего рассчитывают действительное значение Не. Расчет повторяют до совпадения расчетной вели­чины Не с предварительно принятой.

Расчет упрощается, если исключить искомую скорость w₀ из выражения (6-91), умножив обе его части на . Тогда, заменяя

R на Р, получим;

При падении частицы диаметром й под действием силы тя­жести сила Р равна весу частицы в жидкости:

P

где g— ускорение силы тяжести, м/сек².

и — плотность частицы и среды, кг/м³.

Таким образом

где Аг — критерий Архимеда (см. стр. 149).

Подставляя в это выражение значения ф по уравнениям Стокса, Аллена или Ньютона (стр. 172) и решая полученные урав­нения относительно Rе, найдем:

при Ре < 2 или Аг < 36 Ре = 0,056 Аг (6-95)

при Rе = 2 --500 или Аг = 36--83 • 10³ Rе = 0,152 Аг⁰'⁷¹⁵ (6-96) при Rе > 500 или Аг > 83 • 10³ Rе = 1,74 Аг^0,5 (6-97)

Определив критерий Rе по одной из приведенных формул (в зависимости от величины Аг), легко найти скорость осаждения: (6-98)

В этой формуле w₀ является скоростью осаждения единичной частицы, при движении ее независимо от других частиц, в не­ограниченном объеме (скорость свободного осаждения). Расчет чю₀ при одновременном осаждении многих частиц приведен на стр. 244.

Скорость осаждения нешарообразных частиц меньше, чем шарообразных, и ее обычно определяют экспериментальным пу­тем.

Если принять скорость осаждения шарообразных частиц с гладкой поверхностью за w₀, то для частиц другой (нешарооб­разной) формы скорость осаждения приближенно можно счи­тать равной 0,75 w

При движении жидких капель в газе или жидкости, а также пузырьков газа в жидкости уравнения для хю₀ усложняются вследствие изменения формы капель или пузырьков при их дви­жении.

Выше рассмотрен общий закон движения тел в жидкости и определена скорость свободного осаждения твердых частиц. С увеличением концентрации твердой фазы сус­пензии сопротивление среды движению осаждающихся частиц начинает зависеть не только от размера и формы частиц, но и от концентрации твердой фазы в суспензии. Осаждение в огра­ниченном объеме при большой концентрации твердой фазы, ко­гда соседние твердые частицы при движении соприкасаются друг с другом, называется стесненным осаждением. При стес­ненном осаждении сопротивление движению твердых частиц складывается из сопротивления среды и сопротивления, обус­ловленного трением и ударами твердых частиц друг о друга. Вследствие этого скорость стесненного осаждения всегда меньше скорости свободного осаждения тех же частиц.

Объемная доля жидкости в суспензии составляет

где —объем жидкости в суспензии;

— объем твердых частиц в суспензии.

В концентрированных суспензиях жидкость движется по из­вилистым каналам между твердыми частицами и сопротивление среды является функцией е, которую обозначим Ф(е). Вместе с тем движение твердых частиц под действием сил тяжести (при отстаивании) является в большинстве случаев ламинарным. По­этому, подставив в общую формулу (6-91) сопротивления среды значение коэффициента ф = -=— — —~ (стр. 172), полу­чим частное выражение сопротивления среды Я для ламинарной области, или так называемый закон Стокса:

Н = Зтт йут Соответственно сопротивление среды в условиях стесненного осаждения может быть выражено следующим образом:

^"■ — Ф(о'~ Ф(0 ⁽⁸"¹⁰⁾

При плотности твердой фазы р_тв. и плотности жидкой фа­зы р_ж плотность суспензии можно определить по формуле

Рс = ер_ж+(1— е)р_тв.

Разность плотностей Ар твердой фазы и суспензии будет равна:

^ДР = Ртв. — Рс = Ртв. — [^еРж + (1 — ^е) Ртв.] = (Ртв. — Рж) ^е

Подставляя значение Ар в выражение силы тяжести Р (стр. 174) и приравнивая Р сопротивлению среды /?, получим:

71Й³ , . _ ЗТС Й[АДО

~0~ 8 (Ртв. Рж) ^в ф (_Е)

Откуда после сокращений находим скорость жидкости отно­сительно твердых частиц. Она равна скорости движения твердых частиц относительно жидкости

_а, ₌ ^!С(Рт|-р_ж)_{еф(е) (8}._п)

Однако для расчета процесса отстаивания необходимо опре­делить скорость движения твердых частиц не относительно жид­кости, а относительно стенок аппарата (отстойника). При этом следует учесть, что объемные скорости обеих фаз при осаждении равны, так как объем твердых частиц, опускающихся вниз, вы­тесняет вверх равный объем жидкости.

Пусть слой суспензии в аппарате имеет площадь основания Р и высоту Н. Доля площади поперечного сечения слоя суспензии, доступная для прохода жидкости, равна Ре. Путь, пройденный в единицу времени вытесненной вверх жидкостью, или скорость подъема жидкости, составляет:

Ли»

Эта скорость равна искомой скорости осаждения о»₀ твердых частиц:

щ = гго

Подставляя в это выражение значение да из уравнения (8-11), получим окончательную формулу :

щ = ^а'^е(?^~^ы)гЩ(б)