2. 4. По передаточной функции замкнутой системы построим кривую переходного процесса (на эвм).

Передаточная функция замкнутой системы:

Построим для данной передаточной функции кривую переходного процесса по точкам, полученным из расчета на ЭВМ.

h(t)	0,24	0,3	1,21	2,82	5	6,84	7,7	10,99	13,3	14,7
t	0,001	0,001	0,021	0,068	0,106	0,124	0,129	0,137	0,140	0,140

Таблица экспериментальных данных.

Кривая переходного процесса замкнутой системы, построенная по экспериментальным данным, полученным на ЭВМ.

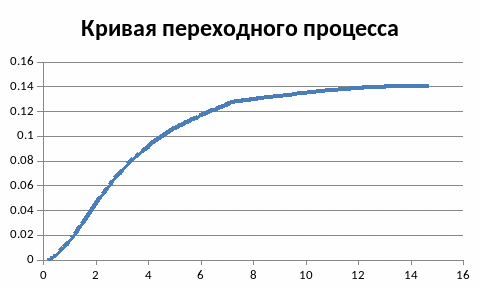
2. 4. 1. Определение основных показателей качества по кривой переходного процесса.

1. Максимальное перерегулирование – максимальное отклонение переходной характеристики от установившегося значения переходной величины, выраженное в относительных единицах.

2. Колебательность процесса:

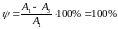
(определяется как отношение разности двух соседних амплитуд, направленных в одну сторону, к большей из них в относительных единицах)

3. Время регулирования – t_регул – минимальное время от начала нанесения возмущения до момента, когда регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью;

Определим по графику время регулирования t_регул = 11,2

Вывод.

Данная система автоматического регулирования отвечает требуемым показателям качества в динамике, т.к. величина максимального перерегулирования составляет 0% и колебательность процесса равна 100%. Однако, данная система в статике неработоспособна, т.к. имеет большую статическую ошибку равную 83%. Для того чтобы данная система была работоспособна в статике необходима уменьшить статическую ошибку. Для уменьшения статической ошибки необходима увеличить k_раз.. Но увеличение k_раз. ведёт к уменьшению запаса устойчивости, поэтому увеличивать k_раз. нужно очень осторожно.

Раздел №2 Синтез системы автоматического регулирования.

1. Последовательная коррекция

При последовательной коррекции корректирующее звено включают в прямую цепь регулирования. Схема последовательной коррекции имеет вид:

При выборе последовательного корректирующего звена необходимо помнить, что дифференцирующие звенья увеличивают запас устойчивости системы и увеличивают ее быстродействие, интегрирующие – улучшают статику системы, но уменьшают запас устойчивости системы, безинерционные – уменьшают статическую ошибку системы (и, если К>1 и уменьшают при этом запас устойчивости системы).

В данном случае, необходимо уменьшить статическую ошибку. При этом величина максимального перерегулирования не должна превысить 25%, колебательность должна быть больше 75%, а время регулирования не должно превышать 14-15с.

Заменим W_исх. (р) и W_посл. (р) на эквивалентную функцию W_ск. (р)

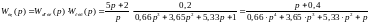
Рассмотрим влияние этого звена на статику системы:

;

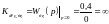Раасмотрим влияние выбранного последовательного звена на динамику с помощью АФЧХ скорректированной системы.

Построим для данной передаточной функции АФЧХ по точкам, полученным из расчета на ЭВМ.

Re	0	-0,09	-0,29	-0,46	-0,53	-0,6	-0,63
Im	0	-0,04	-0,51	-1,33	-1,88	-3,11	∞

Как видно из годографа Найквиста система имеет запас устойчивости по модулю равный 1 и запас устойчивости по фазе равный 70^о.

Теперь построим кривую переходного процесса (на ЭВМ)

h(t)	0,25	0,32	0,82	1,92	3,6	6,42	9,45	11	19,22	22,5
t	0,01	0,01	0,06	0,27	0,6	0,93	1,04	1,05	1,01	1,01

Таблица экспериментальных данных.

tрег

Определение основных показателей качества по кривой переходного процесса.

1) Время Регулирования

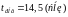
2) Величина максимального перерегулирования.

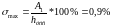
3) Колебательность процесса.

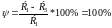
Вывод.

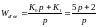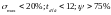Применяя последовательную коррекцию к данной системе автоматического регулирования, и взяв в качестве корректирующего звено, равное , удалось уменьшить статическую ошибку до 0% (улучшить статику, запас по фазе несколько уменьшился (до 70%). Время регулирования увеличилось на 3,3 с , т.е. ухудшилось быстродействие. Система также отвечает основным показателям качества в динамике ( ). Статическая ошибка уменьшена до 0, значит, данная система является астатической, следовательно система работоспособна в статике.

Выводы

В начале курсового проекта была получена система автоматического регулирования, которая удовлетворяла требуемым показателям качества в динамике, но была не работоспособной в статике. Для приведения системы в работоспособное состояние была предпринята последовательная. Последовательная коррекция улучшила поведение системы в статике (уменьшив статизм системы до 0%), и немного ухудшила динамику системы (уменьшив запас устойчивости по фазе).