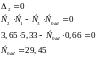Содержание

Y

Задание 2

I. Анализ системы автоматического регулирования. 2

II. Синтез системы автоматического регулирования. 3

РАЗДЕЛ №1 4

Анализ системы автоматического регулирования. 4

1. Структурные преобразования. 4

1.1. Приведение системы к одноконтурной, определение числовых значений параметров САР. 4

1.2. Передаточные функции разомкнутой и замкнутой систем. 5

1.3. Определение статизма системы. 6

2. Исследование замкнутой системы на устойчивость с применением критериев Гурвица, Михайлова и Найквиста. 6

2.1. Алгебраический критерий Гурвица. 6

2.2. Частотный критерий Михайлова. 7

2.3. Частотный критерий Найквиста. 9

2.4. По передаточной функции замкнутой системы построим кривую переходного процесса (на ЭВМ). 11

РАЗДЕЛ №2 14

Синтез системы автоматического регулирования. 14

1. Последовательная коррекция 14

Выводы 17

Список использованной литературы 18

Задание

1. Анализ системы автоматического регулирования.

Вариант:776

Исходные данные.

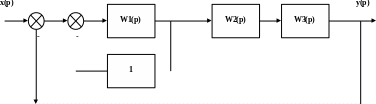
1. Структурная схема исследуемой САР

2. Передаточные функции звеньев САР (табл.1).

Таблица №1

W1(p)	W2(p)	W3(p)

3. Параметры звеньев (передаточные коэффициенты и постоянные времени) (табл.2).

Таблица №2

К1	К2	К3	Т1(с)	Т2(с)	Т2’(с)	1
1	0,2	3	3	5	2	3

Требуется:

1. Провести структурное преобразование САР, превратив систему в одноконтурную. При этом звенья САР, охваченные местными обратными связями, заменить эквивалентными звеньями и определить для них передаточные функции. Определить числовые значения параметров эквивалентных звеньев.

2. По передаточным функциям звеньев одноконтурных САР определить передаточные функции и характеристические уравнения разомкнутой и замкнутой систем.

3. Определить передаточный коэффициент системы и статизм системы.

4. Исследовать замкнутую систему на устойчивость при помощи критерия устойчивости Гурвица. Определить значение критического коэффициента усиления системы. Если замкнутая САР неустойчива, то изменив значение одного ( или обоих ) коэффициентов обратных связей ( β₁, β₂) или значение одного из коэффициентов усиления звеньев ( к₁, к₂, к₃) добиться ее устойчивости.

5. Скорректированную (исходную, если система устойчива) систему исследовать на устойчивость частотными критериями Михайлова и Найквиста. По критерию Михайлова найти значение критического коэффициента усиления системы, по критерию Найквиста определить запас устойчивости замкнутой САР по модулю и фазе.

6. На основании математического описания системы построить кривую переходного процесса замкнутой САР. Для расчета кривой переходного процесса на ЭВМ целесообразно воспользоваться программным средством «ТАУ».

7. По кривой переходного процесса определить основные показатели качества: время регулирования – t_рег, величину перерегулирования – σ_max, колебательность процесса – ψ, и сделать вывод, отвечает исследуемая САР требуемым показателям качества (σ_max ≤ 20%, ψ ≥ 75 ÷ 90%) или нет.

2. Синтез системы автоматического регулирования.

Исходные данные:

1. Структурная схема одноконтурной САР, полученная в разделе I.

2. Переходная характеристика исследованной замкнутой САР и показатели ее качества ( коэффициент статизма, время регулирования – t_рег, перерегулирование – σ_max и колебательность процесса – ψ).

Требуется:

1. Ввести в исследуемую систему последовательное корректирующее звено по схеме (рис.1.):

W_исх(P) – передаточная функция исходной разомкнутой системы;

W_посл(P) – передаточная функция вводимого корректирующего звена.

Рис.1. Схема последовательной коррекции

Введение корректирующего звена должно обеспечить статическую ошибку системы (коэффициент статизма ) ≤ 2 ÷ 5%, колебательность переходного процесса ψ ≥ 75 ÷ 90%, а время регулирования t_рег меньше 20с

РАЗДЕЛ №1

Анализ системы автоматического регулирования.

1. Структурные преобразования.

1. Приведение системы к одноконтурной, определение числовых значений параметров САР.

Структурное преобразование системы корректно начать с преобразования звена с передаточной характеристикой W₁(p) и соответствующим коэффициентом обратной связи β₁. Это объединение на структурной схеме, приведенной ниже, изображено пунктирной линией. Передаточную характеристику преобразованного звена назовем Wэкв1(p).

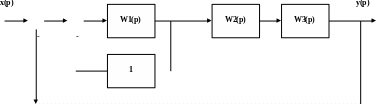
Wэкв1 (p)

Передаточная характеристика Wэкв1(p) равна:

-

-

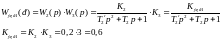
y(p)

x(p)

W₁(p)

Wэкв₁(p)

₁

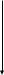
Wэкв2(p)

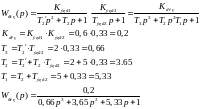
1. 2. Передаточные функции разомкнутой и замкнутой систем.

Передаточная функция разомкнутой системы:

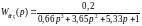
Передаточная функция замкнутой системы:

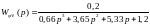
Характеристическое уравнение разомкнутой системы:

Характеристическое уравнение замкнутой системы:

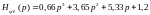
3. Определение статизма системы.

Для оценки качества системы в статике применяют относительную статическую ошибку – статизм, которую определяют как отношение абсолютной статической ошибки к заданному значению регулируемой величины.

;

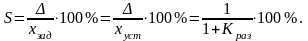
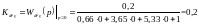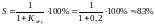
Для работоспособной системы статизм не должен превышать (2 ÷ 5%).

Вывод: данная система в статике неработоспособна, т. к. статизм равен 83%.

2. Исследование замкнутой системы на устойчивость с применением критериев Гурвица, Михайлова и Найквиста.

2. 1. Алгебраический критерий Гурвица.

Алгебраический критерий устойчивости позволяет судить об устойчивости системы по коэффициентам характеристического уравнения.

Система автоматического регулирования устойчива, если все коэффициенты её характеристического уравнения имеют одинаковые знаки, а главный диагональный определитель системы (определитель Гурвица) и его диагональные миноры будут положительными.

Характеристическое уравнение замкнутой системы:

Коэффициенты характеристического уравнения:

; ; ;

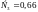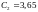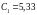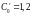
Главный диагональный определитель системы (определитель Гурвица):

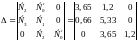
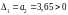
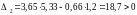
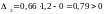
выполняется первое условие (все коэффициенты характеристического уравнения имеют одинаковые знаки).

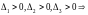выполняется второе условие.

Вывод: замкнутая система устойчива по Гурвицу.

Найдем условие границы устойчивости: