52.Электромагниттік индукция заңы

Фарадейдің электромагниттік индукция заңы.1831 жылғы тәжірибелер негізінде Фарадей ашқан электромагниттік индукция заңын былай тұжырымдауға болады. Кандай себептен болса да тұйық контурмен камтылған ауданды тесіп өтетін магнит индукциясының ағыны өзгеретін болса, контурда электркозғаушы күш пайда болады. Бұл құбылыс кезінде пайда болатын индукциялық ток өзi тудыратын магнит өрісінің бағыты индукциялық токты тудырушы сырткы магнит өpici индукциясының өзгеруіне кepi әсер ететіндей болып бағытталады. Бұл ережені 1833 жылы Э.Х.Ленц ұсынған. Сонымен, электромагниттік индукция заңының жалпы түрде тұжырымдалуының математикалық өрнегі

(11.7)

Электромагниттік индукция заңының дифференциалдық түрі.

Электр козғаушы күшінің аныктамасы бойынша

Сондықтан электромагниттік индукция құбылысы кезінде пайда болатын ЭКК-тi де

(11.8)

түрінде жазуға болады. Ендеше, электромагниттік индукция заңын төмендегідей түрде жазуға болады.

(11.9)

Бұл формуладағы контур L -кез келген тұйык, контур дербес жағдайда индукциялық ток пайда болатын контурмен дәл кeлуі мүмкін. Магнит өpici индукциясының L контурға тірелген бет аркылы алынған ағыны

(11.10)

және L контурмен камтылған аудан уакытқа тәуелді болмайтындыктан,

(11.11)

Соңғы тендіктің сол жағына Стокс теоремасын колдансак

(11.12)

болмаса,

(11.13)

Осы өрнек кез – келген L контурға тірелген бет үшін тепе – теңдік түрде орындалатын болғандықтан, интеграл астындағы өрнек нөлге тең болуы керек

(11.14)

Соңғы тендеу электромагниттік индукция заңының дифферен­циалдық түpi болып табылады. Бұл тендеу Максвелл теңдеулерінің бipi және уакыт бойынша айнымалы магнит өpici құйынды электр өpiciн тудыратынын көрсетеді.

Егер берілген контур аркылы жүретін ток yaқыт бойынша өзгеретін болса, контурмен шектелген ауданды тесіп өтетін магнит ағыны да өзгереді. Олай болса, контурда ЭКК пайда болады. Осы құбылысты өздік индукция деп атайды. Магнит өpici индукциясы токқа , ал магнит ағыны магнит өpici индукциясына пропорционал болғандыктан, контурдағы ток пен онымен камтылатын магнит ағыны бip-бipiнe пропорционал болуы керек

(11.15)

Бұл формулаға кіретін пропорционалдық коэффициент L контурдың индуктивтілігі деп аталады. Индуктивтіліктің бірлігі үшін 1А ток жүрген кезде толық магнит ағынының шамасы 1Вб тең болатын өткізгіштің (контурдың) индуктивтілігі алынады. Бұл бірлікті Генри деп атайды .

Магнит ағыны мен токтың арасындағы тәуелділік ылғи да сызыктық бола бермейді. Мысалы, карастырылып отырған контур ферромагнетикті ортада орналаскан болса, магнит өpici индукциясы ортаның магниттік өтімділігі аркылы магнит өpici кернеулігіне, яғни токка күрделі түрде тәуелді болады. Сондықтан магнит ағыны мен ток арасындағы тәуелділік сызыкты болмайды.

(11.16)

Ток тұракты болған кезде толық магнит ағыны контурдың формасы мен өлшемі өзгерген кезде өзгереді. Олай болса, индуктивтілік контурдың геометриясына және ортаның магниттік касиеттеріне байланысты болады. Егер контурдың геометриясы өзгермейтін болса және ферромагнетик ортада орналаспаған болса, индуктивтілікті тұракты шама деп есептеуге болады.

Мысал ретінде I ток жүретін ұзын соленоидтың индуктивтілігін есептеп көрелік. Соленоидтың ішіндегі магнит өpici кернеулігі

(11.17)

Өздік индукция құбылысы кезінде контурда пайда болатын ЭҚК

(11.18)

Егер тұрақты болса,

(11.19)

53.Термоэлектрлік құбылыстар.Металдардағы және шала өткізгіштердегі жылулық және электрлік құбылыстардың арасында өзара байланыс бар. Мысалы, металда температураның градиентін тудырса, яғни оны біркелкі емес кыздырса, онда жылу ағыны пайда болады. Бұл жылу ағынын тудыруда электрондарда қатысады. Олай болса, біркелкі қыздырылмаған металда электрондардың бағытталған қозғалысы, яғни электрлік ток пайда болады. Температураның градиенті өте үлкен болмағанда пайда болатын ток тығыздығы температура градиентіне тура пропорционал болады . Егер температура градиенті мен қатар электр өpici де нөлден өзге болса

(8.1.1)

мұндағы -металдың электр өткізгіштігі, -металды сипаттайтын жалпы жағдайда температураға тәуелді шама.

Ток тығыздығы сияқты жылу ағынының тығыздығы да тек температура градиенті мен ғана емес, электр өрісімен де анықталады

(8.1.2)

Онзагер және шамалары қатынасымен бip-бipiмeн байланысты екенін көрсеткен.Жоғарыда келтірілген (8.11.1) және (5.11.2) өрнектерін басқаша былай жазуға болады

, (8.1.3)

мұндағы , және . Соңғы формулалардың біріншi өрнегінен өткізгіште ток жоқ кезінде де, егер ол біркелкі қыздырылмаған болса, электр өpici пайда болатынын байқаймыз.

(8.1.4)

Бұл формула біркелкі қыздырылмаған металдарды пайдаланып ЭКҚ көздерін жасауға болатынын көрсетеді. Бipaқ бұл үшін бір металл жеткіліксіз. Ceбeбi ЭКҚ электр өpici кернеулігінен тұйық контур бойымен алынған интеграл болғандықтан

егер тұйық тізбек екі түрлі металдардан тұратын болса, ЭҚК нөлден өзге болады.

54.Скин-эффект, оның заңдылықтары. Тұракты токты карастырған кезде бiз токтың тығыздығы өткізгіштің көлденең кимасы бойынша біркелкі таралады, яғни ток тығыздығы өткізгіштің көлденең кимасының кез келген нүктесінде бірдей мән кабылдайды деп есептеді. Өткізгіш аркылы айнымалы ток жүргенде әр түрлі элементтердің бip-бipiмeн индукциялық өзара әсерлесуі нәтижесінде айнымалы ток тығыздығы өткізгіштің беттік кабаттарында көбірек болады, баскаша айтканда, айнымалы ток өткізгіштің беттік кабаттарында шоғырланады. Бұл құбылысты скин-эффект деп атайды.

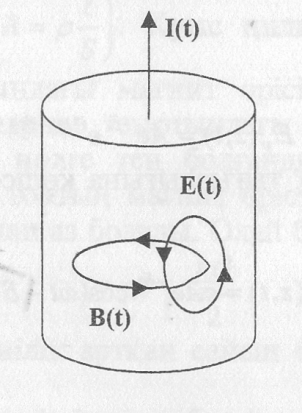Электромагниттік индукция заңы бойынша магнит өрісінің өзгеруі кезінде пайда болатын құйынды электр өpici магнит өpici күш сызыктарын камтып жатуы керек және магнит өрісінің өзгеру бағытымен сол винтті системамен байланысатындыктан, пайда болған құйынды электр өpici өткізгіштің ішкі кабаттарында ток тудырушы өріске карсы, ал беткі кабаттарында онымен бағыттас болады (13.1-сурет). Сондықтан өткізгіштің ішкі кабаттарындағы ток тығыздығы кемиді де, шеткі қабаттарында артады, яғни скин-эффект байқалуға тиісті.

Скин-эффектіні сан жағынан қарастыру үшін 13.1-сурет

өткізгіш ретінде жоғарғы жарты кеңістікті толтыратын ортаны алайық (9.7.2-сурет). Ток заңы, электромагниттік индукция заңын

(13.1)

(13.2)

және локалдык (дифференциалдык) түрде жазылған Ом заңын

(13.3)

пайдаланып электр өpici кернеулігі үшін

(13.4)

теңдеуін табамыз.

Қарастырып отырған ортада және тек Z және t-ға тәуелді болатындықтан, (13.4) тендеуді төмендегідей түрде жазуға болады

(13.5)

Осы тендеудің шешуі,

(13.6)

(13.6) тендеудің ұмтылған кездегі шектелген шегi

(13.7)

мұндағы .

Олай болса

(13.8)

Ом заңын пайдаланып, ток тығыздығына көшсек және накты бөлігін алсақ

(13.9)

55.Диэлектриктердегі электростатикалық өріс.Диэлектриктерде зарядталған еркін бөлшектер жок. Дегенмен, электр өpiciнiң әсерінен диэлектрик молекулаларының құрамына кіретін оң бөлшектер өpic бағытымен, ал тepic бөлшектер өpicкe қарсы жылжиды, сөйтіп әpбip молекула поляризацияланады (полюстер алады). Осының салдарынан диэлектриктің өpicінeн бағыттас жағы оң, қарама-қарсы жағы тepic зарядталады. Бұл құбылысты диэлектриктің поляризациялануы деп атайды. Диэлектриктердің поляризациялануының молекулалық бейнесі. Барлық диэлектриктердің молекулаларының құрамына кіретін оң және тepic зарядтардың центрлері дәл келе бермейді. Сондықтан сыртқы электр өpici жоқ кезде де кейбір диэлектриктердің молекулаларының электрлік моменті болады. Мұндай диэлектриктерді электр өpiciнe орналастырған кезде, оның молекулаларының электрлік моменттері өpic бойымен орналасуға тырысады. Осының нәтижесінде диэлектрик поляризацияланады. Диэлектриктің осындай механизм негізінде поляризациялануын бағытталғыш поляризация, диэлектриктің өзін полярлы диэлектрик деп атайды.Ал егер сыртқы поляризациялаушы өpic жоқ кезінде диэлектрик молекулаларының электрлік моменті нөлге тең болса, ондай диэлектриктерді полярлы емес диэлектриктер деп атайды. Мұндай диэлектриктердің поляризациялануы молекулаларының құрамына кіретін оң және тepic зарядтарының ығысуы нәтижесінде дипольдерге айналуынан болады.

56.Био-Савар-Лаплас заңы. Токтардың магниттік өзара әcepiн зерттеудегі негізгі мәселелердің бipi өткізгіште берілген заңдылықпен таралған токтың туғызатын магнит өpiciн есептеу. Бұл мәселені шешудің екі түрлі жолы бар.Бipiншi жолы жылдамдықпен қозғалатын q зарядтың өзінің маңында туғызатын магнит өpiciн тәжірибе жүзінде зерттей отырып, осы зарядтан қашықтықта орналасқан нүктедегі магнит өpici индукция векторы үшін эмпирикалық әдіспен табылған:

(9.2.1)

формуланы пайдалану. Тогы бар өткізгіштің dV көлеміндегі бәpi жылдамдықпен қозғалатын зарядтардың саны (6.2.1-сурет) Суперпозиция принципі бойьшша осы зарядтардың dv элементтен

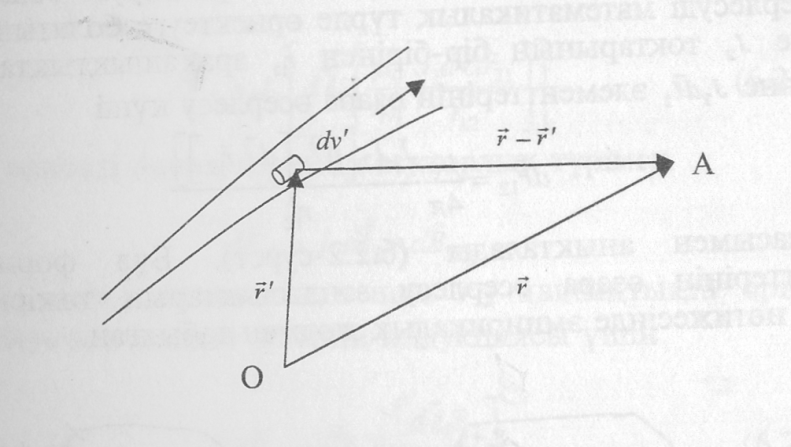
9.2.1-сурет

қашықтықтағы тудыратын магнит өрісінің индукциясын (9.2.1) формуланы пайдаланып есептеуге болады.

(9.2.2)

мұндағы -магнит өpici анықталатын нүктенің радиус-векторы, '-токтың dv элементі орналасқан нүктенің радиус-векторы, элементтен магнит өpici анықталатын нүктеге дейінгі қашықтық. Енді токтың тығыздығы

екенін және оның радиус-векторы нүктедегі мәні алынатындығын ескеріп, (9.2.2) өрнекті былай жазуға болады.

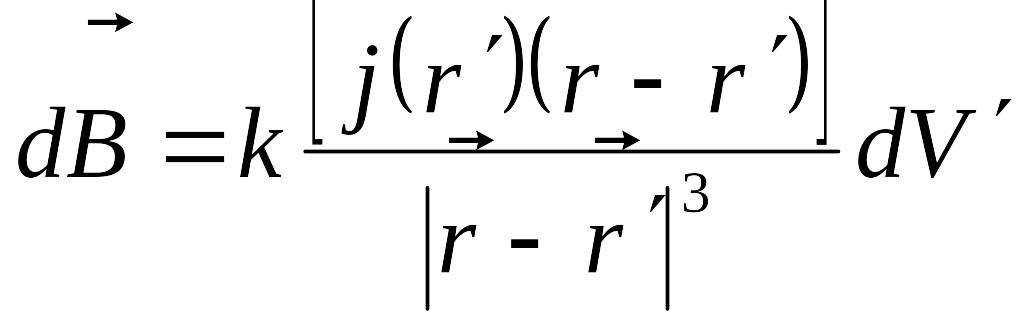(9.2.3)

Тогы бар өткізгіштің алынған нүктедегі туғызатын магнит өpiсі индукция векторын табу үшін, өткізгіш көлемі бойынша интеграл алу керек:

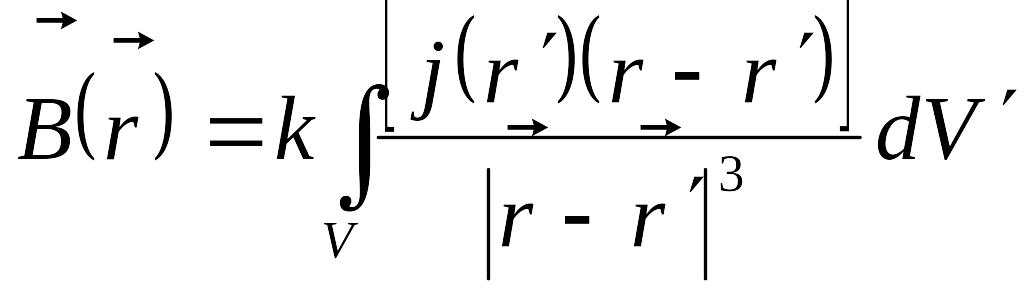(9.2.4)

Егер ток жіңішке сым арқылы жүретін болса, яғни сызықты ток болса -ны ауыстырып, өткізгіш бойымен интеграл алу керек:

(9.2.5)

Екінші жолды Ампер көрсетті. Ампер токтардыц өзара әсерлесу заңдылықтарын зерттей отырып, магниттік өзара әсерлесуін ток элементтерінің өзара әсерлесуі негізінде түсіндіруге болатынын және бұл әсерлесуді математикалық түрде өрнектеуге болатынын көрсет және токтарының бip-бipiнeн арақашықтықта орналасқан және элементтерінің өзара әсерлесу күші

(9.2.6)

формуласымен анықталады (6.2.2-сурет). Бұл формула токтар элементтерінің өзара әсерлесу заңдылықтарын тәжірибе жүзінде зерттеу нәтижесінде эмпирикалық жолмен табылған.

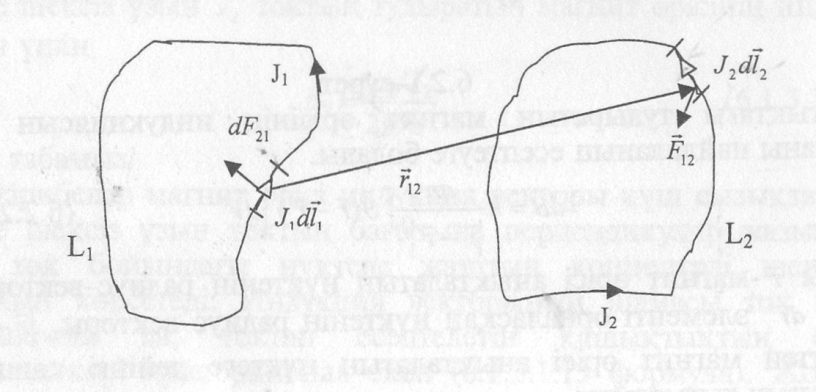
9.2.2 – сурет

Егер (9.2.6) өрнекті элементтің элементке әсерін анықтайтын күшті 1→2 алмастыруының нәтижесінде табуға болады. Жалпы жағдайда және күштер Ньютонның үшінші заңын қанағаттандырмайды контурдағы токтың контурдагы токқа әсер күші

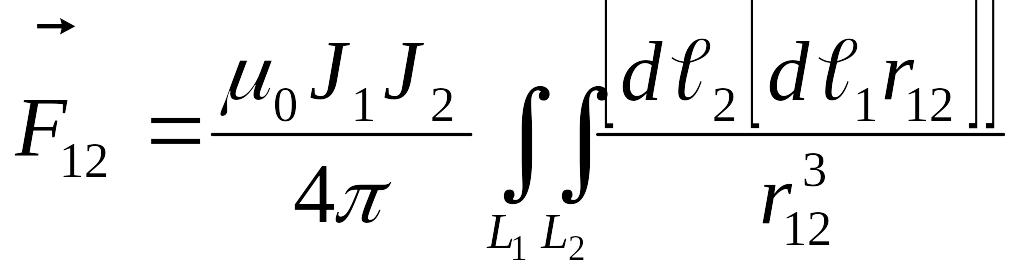(9.2.7)

және контурдағы токтың контурдагы токқа әсер күші

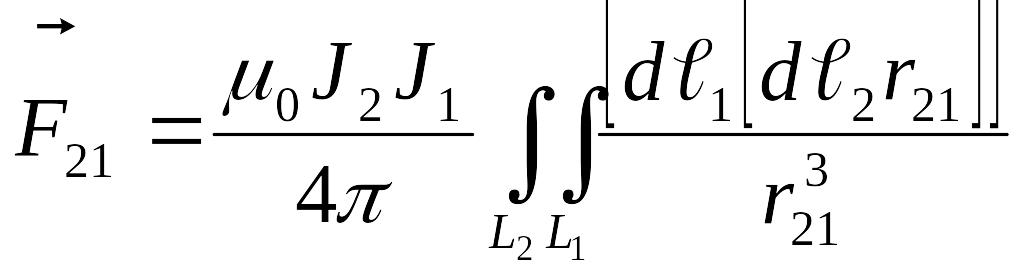
Ньютонның үшінші заңын қанағаттандырады, яғни . Екі ток элементтерінің өзара әсерлесуін бip элемент екінші элемент тұрған нүктеде магнит өpiciн тудырады, осы магнит өpici екінші элементке әсер етеді деп қарастыруға болады. Ол үшін (9.2.6) өрнекті төмендегідей түрде көшіріп жазалық:

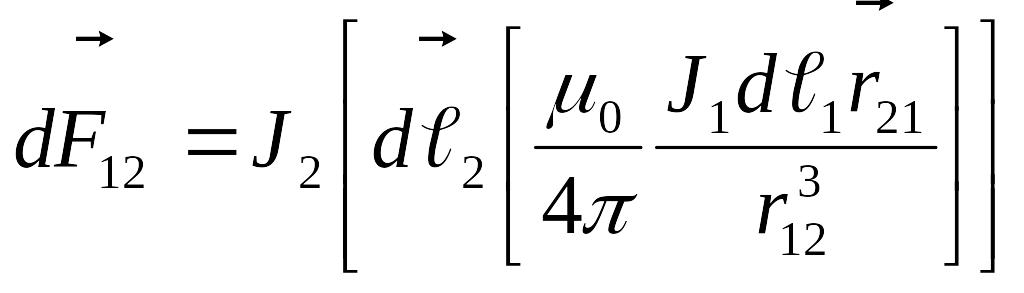(9.2.9)

Енді (9.2.9) өрнекті Ампер күшінің векторльқ түрімен

салыстырып, элементтің өзінен кашықтықта орналасқан нүктеде тудыратын магнит өрісінің индукциясы үшін

(9.2.10)

формуласын табамыз. Бұл формуладғы индекстерді тастап жазсақ және контур бойымен интеграл алсак,

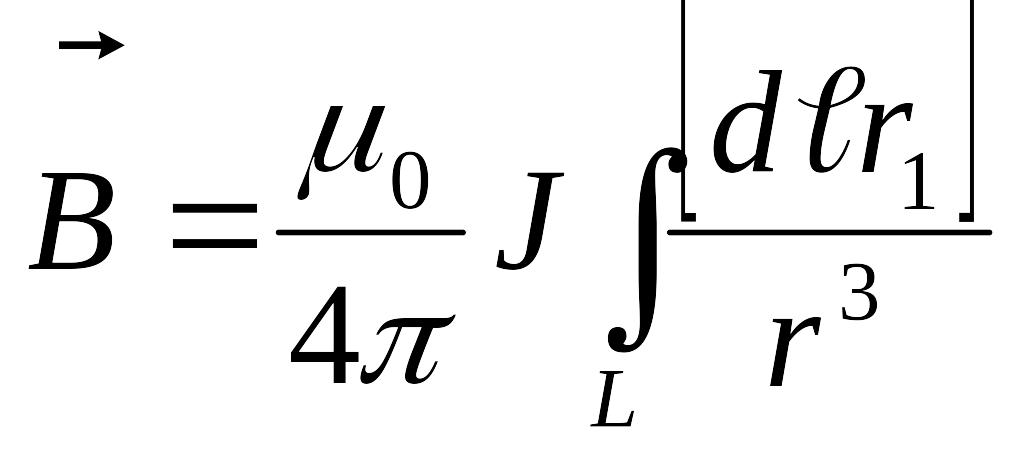(9.2.11)

мұндағы r dl элементтен магнит өpici анықталатын нүктеге дейінгі кашықтық, яғни (9.2.5) өрнектегі -тің мағынасымен бірдей, сондықтан (6.2.11) өрнекті былай көшіріп жазуға болады.

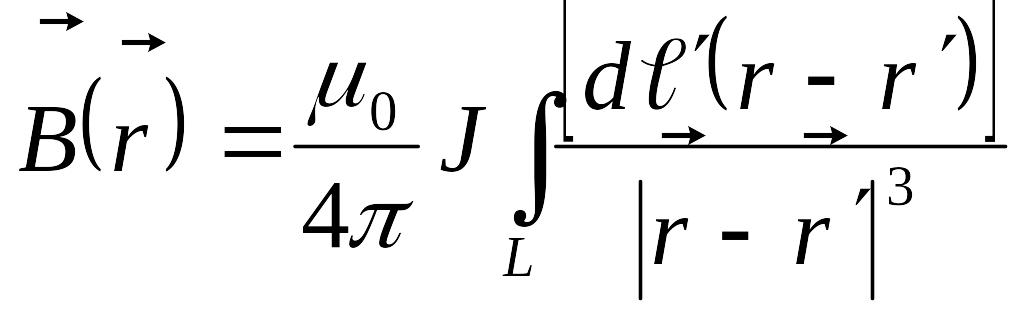(9.2.12)

Соңғы өрнекті (9.2.5) өрнекпен салыстырып, екеніне көз жеткізуге болады. Белгілі заңдылықпен өткізгіште таралған көлемдік токтың, болмаса жіңішке сызыкты токтың тудыратын магнит өpici индукция векторын аныктайтын (9.2.3), (9.2.4) өрнектерді Био-Савар-Лаплас заңы деп атайды.Био-Савар-Лаплас заңының қолданылуы ретінде l ток жүретін ұзындығы ток (өткізгіш) кесіндінің өзінен h кашыктықта тудыратын магнит өрісінің индукция векторын есептелік. (9.2.3-сурет)

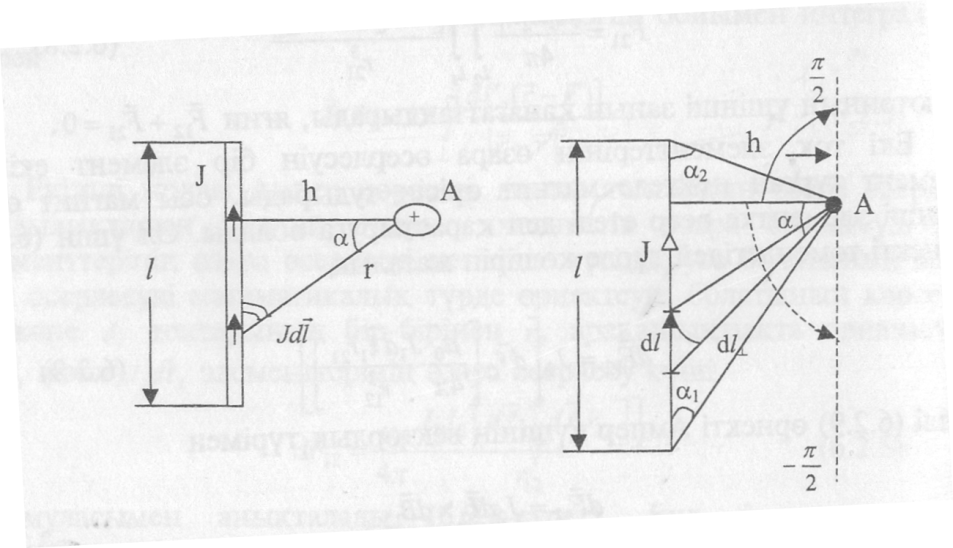
9.2.3-сурет

Био-Савар-Лаплас заңы бойынша (9.2.10) А нүктесіндегі элементтің тудыратын магнит өрісінің бағыты сурет жазыктығына перпендикуляр байкаушыдан әpi карай бағытталған болады және оның шамасы төмендегі өрнекпен анықталады

мұндағы вектор мен векторының арасындағы бұрыш. Жоғарыда келтірілген суреттен , , екенін еске алсак,

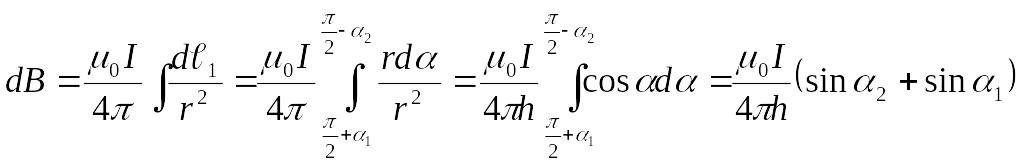(9.2.13)

Бірнеше дербес жағдайлар қарастыралық:

1) Тогы бар өткізгіш жіп шексіз болсын, яғни , . Бұл кезде

Табылған жауап толық әсерді салыстырмалық теориясы тұрғысынан карастырған кездегі жауаппен (9.1.3.15) дәл келеді.

2) Егер А нүктесі тогы бар кесіндінің орта тұсында орналаскан болса,

,