
- •Кулон заңы. Кулон заңының әр түрлі қашықтықтар үшін тәжірибе жүзінде тексерілуі.
- •11. Шала өткізгіштердің электрөткізгіштігі
- •18. Диэлектриктегі электростатикалық өріс үшін Гаусс теоремасы
- •19. Ферми-Дирактың таралуы
- •20. Гаусс теоремасы
- •21.Ток жүрген кезде істелетін жұмыс пен қуат. Джоуль Ленц заңы.
- •27. Ток күші және оның тығыздығы. Зарядтың сақталу заңы.
- •31.Айнымалы бөгде эқк, кедергісі, сыйымдылығы және индуктивтілігі бар тізбек. Импеданс
- •33. Электростатикалық өрістің потенциалдығы.
- •38.Ферромагнетиктердің магниттелу қисығы.Гистерезис тұзағы.
- •Синхронды және асинхронды двигательдердің жұмыс істеу принциптері
- •44.Тұрақты электр өрісі
- •45.Заттың плазмалық күйі. Плазма
- •46.Өзара индукция құбылысы
- •47.Өткізгіштердегі электростатикалық өріс
- •48.Кирхгоф ережелері
- •49.Стационар токтың магнит өрісі
- •50.Электростатикалық өріс энергиясы
- •51.Тәуелсіз газ разрядтары түрлері
- •52.Электромагниттік индукция заңы
- •57.Диэлектростатикалық өріс энергиясы.
- •Диамагнетиктердің магниттелу механизмі
- •Полярлы емес диэлектриктер
- •62.Электромагниттік индукция
- •Электромагниттік индукция заңының дифференциалдық түрі
- •65.Өзара индукция құбылысы
- •66.Сұйық заттардың электр өткізгіштігі
- •73.Газдық разрядтар түрлері
- •75.Магнетиктер түрлері
- •77.Диамагнетиктердің магниттелу механизмі (Ерболат)
Кулон заңы. Кулон заңының әр түрлі қашықтықтар үшін тәжірибе жүзінде тексерілуі.
Кулон заңы. Өзара әсерлесетін зарядтарды нүктелік зарядтар деп есептеу үшін, олардың алып жатқан көлемдерінің орта өлшемі зарядтың бip-бipiнeн қашықтығына қарағанда өте аз болуы керек. Осындай екі зарядтың өзара әсерлесу күші заряд шамаларының көбейтіндісіне тура пропорционал да, арақашықтығының квадратына кepi пропорционал екендігін Ш. О. Кулон 1785 жылы тікелей тәжірибелер негізінде дәлелдеген:
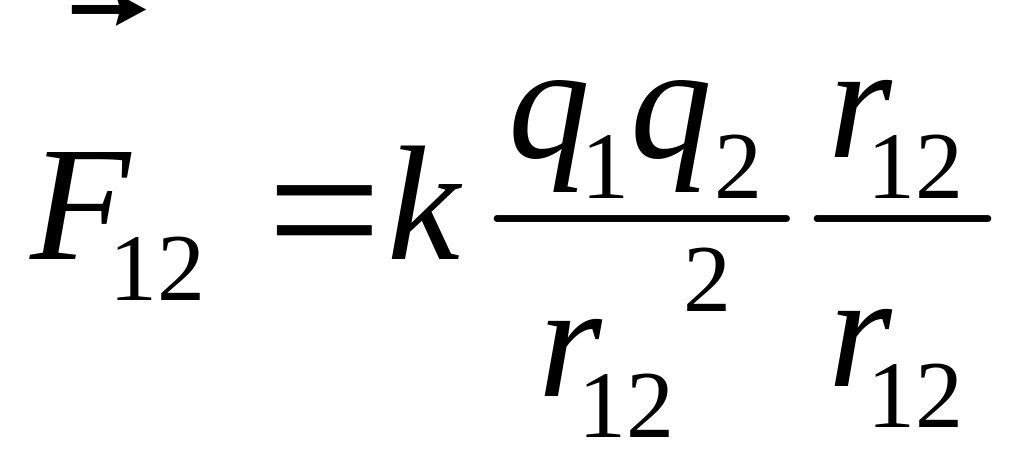 (2.2.1)
(2.2.1)
мұндағы
![]() - екі зарядты қосатын түзудің бойымен
бағытталған бірлік вектор,k - бірліктер
системасына байланысты пропорционалдық
коэффициент. СИ системасында k=8,9875
- екі зарядты қосатын түзудің бойымен
бағытталған бірлік вектор,k - бірліктер
системасына байланысты пропорционалдық
коэффициент. СИ системасында k=8,9875![]()
Көпшілік
жағдайда
![]() түрінде алады, ендеше
түрінде алады, ендеше
![]() вакуумның электрлік өтімділігі деп
аталады. (2.2.1) формуладан
вакуумның электрлік өтімділігі деп
аталады. (2.2.1) формуладан
![]() екенін
байқау қиын емес.
екенін
байқау қиын емес.
2.2.1. Кулон заңыныц әр түрлі
кашықтықтар үшін тәжірибе жүзінде
тексерілуі. Кавендиш
әдісі. Кулон заңын
тексерудің әдісін 1772
жылы ұсынған Кавендиш
болды. Егер күш арақашықтықтың квадратына
кepi пропорционал болса, заряд шардың
беткі қабатында орналасады, ceбeбi шар
көлемінде заряд болса, кез келген шар
қабатына оның iшкi жағында сфералы
симметриялық түрде таралған зарядтар
тарапынан күш әсер етіп, ондағы зарядтар
шар бетіне қарай ығысар еді. Ал егер күш
Кулон заңына бағынбайтын болса, онда
заряд шар көлемінде де таралуы керек.
Осы жағдайды пайдалана отырып, Кавендиш
![]() -ның
мәнi 0,02-ден кіші екенін көрсеткен. Кулон
заңының
-ның
мәнi 0,02-ден кіші екенін көрсеткен. Кулон
заңының
![]() арақашықтықтарға
дейін дұрыс екендігін Резерфорд
тәжірибелері көрсетіп, ал энергиясы
бірнеше электрон-вольт электрондардың
серпімді шашырауын зерттеу нәтижесінде
Кулон заңы
арақашықтықтарға
дейін дұрыс екендігін Резерфорд
тәжірибелері көрсетіп, ал энергиясы
бірнеше электрон-вольт электрондардың
серпімді шашырауын зерттеу нәтижесінде
Кулон заңы
![]() арақашықтықтарға дейін дұрыстығын
дәлелдеу үшін, кванттық физиканың
қағидаларын пайдалану керек.
арақашықтықтарға дейін дұрыстығын
дәлелдеу үшін, кванттық физиканың
қағидаларын пайдалану керек.
Электр өрісіндегі күштер Зарядтардың өзара әсерлесетінін білeмiз. Олардың әсерлесу күшін принципінде Кулон заңын пайдаланып есептеуге болады. Бipaқ тәжірибеде кеңістікте белгілі бip заңдылықпен таралған электр өрісінің зарядтарға әсерін есептеуге тура келеді. Сондықтан берілген электр өрісіндегі зарядтарға ісер ететін күштерді қарастырамыз.
Нүктелік
зарядка әсер ететін күш.
Кеңістікте белгілі бip заңдылықпен
таралған өpic болса, оны кернеулікпен
![]() сипаттауға болады. Осы өрістегі q нүктелік
зарядка әсер ететін күш заряд орналасқан
нүктедегі өрістің кернеулігінің мәні
мен заряд шамасының көбейтіндісіне
тең:
сипаттауға болады. Осы өрістегі q нүктелік
зарядка әсер ететін күш заряд орналасқан
нүктедегі өрістің кернеулігінің мәні
мен заряд шамасының көбейтіндісіне
тең:
![]() (5.5.1.1)
(5.5.1.1)
егер өpic
біркелкі болса
![]() ,
онда нүктелік зарядқа әсер ететін күш
тұрақты болады
,
онда нүктелік зарядқа әсер ететін күш
тұрақты болады
![]() (5.5.1.2)
(5.5.1.2)
Дипольге әсер ететін күш. Дипольдің анықтамасы бойынша, оның құрамына кіретін зарядтарға әсер ететін күштердің геометриялық қосындысы
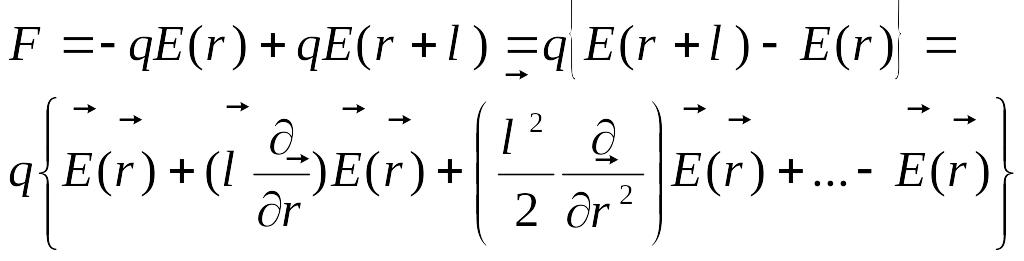 (5.5.2.1)
(5.5.2.1)
Дипольдің
иінi өте кіші шама болғандықтан
![]() оның аумағында өpic кернеулігінің өзгepyi
әлсіз деп есептеуге болады, сондықтан
екінші peттi аз шамаларды ескермесек
(5.5.2.1) формуланы былай жазуға болады:
оның аумағында өpic кернеулігінің өзгepyi
әлсіз деп есептеуге болады, сондықтан
екінші peттi аз шамаларды ескермесек
(5.5.2.1) формуланы былай жазуға болады:
![]() (5.5.2.2)
(5.5.2.2)
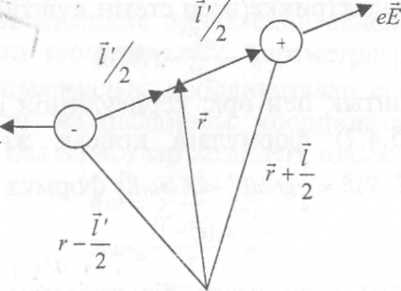 Сонымен
дипольге әсер ететін күш тек біртекті
емес электр өpiciнe ғана нөлден өзге және
оның диполь осінің бойымен өзгеру
жылдамдығына тәуелді. Егер өpic біртекті
болса,
Сонымен
дипольге әсер ететін күш тек біртекті
емес электр өpiciнe ғана нөлден өзге және
оның диполь осінің бойымен өзгеру
жылдамдығына тәуелді. Егер өpic біртекті
болса,
![]() ,
өйткені диполь зарядтарына әсер ететін
күштер шама жағынан тең де, бағыттары
қарама-қарсы. Сыртқы электр өрісінде
дипольге оның центріне қарағанда күш
моменті әсер етеді (5.5.2.1-сурет).
,
өйткені диполь зарядтарына әсер ететін
күштер шама жағынан тең де, бағыттары
қарама-қарсы. Сыртқы электр өрісінде
дипольге оның центріне қарағанда күш
моменті әсер етеді (5.5.2.1-сурет).
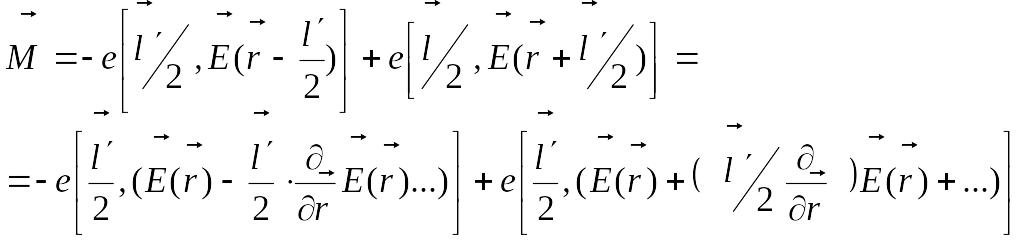 Tepic зарядқа
әсер ететін күштің иінін анықтайтын
вектор 5.5.2.1-сурет
Tepic зарядқа
әсер ететін күштің иінін анықтайтын
вектор 5.5.2.1-сурет
F
![]() және
екінші peттi аз шамаларды еске алмасақ.
және
екінші peттi аз шамаларды еске алмасақ.
![]() (5.5.4.3)
(5.5.4.3)
Бұл
формуладан сыртқы өріске қойылған
дипольдің электрлік моменті
![]() өpic кернеулігінің бағытына параллель
болуға тырысады.
өpic кернеулігінің бағытына параллель
болуға тырысады.
Үзіліссіз
таралған зарядқа әсер ететін күш.
Өрісте орналасқан дене бойымен
![]() көлемдік тығыздыкпен таралған зарядка
әсер ететін күшті табу үшін суперпозиция
принципін пайдаланамыз. Ол үшін алдымен
дененің
көлемдік тығыздыкпен таралған зарядка
әсер ететін күшті табу үшін суперпозиция
принципін пайдаланамыз. Ол үшін алдымен
дененің
![]() элементіне әсер ететін күшті табамыз.
Бұл элементтің заряды
элементіне әсер ететін күшті табамыз.
Бұл элементтің заряды
![]() болғандықтан, оған әсер ететін күш:
болғандықтан, оған әсер ететін күш:
![]()
Зарядталған дененің бірлік көлеміне, әсер ететін шама, яғни күштің көлемдік тығыздығы:
![]()
онда
![]() (5.5.3.1)
(5.5.3.1)
Диэлектрикке
әсер ететін көлемдік күштер.
Электр өрісінде орналасқан диэлектриктің
бірлік көлеміне әсер ететін күшті табу
үшін де, суперпозиция принципін
пайдаланамыз. Диэлектриктің dV элементінің
электрлік моменті
![]() -поляризацияланғыштық.
Енді осы элементті диполь деп қарастырып,
(5.5.2.2) формуланы қолдансақ:
-поляризацияланғыштық.
Енді осы элементті диполь деп қарастырып,
(5.5.2.2) формуланы қолдансақ:
![]() (5.5.4.1)
(5.5.4.1)
Соңғы өрнектен диэлектрикке әсер ететін күштің көлемдік тығыздығы
![]() (5.5.4.2)
(5.5.4.2)
Поляризацияланғыштық
пен өpic кернеулігінің арасындағы
![]() қатынасын (5.5.4.2) формулаға қойсақ
қатынасын (5.5.4.2) формулаға қойсақ
![]() формуласын ескерсек
формуласын ескерсек
![]() (5.5.4.2)
(5.5.4.2)
(5.5.4.2)
формуланы алар кезде бiз диэлектриктің
поляризациялану коэффициенті
![]() координатаға тәуелді емес деп есептедік.
Бұл жағдай диэлектрик созылған және
сығылғанда жеке молекулалардың
поляризациялану коэффициенттері
өзгермейтін диэлектриктер үшін
орындалады. Мұндай шарттар көбінесе
газдар мен сұйықтарда орындалады.
координатаға тәуелді емес деп есептедік.
Бұл жағдай диэлектрик созылған және
сығылғанда жеке молекулалардың
поляризациялану коэффициенттері
өзгермейтін диэлектриктер үшін
орындалады. Мұндай шарттар көбінесе
газдар мен сұйықтарда орындалады.
Сонымен
![]() үлкен екенін еске алсақ, сыртқы өріске
қойылған диэлектрикке электр өpici
кернеулігінің модулі
үлкен екенін еске алсақ, сыртқы өріске
қойылған диэлектрикке электр өpici
кернеулігінің модулі
![]() жылдам өзгеретін жаққа қарай бағытталған
күш әсер ететінін байқаймыз, нәтижесінде
диэлектрик осы бағытқа қарай итерілуі
керек. Заряд өткізгіштің бетімен таралды.
Оның ds
беттік элементінің заряды
жылдам өзгеретін жаққа қарай бағытталған
күш әсер ететінін байқаймыз, нәтижесінде
диэлектрик осы бағытқа қарай итерілуі
керек. Заряд өткізгіштің бетімен таралды.
Оның ds
беттік элементінің заряды
![]() .
Осы элемент орналасқан нүктедегі ds
элементтен тыс жатқан зарядтардың өpic
кернеулігі
.
Осы элемент орналасқан нүктедегі ds
элементтен тыс жатқан зарядтардың өpic
кернеулігі
![]() .
Олай болса,
.
Олай болса,
![]() .
Өткізгіштің бірлік бетіне әсер ететін
күш
.
Өткізгіштің бірлік бетіне әсер ететін
күш
![]() ,
,
![]() -өткізгіш
бетіне перпендикуляр жүргізілген
бірлік вектор.
-өткізгіш
бетіне перпендикуляр жүргізілген
бірлік вектор.
Күш моменті M=e[l E (r)]=[P E (r)]
Магнетиктердің магнит өріс Магнетиктер деп сырткы магнит өpiciн өзгерте, болмаса өздігінен магнит өpiciн тудыра алатын ортаны айтады. Магнетиктер негізінен үш топқа: -диа, -пара, -ферро магнетиктерге бөлінеді. Диамагнетиктерге сырткы магнит өpici жок, кезінде атомдарының магниттік моменттері нөлге тең магнетиктер жатады. Парамагнетиктерге сырткы магнит өpici жок кезінде атомдарының(молекулаларының) магниттік моменттepi нөлге тең емес бipaқ физикалык, аз көлемінің магниттік моменті нөлге тең магнетиктер жатады. Ферромагнетиктерге сырткы магнит өpici жок кезінде де макроскопиялық облыстарының (домендерінің) магниттікмоменттepi нөлге тең емес, бipaқ қалыпты жағдайда тұтас магниттелген күйде болмайтын магнетиктер жатады.
Магнетиктердің магниттелуін сан жағынан сипаттау үшін магниттелгіштік деген шама ендіріледі.Бұл магниттелген магнетиктің физикалық аз көлеміндегі молекулалардың магниттік моменттерінің геометриялық (векторлық) осы көлемге катынасымен анықталады
![]() (9.5.20)
(9.5.20)
мұндағы
![]() -физикалық
аз көлемнің шамасы, Р -молекулалардың
магниттік моменттері, косынды
көлемге кіретін барлық молекулаларды
камтиды. Баскаша айтканда, магниттелгіштік
магнетиктің бірлік көлемінің магниттік
моменті, яғни магнетиктің магниттік
моментінің көлемдік тығыздығы. Олай
болса,
көлемнің магниттік моменті
-физикалық
аз көлемнің шамасы, Р -молекулалардың
магниттік моменттері, косынды
көлемге кіретін барлық молекулаларды
камтиды. Баскаша айтканда, магниттелгіштік
магнетиктің бірлік көлемінің магниттік
моменті, яғни магнетиктің магниттік
моментінің көлемдік тығыздығы. Олай
болса,
көлемнің магниттік моменті
![]()
Магнетиктердегі
өpic. Сонымен
магнетиктердегі магнит өpici өткізгіштік
токтар тудыратын өpic В мен магнетиктердің
магниттелуі кезінде пайда болатын
молекулалық токтар тудыратын өрістің
(В') косындысынан тұрады, яғни
![]() .
.
Қандай токтың болса да тудыратын магнит өpici күш сызықтарының тұйык болатындығынан
![]() (9.5.22)
(9.5.22)
Олай болса, магнетиктердегі магнит өpici де тұйық бет бойымен алынған ағыны нөлге тең болады екен.
Скаляр потенциал. Нүктелік зарядтың және оның жүйесіндегі, үзіліссіз таралған зарядтың потенциалы. Скалярлық потенциал. Электростатикалық өрістің потенциалдығын (2.3.1)ө өрнектен А12 жұмысты басқа бір шаманың айырмасы ретінде жазуға болатындығын байқауға болады.Ш Шынында, А12=W1-W2, мұндағы
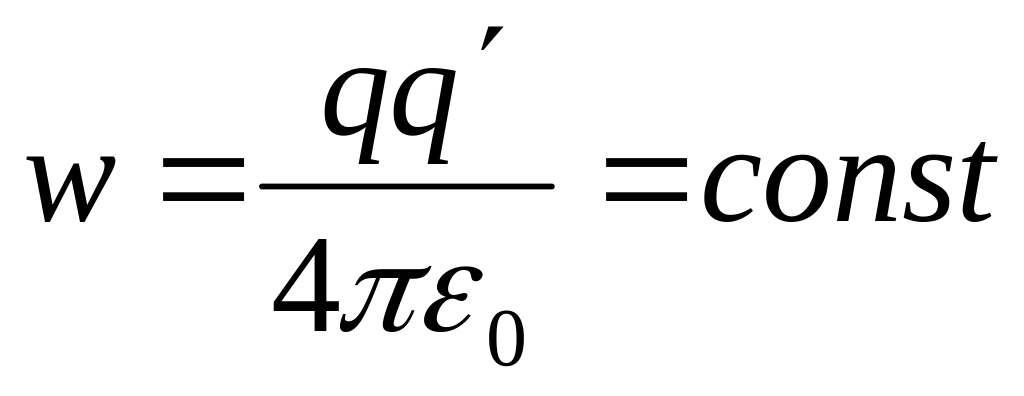 екі
нүктелік зарядтардың өзара әсерлесуінің
энергиясы.
екі
нүктелік зарядтардың өзара әсерлесуінің
энергиясы.
![]()
![]() (2.3.1.1)
(2.3.1.1)
Соңғы
өрнектен
![]() нүктелік зарядты бір нүктеден екінші
нүктеге көшірген кезде істелетін
жұмыстың осы заряд шамасына қатынасы
тек q нүктелік зарядтың шамасына және
одан жүргізілген радиус векторлардың
шамаларына байланысты екенін байқаймыз.
Ендеше,
зарядтың туғызатын электростатикалық
өрісін сипаттайтын тағы бір көмекші
шама
нүктелік зарядты бір нүктеден екінші
нүктеге көшірген кезде істелетін
жұмыстың осы заряд шамасына қатынасы
тек q нүктелік зарядтың шамасына және
одан жүргізілген радиус векторлардың
шамаларына байланысты екенін байқаймыз.
Ендеше,
зарядтың туғызатын электростатикалық
өрісін сипаттайтын тағы бір көмекші
шама
![]() скалярлық потенциалды енгізуге болады.
Бұл шаманы зарядтардың өзара әсерлесу
потенциалдық энергиясының
зарядына қатынасымен анықтайды, яғни
скалярлық потенциалды енгізуге болады.
Бұл шаманы зарядтардың өзара әсерлесу
потенциалдық энергиясының
зарядына қатынасымен анықтайды, яғни
![]() (2.3.1.2)
(2.3.1.2)
Ендеше
А12=
![]()
Егер (2.3.1.2) өрнектің екі жағына да grad операторымен әсер етсек:
![]() ,
яғни
,
яғни
![]() =-
=-![]() (2.3.1.3)
(2.3.1.3)
Электростатикалық өрістің күштік сипаттамасы кернеулік пен оның энергетикалық сипаттамасы скалярлық потенциал өзара (2.3.1.3) өрнегімен байланысқан.
Нүктелік зарядтың және оның жүйесіндегі, үзіліссіз таралған зарядтың потенциалы.
Нүктелік зарядтың нормаланған потенциалы (2.3.2.1) формуламен анықталады.
![]() (2.3.2.1) формула.
(2.3.2.1) формула.
Нүктелік зарядтар системасының потенциалын табу үшін нүктелік заряд потенциалының формуласын және суперпозиция принципін пайдалану керек.
![]() (2.3.3.1)
(2.3.3.1)
Бұл
формуладағы
![]() -
потенциалы анықталып отырған нүктенің
радиус- векторы,
-
потенциалы анықталып отырған нүктенің
радиус- векторы,
![]() -і-ші
нүктелік заряд орналасқан нүктенің
радиус-векторы.
-і-ші
нүктелік заряд орналасқан нүктенің
радиус-векторы.
Заряд
белгілі бір көлем бойынша
![]() тығыздықпен үзіліссіз таралған болса,
заряд таралған көлемнің әрбір бөлігін
нүктелік заряд ретінде қарастыруға
боларлықтай етіп қте кішкентай бөліктерге
бөлеміз. Сонда, әр бөлігінің заряды dq1=
тығыздықпен үзіліссіз таралған болса,
заряд таралған көлемнің әрбір бөлігін
нүктелік заряд ретінде қарастыруға
боларлықтай етіп қте кішкентай бөліктерге
бөлеміз. Сонда, әр бөлігінің заряды dq1=
![]() d
d![]() болады.
Енді суперпозиция принципін пайдаланып
және өте кішкентай көлемдер бойынша
алынған қосындының шегі интегралға тең
екенін ескерсек,
болады.
Енді суперпозиция принципін пайдаланып
және өте кішкентай көлемдер бойынша
алынған қосындының шегі интегралға тең
екенін ескерсек,
![]() (2.3.3.2)
(2.3.3.2)
болып шығады.
Диэлектриктер. Диэлектриктер деп калыпты жағдайда құрамында еркін зарядталған бөлшектер болмайтын, ток өткізбейтін заттарды айтады. Диэлектриктер негізінен үш топқа: полярлы, полярлы емес, сегнетоэлектриктер болып үш топқа бөлінеді.Диэлектриктерде зарядталған еркін бөлшектер жок. Дегенмен, электр өpiciнiң әсерінен диэлектрик молекулаларының құрамына кіретін оң бөлшектер өpic бағытымен, ал тepic бөлшектер өpicкe қарсы жылжиды, сөйтіп әpбip молекула поляризацияланады (полюстер алады). Осының салдарынан диэлектриктің өpicінeн бағыттас жағы оң, қарама-қарсы жағы тepic зарядталады. Бұл құбылысты диэлектриктің поляризациялануы деп атайды.
Барлық диэлектриктердің молекулаларының құрамына кіретін оң және тepic зарядтардың центрлері дәл келе бермейді. Сондықтан сыртқы электр өpici жоқ кезде де кейбір диэлектриктердің молекулаларының электрлік моменті болады. Мұндай диэлектриктерді электр өpiciнe орналастырған кезде, оның молекулаларының электрлік моменттері өpic бойымен орналасуға тырысады. Осының нәтижесінде диэлектрик поляризацияланады. Диэлектриктің осындай механизм негізінде поляризациялануын бағытталғыш поляризация, диэлектриктің өзін полярлы диэлектрик деп атайды.
Ал егер
сыртқы поляризациялаушы өpic жоқ кезінде
диэлектрик молекулаларының электрлік
моменті нөлге тең болса, ондай
диэлектриктерді полярлы
емес диэлектриктер
деп атайды. Поляризацияланған диэлектриктің
тудыратын электр өpiciн сан жағынан
сипаттау үшін поляризацияланғыштық
деген шама ендіріледі. Бұл шама
поляризацияланған диэлектриктің бірлік
көлемінің электрлік моментімен
анықталады, яғни бірлік көлемдегі
молекулалардың электрлік моменттерінің
геометриялық қосындысына тең:
![]() мұндағы
мұндағы
![]() -
молекуланың электрлік моменті, n -бірлік
көлемдегі молекулалар саны. Кейде
поляризацияланғышты поляризацияланған
диэлектриктің
-
молекуланың электрлік моменті, n -бірлік
көлемдегі молекулалар саны. Кейде
поляризацияланғышты поляризацияланған
диэлектриктің
![]() көлемінің
көлемінің
![]() электрлік моментінің осы көлемге
қатынасының
электрлік моментінің осы көлемге
қатынасының
![]() шегі ретінде де анықтайды:
шегі ретінде де анықтайды:
![]()
Полярлы
емес диэлектрик біртекті болса, оның
молекулаларының сыртқы өpic әсерінен
алған электрлік моменттері
![]() бірдей болады. Сондықтан
бірдей болады. Сондықтан
![]() (4.1.3)
(4.1.3)
Егер сыртқы өpic өте үлкен болмаса, молекуланың индукцияланған электрлік моменті өpic кернеулігіне пропорционал деп есептеуте болады:
![]() ,
,
![]() (4.1.4)
(4.1.4)
мұндағы
z-диэлектриктің поляризацияланғыштық
коэффициенті
немесе диэлектрлік
коэффициенті
деп аталады. Полярлы емес диэлектриктер
үшін а молекулалардың поляризацияланғыштық
коэффициенттерінің қосындысына тең:
![]()
Ол үшін
электрлік моменті
молекуланы (дипольді) кернеулігі
өріске қойған кезде, молекуланың қосымша
w=-
энергия алатынын және оның мәніне қарай
молекула сандарының өзгеруі Больцман
таралуына бағынатынын еске аламыз
![]() ,
,
![]()
өрнегіне
кіретін А тұрақтыны табу үшін оны
sin![]() d
-ға
көбейтіп,
арқылы
-ден
d
-ға
көбейтіп,
арқылы
-ден
![]() -гe
дейін интеграл аламыз. Бұл интеграл
бірлік көлемдегі электрлік моменттерінің
бағыттары
-гe
дейін интеграл аламыз. Бұл интеграл
бірлік көлемдегі электрлік моменттерінің
бағыттары
![]() аралығында
жататын молекулалардың санына
аралығында
жататын молекулалардың санына
![]() тең болады
тең болады
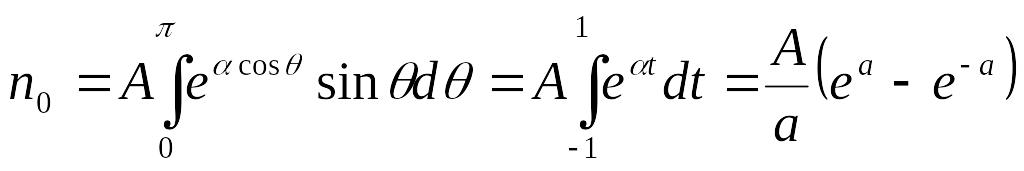
![]() .
Сонымен электрлік моменттерінің бағыты
өpic кернеулігінің бағытымен
бұрыш жасайтын бірлік көлемдегі
молекулалардың саны
.
Сонымен электрлік моменттерінің бағыты
өpic кернеулігінің бағытымен
бұрыш жасайтын бірлік көлемдегі
молекулалардың саны
![]()
Поляризацияланған диэлектриктің бірлік көлемінің электрлік моменті
![]() (4.1.7)
(4.1.7)
мұндағы
![]() -
Ланжевен
функциясы деп
аталады.
-
Ланжевен
функциясы деп
аталады.
Электростатикалық өpic энергиясы. Электростатикалық өpicтe зарядты бip нүктеден екінші нүктеге көшірген кезде жұмыс жасалатынын білеміз. Бұл жұмыс өpicті тудырушы зарядтардың өзара әсерлесуін сипаттайтын потенциалдык энергия.
Дискретті зарядтар системасының өзара әсерлесу энергиясы.
Алдымен екі
нүктелік
зарядтардан тұратын
системаны қарастыралық.
Нүктелік
зарядтар бip-бipінен
шексіз
кашықтықта
орналасқан
кезде олардың
өзара
әсерлесу
энергиясын нөлге
тең
(әсерлеспейді).
Егер кеңістіктің
белгілі бip
нүктесінде
орналасқан
![]() зарядтан
зарядтан
![]() кашыктықтағы
нүктеге
кашыктықтағы
нүктеге
![]() зарядты шексіздіктен
көшірген
кезде істелетін
жұмыс
(2.3.1) формулаға
сәйкес
зарядты шексіздіктен
көшірген
кезде істелетін
жұмыс
(2.3.1) формулаға
сәйкес
![]()
![]() (5.1.2)
(5.1.2)
мұндағы
![]() заряд көшіріліп әкелетін нүктедегі
зарядтың потенциалы. Бұл жұмыс системаның
потенциалдық энергиясын өзгертеді.
және
әр аттас зарядтар болса, системаның
потенциалдық энергиясы кемиді, ал аттас
болса артады. Зарядталған бөлшектер
бip-бipiнeн шексіздікте орналасқан кездегі
системаның потенциалдық энергиясы
нөлге тең болғандыктан
заряд көшіріліп әкелетін нүктедегі
зарядтың потенциалы. Бұл жұмыс системаның
потенциалдық энергиясын өзгертеді.
және
әр аттас зарядтар болса, системаның
потенциалдық энергиясы кемиді, ал аттас
болса артады. Зарядталған бөлшектер
бip-бipiнeн шексіздікте орналасқан кездегі
системаның потенциалдық энергиясы
нөлге тең болғандыктан
![]() және
және
![]() жұмыстар системаның потенциалдық
энергиясына тең, яғни
жұмыстар системаның потенциалдық
энергиясына тең, яғни
![]() (5.1.3)
(5.1.3)
(5.1.3) өрнекті пайдаланып,
![]() (5.1.4)
(5.1.4)
Егер
шексіздіктен тағы бip
![]() нүктелік зарядын
зарядтан
нүктелік зарядын
зарядтан
![]() нүктеге, ал
зарядтан
нүктеге, ал
зарядтан
![]() нүктеге шексіздіктен көшіріп әкелсек
нүктеге шексіздіктен көшіріп әкелсек
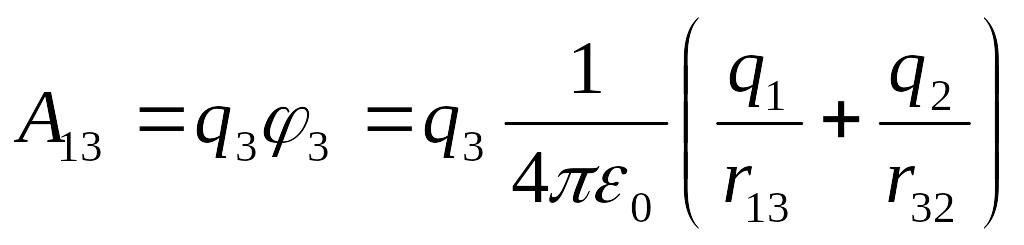 (5.1.5)
(5.1.5)
жұмыс
жасалады. Мұндағы
![]() заряд көшіріліп әкелген нүктедегі
және
зарядтардың потенциалы.
заряд көшіріліп әкелген нүктедегі
және
зарядтардың потенциалы.
![]() және
және
![]() жұмыстарының қосындысы системаның
потенциалдық энергиясына тең болады.
жұмыстарының қосындысы системаның
потенциалдық энергиясына тең болады.
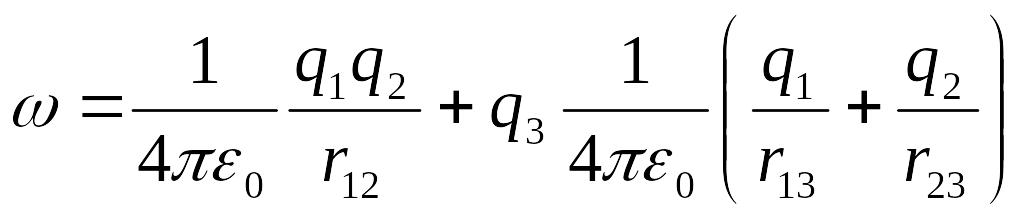 (5.1.6)
(5.1.6)
Соңғы теңдікті төмендегідей түрде түрлендіріп, жазуға болады
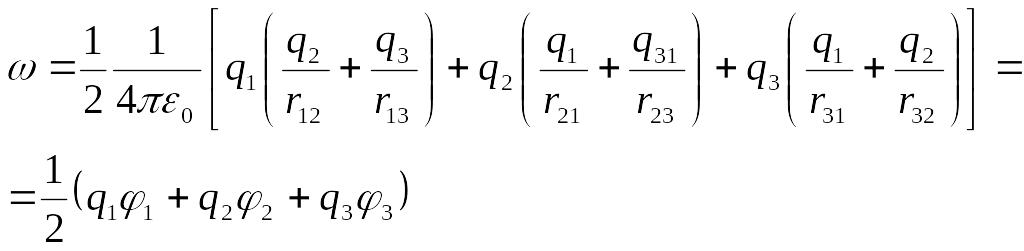 (5.1.7)
(5.1.7)
Егер
системаның құрамында n
нүктелік заряд болғанша
![]() ,
,
![]() т.с.с. зарядтармен толықтыра берсек,
оның потенциалдық энергиясы:
т.с.с. зарядтармен толықтыра берсек,
оның потенциалдық энергиясы:
![]() (5.1.8)
(5.1.8)
мұндағы
![]() нүктелік заряд орналасқан нүктедегі
басқа зарядтардың тудыратын потенциалы.
нүктелік заряд орналасқан нүктедегі
басқа зарядтардың тудыратын потенциалы.
Үзіліссіз таралған зарядтың потенциалдық энергиясы.
Көлемі
![]() көлемдік тығыздықпен зарядталған дене
берілсін. Зарядталған көлемді әpбip
бөлігін нүктелік заряд ретінде қарастыруға
болатындай етіп ұсақ dV
бөліктерге бөлеміз, әpбip бөлігінің
заряды dq
= pdV.
Енді dq
зарядтар системасына (5.1.8) формуланы
қолдансақ және қосындыдан интегралға
көшсек.
көлемдік тығыздықпен зарядталған дене
берілсін. Зарядталған көлемді әpбip
бөлігін нүктелік заряд ретінде қарастыруға
болатындай етіп ұсақ dV
бөліктерге бөлеміз, әpбip бөлігінің
заряды dq
= pdV.
Енді dq
зарядтар системасына (5.1.8) формуланы
қолдансақ және қосындыдан интегралға
көшсек.
![]() (5.2.1)
(5.2.1)
Егер зарядтар бет арқылы таралған болса (5.2.2-сурет).
![]() (5.2.2)
(5.2.2)
Егер зарядтар көлем және бет арқылы таралған болса
![]() (5.2.3)
(5.2.3)
(5.2.3) формуладағы - барлық көлемдік және беттік зарядтардың dV, элементіндегі туғызатын потенциалы. (5.1.8) және (5.2.3) формулалардың бip-бipiнeн айырмашылығы (5.1.8) формулада зарядтардың меншікті энергиясы, яғни бip зарядтың әр түрлі бөліктерінің бip-бipiмeн әcepi, ескерілмейді, ceбeбi зарядтар нүктелерде шоғырланған деп есептеледі. Ал (5.2.3) формула зарядталған денелер системасының (дененің) толық энергиясын анықтайды.
7.
Тұйық тізбек үшін Ом заңы.
Сыртқы R кедергі мен ішкі кедергісі
![]() ток көзінен тұратын тұйық тізбек
қарастырайық.
ток көзінен тұратын тұйық тізбек
қарастырайық.
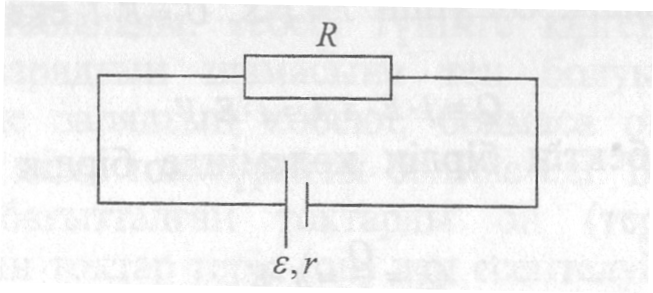
6.4.6.1-сурет
(6.4.5.6)
формуланы тұйық тізбек үшін қолдансақ
![]() ,
,
![]() (6.4.6.1)
(6.4.6.1)
мұндағы
![]() - тұйық тізбектегі кернеудің толык түcyi
- сыртқы R және ішкі
- тұйық тізбектегі кернеудің толык түcyi
- сыртқы R және ішкі
![]() кедергілердегі кернеулердің түсулерінің
алгебралық қосындысы:
кедергілердегі кернеулердің түсулерінің
алгебралық қосындысы:
![]() .
Тізбектің бөлігі үшін Ом заңы бойынша
.
Тізбектің бөлігі үшін Ом заңы бойынша
![]() ,
,
![]() .
Онда
.
Онда
![]() ,
болмаса
,
болмаса
![]() (6.4.6.2)
(6.4.6.2)
Соңғы тендік тұйық тізбек үшін Ом заңы болып табылады. Бұл заң бойынша, тұйық тізбектегі ток күші тізбектегі ЭҚК-ке пропорционал да, сыртқы және ішкi кедергілердің қосындысына кepi пропорционал.
8.Фарадейдің электромагниттік индукция заңы.1831 жылғы тәжірибелер негізінде Фарадей ашқан электромагниттік индукция заңын былай тұжырымдауға болады. Кандай себептен болса да тұйық контурмен камтылған ауданды тесіп өтетін магнит индукциясының ағыны өзгеретін болса, контурда электркозғаушы күш пайда болады. Бұл құбылыс кезінде пайда болатын индукциялық ток өзi тудыратын магнит өрісінің бағыты индукциялық токты тудырушы сырткы магнит өpici индукциясының өзгеруіне кepi әсер ететіндей болып бағытталады. Бұл ережені 1833 жылы Э.Х.Ленц ұсынған. Сонымен, электромагниттік индукция заңының жалпы түрде тұжырымдалуының математикалық өрнегі
![]() (11.7)
(11.7)
Электромагниттік индукция заңының дифференциалдық түрі.
Электр
козғаушы күшінің аныктамасы бойынша
![]()
Сондықтан электромагниттік индукция құбылысы кезінде пайда болатын ЭКК-тi де
(11.8)
түрінде жазуға болады. Ендеше, электромагниттік индукция заңын төмендегідей түрде жазуға болады.
![]() (11.9)
(11.9)
Бұл формуладағы контур L -кез келген тұйык, контур дербес жағдайда индукциялық ток пайда болатын контурмен дәл кeлуі мүмкін. Магнит өpici индукциясының L контурға тірелген бет аркылы алынған ағыны
![]() (11.10)
(11.10)
және L контурмен камтылған аудан уакытқа тәуелді болмайтындыктан,
![]() (11.11)
(11.11)
Соңғы тендіктің сол жағына Стокс теоремасын колдансак
![]() (11.12)
(11.12)
болмаса,
![]() (11.13)
(11.13)
Осы өрнек кез – келген L контурға тірелген бет үшін тепе – теңдік түрде орындалатын болғандықтан, интеграл астындағы өрнек нөлге тең болуы керек
![]() (11.14)
(11.14)
Соңғы тендеу электромагниттік индукция заңының дифференциалдық түpi болып табылады. Бұл тендеу Максвелл теңдеулерінің бipi және уакыт бойынша айнымалы магнит өpici құйынды электр өpiciн тудыратынын көрсетеді.Егер берілген контур аркылы жүретін ток yaқыт бойынша өзгеретін болса, контурмен шектелген ауданды тесіп өтетін магнит ағыны да өзгереді. Олай болса, контурда ЭКК пайда болады. Осы құбылысты өздік индукция деп атайды. Магнит өpici индукциясы токқа , ал магнит ағыны магнит өpici индукциясына пропорционал болғандыктан, контурдағы ток пен онымен камтылатын магнит ағыны бip-бipiнe пропорционал болуы керек
![]() (11.15)
(11.15)
Бұл
формулаға кіретін пропорционалдық
коэффициент L
контурдың индуктивтілігі
деп аталады. Индуктивтіліктің бірлігі
үшін 1А
ток жүрген кезде толық магнит ағынының
шамасы 1Вб
тең болатын өткізгіштің (контурдың)
индуктивтілігі алынады. Бұл бірлікті
Генри деп атайды
![]() .
Магнит ағыны мен токтың арасындағы
тәуелділік ылғи да сызыктық бола
бермейді. Мысалы, карастырылып отырған
контур ферромагнетикті ортада орналаскан
болса, магнит өpici индукциясы ортаның
магниттік өтімділігі аркылы магнит
өpici кернеулігіне, яғни токка күрделі
түрде тәуелді болады. Сондықтан магнит
ағыны мен ток арасындағы тәуелділік
сызыкты болмайды.
.
Магнит ағыны мен токтың арасындағы
тәуелділік ылғи да сызыктық бола
бермейді. Мысалы, карастырылып отырған
контур ферромагнетикті ортада орналаскан
болса, магнит өpici индукциясы ортаның
магниттік өтімділігі аркылы магнит
өpici кернеулігіне, яғни токка күрделі
түрде тәуелді болады. Сондықтан магнит
ағыны мен ток арасындағы тәуелділік
сызыкты болмайды.
![]() (11.16)
(11.16)
Ток тұракты болған кезде толық магнит ағыны контурдың формасы мен өлшемі өзгерген кезде өзгереді. Олай болса, индуктивтілік контурдың геометриясына және ортаның магниттік касиеттеріне байланысты болады. Егер контурдың геометриясы өзгермейтін болса және ферромагнетик ортада орналаспаған болса, индуктивтілікті тұракты шама деп есептеуге болады.Мысал ретінде I ток жүретін ұзын соленоидтың индуктивтілігін есептеп көрелік. Соленоидтың ішіндегі магнит өpici кернеулігі
![]() (11.17)
(11.17)
Өздік индукция құбылысы кезінде контурда пайда болатын ЭҚК
![]() (11.18)
(11.18)
Егер тұрақты болса,
![]() (11.19)
(11.19)
Өзара индукция құбылысы. Катар орналаскан екі контурлардың біріндегі ток өзгерген кезде, екіншісі тесіп өтетін магнит ағыны өзгереді, яғни индукцияланған электр козғаушы күші пайда болады. Осы құбылысты өзара индукция құбылысы деп атайды.
9.Конденсаторлар және олардың сыйымдылығы.Конденсатор деп арасындағы кеңістікке сыртқы өрістің әcepi болмайтын етіп орна-ластырылған екі өткізгіштен тұратын системаны айтады. Өткізгіштер конденсатордың астарлары деп аталады және олар шамалары тең таңбалары қарама-қарсы зарядталады. Астарларының түріне қарай конденсаторларды жазық, цилиндрлік және сфералық деп бөледі. Конденсатордың сыйымдылығы оның астарларына берілген зарядтың астарларының арасындағы потенциалдар айырымының қатынасымен анықталады:

![]()
Жазық
конденсатор
деп жақын орналастырылған екі жазық
өткізгіштен (пластинадан) тұратын
системаны айтады (2.4.9.1.1-сурет). Конденсатор
астарларының арасындағы кеңістікке
сыртқы өрістің әcepi болмауы үшін
![]() шарты орындалуы керек және осы шарт
орындалғанда астарлар арасындағы өpicтi
біртекті деп есептеуге болады.Өрістің
кернеулігі
шарты орындалуы керек және осы шарт
орындалғанда астарлар арасындағы өpicтi
біртекті деп есептеуге болады.Өрістің
кернеулігі
![]() -ға
тең болады. Ал астарлар арасындағы
потенциал айырымы, өріс біртекті
болғандықтан
-ға
тең болады. Ал астарлар арасындағы
потенциал айырымы, өріс біртекті
болғандықтан
![]() Сыйымдылықтың
анықтамасы бойынша
Сыйымдылықтың
анықтамасы бойынша
![]()
 Цилиндрлік
конденсатордың астарлары
концентрлі цилиндрлер болады. Цилиндрлік
конденсатор үшін
Цилиндрлік
конденсатордың астарлары
концентрлі цилиндрлер болады. Цилиндрлік
конденсатор үшін
![]() болуы керек. Радиусы
болуы керек. Радиусы
![]() аралығында жататын цилиндрлік бетке
Гаусс теоремасын қолданып, конденсатор
астарларының арасындағы өpic кернеулігін
табамыз (2.4.9.2.1-сурет). Бұл кезде
аралығында жататын цилиндрлік бетке
Гаусс теоремасын қолданып, конденсатор
астарларының арасындағы өpic кернеулігін
табамыз (2.4.9.2.1-сурет). Бұл кезде
![]() шартты пайдаланып, өpic кернеулігі цилиндр
өсіне перпендикуляр бағытталған деп
есептейміз.
шартты пайдаланып, өpic кернеулігі цилиндр
өсіне перпендикуляр бағытталған деп
есептейміз.
![]() ,
,
![]()
Енді
![]() қатынасын пайдалансақ:
қатынасын пайдалансақ:
![]()
Соңғы теңдіктен,
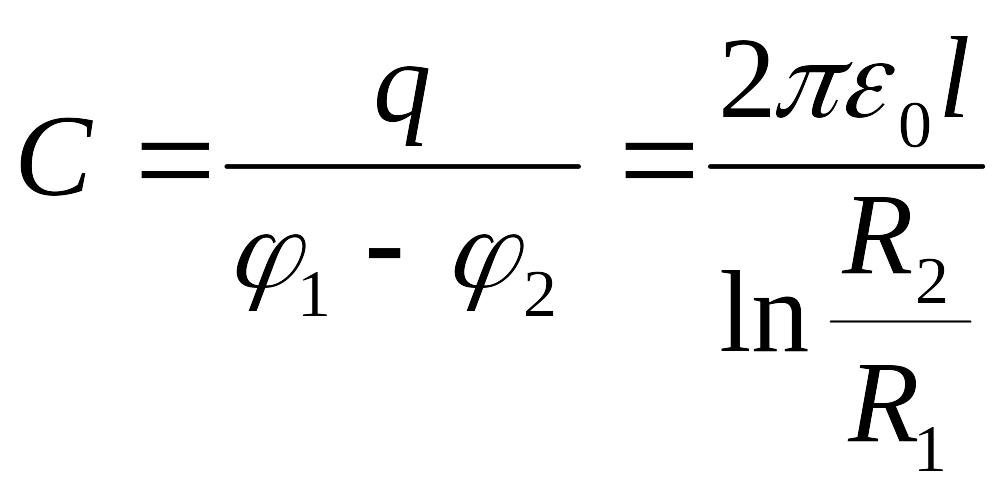
Сфералық конденсатор сыйымдылығының алдыңғы екі пункттердегі әдісті пайдаланып
![]()
болатынын
көрсету керек. Сонымен қатар цилиндрлік
және сфералық конденсаторлар
сыйымдылықтарының
![]() ,
кезде жазық конденсатор сыйымдылығына
ұмтылатына көз жеткізу керек.
,
кезде жазық конденсатор сыйымдылығына
ұмтылатына көз жеткізу керек.
10.Сегнетоэлектриктер
мен пьезоэлектриктер.
Диэлектриктердің ерекше тобы
сегнетоэлектриктер болып табылады.
Қалыпты жағдайда сегнетоэлектриктердің
домендер деп аталатын физикалық аз
көлемінің электрлік моменті нөлден
өзге болады, бipaқ сегнетоэлектрик тұтас
поляризацияланбаған болады.
Сегнетоэлектриктерге сегнет тузы
![]() барий титанаты
барий титанаты
![]() жатады. Сегнетоэлектриктердің басқа
диэлектриктерден тағы да айырмашылығы
олардың диэлектриктік өтімділігі өте
үлкен бірнеше мыңға дейін жетеді,
электрлік ығысу векторы мен өpic кернеулігі
арасындағы байланыс сызықты емес, яғни
диэлектриктік өтімділік кернеулікке
тәуелді және электрлік ығысу векторының
белгілі бip уакыттағы мәні кернеуліктің
осы уакыт алдындағы мәндерінің қандай
болғанына да байланысты.
жатады. Сегнетоэлектриктердің басқа
диэлектриктерден тағы да айырмашылығы
олардың диэлектриктік өтімділігі өте
үлкен бірнеше мыңға дейін жетеді,
электрлік ығысу векторы мен өpic кернеулігі
арасындағы байланыс сызықты емес, яғни
диэлектриктік өтімділік кернеулікке
тәуелді және электрлік ығысу векторының
белгілі бip уакыттағы мәні кернеуліктің
осы уакыт алдындағы мәндерінің қандай
болғанына да байланысты.
Сегнетоэлектриктегі электрлік ығысу векторы мен кернеулік арасындағы байланысты тәжірибе түрінде тексергенде бұл байланыстың сызыкты емес екендігін тағайындалды. Ол үшін (6.3.1-суретте) келтірілген электрлік схеманы пайдалануға болады.
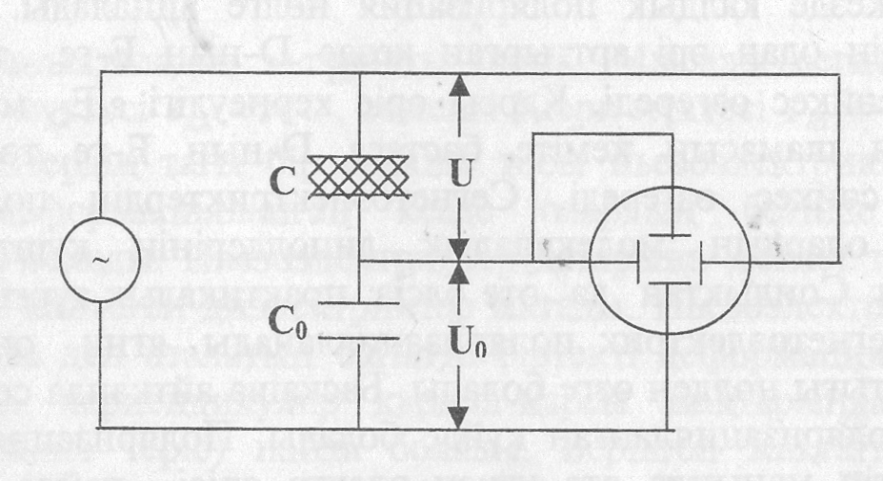
6.3.1-сурет
Г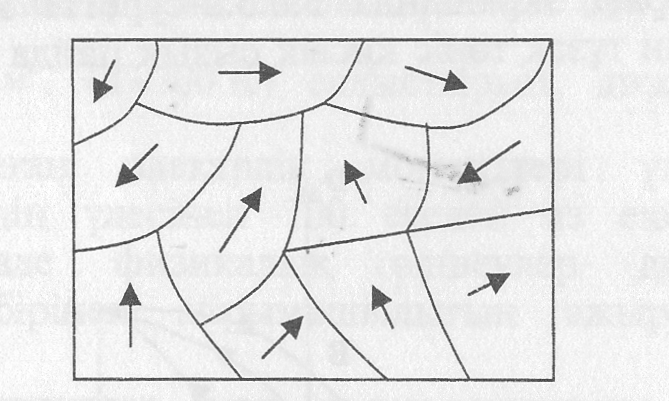
 енератордың
гармоникалық заңдылықпен өзгеретін
кepнeyi
енератордың
гармоникалық заңдылықпен өзгеретін
кepнeyi
![]() және
және
![]() кондесаторлар арасында
кондесаторлар арасында
![]() және
және
![]() кернеулерге бөлінеді. Осы кернеулерді
схемада керсетілгендей етіп осциллограф
пластиналарына қоссақ, осциллограф
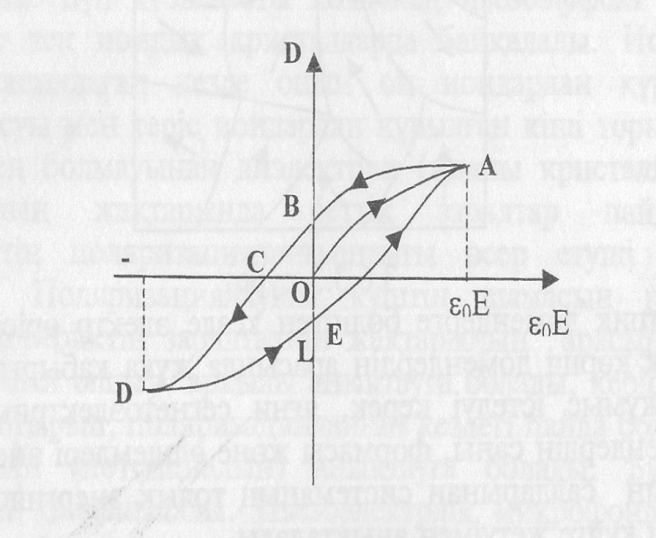
экранында 6.3.2-суретте көрсетілгендей
гистерезис
деп аталатын тұзақ теріс қисық сызық
пайда болады.Тұтас поляризацияланбаған
сегнетоэлектрикті сыртқы өріске қойған
кезде сегнетоэлектрик OA қисығына сәйкес
поляризацияланады. Егер кернеулік Е
кернеулерге бөлінеді. Осы кернеулерді
схемада керсетілгендей етіп осциллограф
пластиналарына қоссақ, осциллограф
экранында 6.3.2-суретте көрсетілгендей
гистерезис
деп аталатын тұзақ теріс қисық сызық
пайда болады.Тұтас поляризацияланбаған
сегнетоэлектрикті сыртқы өріске қойған
кезде сегнетоэлектрик OA қисығына сәйкес
поляризацияланады. Егер кернеулік Е![]() мәніне жеткеннен кейін оның шамасын
кеміте бастаса D мен Е арасындағы байланыс
АО бойымен емес ABCD бағытымен өзгереді,
яғни D-ның мәндері Е-нің мәндеріне
қарағанда қалып өзгереді. Кернеулік
нөлге тең болған кезде D-ның мәні ОВ
кесіндінің шамасымен анықталады.
Электрлік ығысу векторының бұл мәнін
қалдық поляризация деп атайды. Қалдық
поляризацияны нөлге айналдыру үшін
бастапкы өpicкe қарама-қарсы бағытталған
өpic тудыру керек. Осы қарсы өрістің
кернеулігінің мәні ОС кесінді шамасына
тең болған кезде қалдық поляризация
нөлге айналады. Өpic кернеулігінің
мәнін одан әpi арттырған кезде D-ның Е-ге
тәуелділігі CD қисығына сәйкес өзгереді.
Қарсы өpic кернеулігі
мәніне жеткеннен кейін оның шамасын
кеміте бастаса D мен Е арасындағы байланыс
АО бойымен емес ABCD бағытымен өзгереді,
яғни D-ның мәндері Е-нің мәндеріне
қарағанда қалып өзгереді. Кернеулік
нөлге тең болған кезде D-ның мәні ОВ
кесіндінің шамасымен анықталады.
Электрлік ығысу векторының бұл мәнін
қалдық поляризация деп атайды. Қалдық
поляризацияны нөлге айналдыру үшін
бастапкы өpicкe қарама-қарсы бағытталған
өpic тудыру керек. Осы қарсы өрістің
кернеулігінің мәні ОС кесінді шамасына
тең болған кезде қалдық поляризация
нөлге айналады. Өpic кернеулігінің
мәнін одан әpi арттырған кезде D-ның Е-ге
тәуелділігі CD қисығына сәйкес өзгереді.
Қарсы өpic кернеулігі
![]() мәніне жеткен кезде оның шамасын кеміте
бастаса D-ның Е-ге тәуелділігі DLA кисығына
сәйкес өзгереді. Сегнетоэлектриктердің
поляризациялану механизмі олардың
молекулалык, диполдерінің күшті
әсерлесуіне байланысты. Сондықтан да
өте әлсіз практикалық, тұрғыдан нөлге
тең өрісте де сегнетоэлектрик
поляризацияланады, яғни оның
поляризацияланғыштығы нөлден өзге
болады. Басқаша айтқанда сегнетоэлектрик
өздігінен поляризацияланған күйде
болады.
мәніне жеткен кезде оның шамасын кеміте
бастаса D-ның Е-ге тәуелділігі DLA кисығына
сәйкес өзгереді. Сегнетоэлектриктердің
поляризациялану механизмі олардың
молекулалык, диполдерінің күшті
әсерлесуіне байланысты. Сондықтан да
өте әлсіз практикалық, тұрғыдан нөлге
тең өрісте де сегнетоэлектрик
поляризацияланады, яғни оның
поляризацияланғыштығы нөлден өзге
болады. Басқаша айтқанда сегнетоэлектрик
өздігінен поляризацияланған күйде
болады.
Поляризацияланған
сегнетоэлектрикті маңында өте үлкен
электр өpici пайда болады, бірақ
сегнетоэлектриктің энергиясы
термодинамикалык тепе-тендік күйде
мүмкін болғанша аз болуы керек, сондықтан
сегнетоэлектрик тұтас поляризацияланбай,
электрлік моменттері нөлден өзге
макроскопиялық көлемдерге-домендерге
бөлініп кетеді (6.3.3-сурет). Сегнетоэлектрик
домендерге бөлінген кезде электр
өрісінің энергиясы азаяды,
бipaқ көршi домендердің арасында жұқа
қабырға (қалқа) пайда болу үшін жұмыс
істелуі керек, яғни сегнетоэлектриктің
энергиясы артады. Домендердің саны,
формасы және өлшемдері энергияның кемуі
мен артуының салдарынан системаның
толық энергиясы ең аз мәнін қабылдайтын
күйге жетуімен анықталады.Сегнетоэлектрик
ылғи да поляризацияланған күйде қала
бермейді. Әpбip сегнетоэлектрик температура
белгілі бip
![]() мәнінен асқан кезде өзінің сегнетоэлектриктік
қасиеттерін жоғалтып, кәдімгі полярлы
диэлектрикке айналады. Бұл
температураны Кюри
нүктeci
деп атайды. Keйбіp сегнетоэлектриктердің
екі Кюри нүктесі болады.
мәнінен асқан кезде өзінің сегнетоэлектриктік
қасиеттерін жоғалтып, кәдімгі полярлы
диэлектрикке айналады. Бұл
температураны Кюри
нүктeci
деп атайды. Keйбіp сегнетоэлектриктердің
екі Кюри нүктесі болады.
Температура, белгілі бip Кюри нүктесінің маңында сегнетоэлектриктің поляризацияланғыштың коэффициентінің температураға тәуелділігі
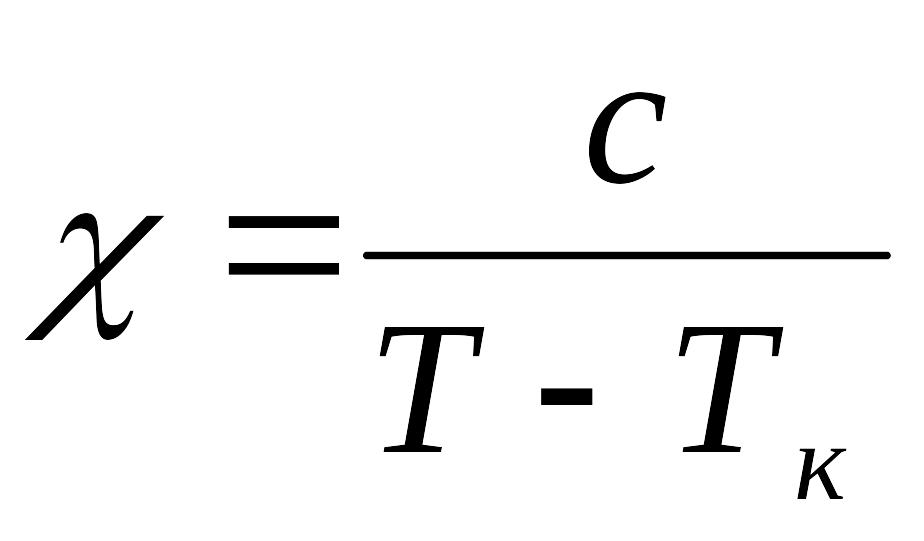 (6.3.1)
(6.3.1)
заңдылыкпен
анықталады.
с -
тұрақты
шама. Мысалы сегнет тұзының
жоғарғы
Кюри нүктeci
![]() ,
төменгі
Кюри нүктесі
,
төменгі
Кюри нүктесі
![]() .
.
