2. Средняя собственная информация (энтропия) Энтропия

Дискретный источник удобнее характеризировать количеством собственной информации, содержащимся в среднем в одном символе ансамбля X.

Это среднее количество собственной информации есть

I(X)=M[ –log p(X)]= (8)

и названо энтропией.

Основные свойства энтропии

1. Энтропия неотрицательна

H(X)  0. (9)

Знак равенства имеет место, когда X – не случайна, т.е. p(x_j)=1, а p(x_i)= 0 для i  j. При этом неопределенность относительно ансамбля X отсутствует. Т.о., энтропия есть мера неопределенности случайного ансамбля.

2. Величина энтропии удовлетворяет неравенству

H(X)  log n. (10)

Знак равенства имеет место при равновероятности символов ансамбля Х, т.е. при p(x_j)=1/n.

3. Свойство аддитивности энтропии.

В последовательности n независимых символов энтропия равна сумме энтропий, содержащихся в отдельных символах

H[X⁽¹⁾, …, X⁽ⁿ⁾]=H(X⁽¹⁾) + …+ H(X⁽ⁿ⁾). (11)

Вычисление энтропии по формуле (8) можно упростить, введя функцию

(p) = –p log p, тогда формула примет вид

. (12)

Условная энтропия

Пусть имеются два статистически зависимых конечных ансамбля символов X и Y. Пары символов x_jy_k с вероятностями p(x_j , y_k) можно рассматривать как элементарные символы объединенного ансамбля X Y с энтропией

(13)

Появление символа x_jX вызовет появление символа y_kY с условной вероятностью

При этом условная энтропия ансамбля Y в предположении, что выбран символ x_j будет

(14)

Здесь каждому x_j соответствует свое значение энтропии H(Y/x_j), т.е. H(Y/x_j) – случайная величина

Тогда средняя условная энтропия случайной величины Y, вычисленная при условии, что известно значение другой случайной величины X, равна

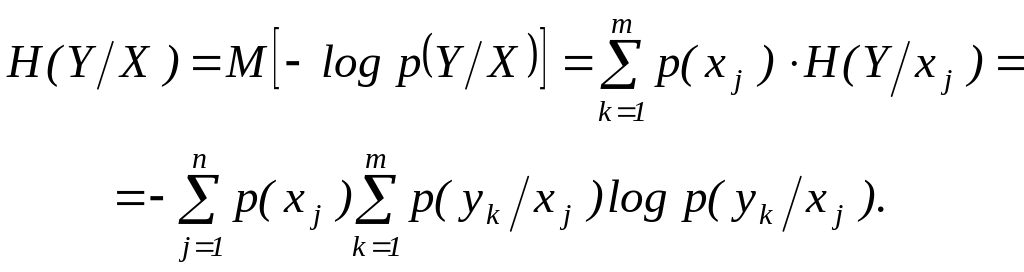(15)

Энтропия объединенного ансамбля H (XY) удовлетворяет следующим соотношениям:

а) H (XY) = H (X) + H (Y/ X) = H (Y) + H (X/ Y) , (16) если X и Y зависимы;

б) H (XY) = H (X) + H (Y), если X и Y независимы. (17)

Для объединенного ансамбля XY условная энтропия удовлетворяет неравенствам:

H (Y/ X)  H (Y), (18)

H (X/ Y)  H (X).

Избыточность

Считают, что имеется избыточность, если количество информации, содержащейся в сигнале (энтропия сигнала), меньше того количества, которое этот сигнал мог бы содержать по своей физической природе. Ведем количественную меру избыточности.

Пусть сигнал длиной в n символов (отсчетов) содержит количество информации H. Пусть далее наибольшее количество информации, которое в принципе может содержаться в данном сигнале с учетом наложенных на него ограничений (заданное основание кода, заданная средняя мощность сигнала и т.п.), равно H_max. Иногда количественной мерой избыточности является величина

(19)

Причины появления избыточности – это статистическая связь между символами (отсчетами) сигнала и неэкстремальность распределения вероятностей отдельных символов (отсчетов). Введение избыточности приводит к удлинению сигнала, но зато повышает его информационную устойчивость при воздействии помех.

Задачи для решения в аудитории.

Пример 1.

На измерительной станции имеются два прибора. Первый имеет шкалу, содержащую100 делений, его показания могут меняться через каждые 0,05 с. Шкала второго прибора имеет 10 делений, и его показания могут меняться каждые 0,01 с.

Какова наибольшая средняя информация, поставляемая двумя приборами в 1 секунду?

Решение.

1-й прибор.

Энтропия одного значения (отсчета) по формуле (10)

H₁(X)=log m₁=log 100.

Число отсчетов в 1 с n₁=1/0,05=20.

2-й прибор.

Энтропия одного значения (отсчета) по формуле (10)

H₂(X)=log m₂=log 10.

Число отсчетов в 1 с n₂=1/0,01=100.

Энтропия двух приборов в 1 с по формуле (11)

H_[X]=n₁ H₁ (X) + n₂ H₂ (X)=20 log₂ 00 + 100 log₂10 =

= 20*6.64+100*3.32  465 бит, с

Пример 2.

Производится стрельба по двум мишеням, по одной сделано 2 выстрела, по второй – 3. Вероятности попадания при одном выстреле соответственно равны ½ и ¹/₃. Исход стрельбы (число попаданий) по какой мишени является более определенным, если число попаданий в мишень подчинено биномиальному закону распределения

p(X=m)=C_n^m p^m (1–p) ^n–m , где

Cnm =	n!
	m!(n –m)!

Составим ряд распределения для числа попаданий в первую мишень при n=2 и р=¹/₂

m	0	1	2
Cnm	1	2	1
pm	1	1/2	1/4
(1–p) n–m	1/4	1/2	1
p(X=m)	1/4	1/2	1/4

и вторую мишень при n=3 и р=¹/₃

m	0	1	2	3
Cnm	1	3	3	1
pm	1	1/3	1/9	1/27
(1–p) n–m	8/27	4/9	2/3	1
p(X=m)	8/27	4/9	2/9	1/27

Мерой неопределенности исхода стрельбы служит энтропия числа попаданий. Энтропия числа попаданий при стрельбе по первой мишени

	m1
H1(X)= –		p(xj) log p(xj)=
	j=1

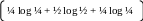
= – = 1+ 0,5 = 1,5 бит.

По второй мишени

	m2
H2(X)= –		p(xj) log p(xj)=
	j=1

= – =

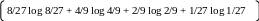
= 1,7 бит.

Сравнивая H₁(X) и H₂(X), получаем

H₁(X) H₂(X), т.е. исход стрельбы по второй мишени обладает большей неопределенностью.