1.Канал без памяти

 канал связи, для к-рого статистич. свойства сигнала на выходе в момент времени tопределяются только сигналом на входе, переданном в этот момент времени t(и, следовательно, не зависят от сигналов, переданных до и после этого момента времени t).Точнее, канал связи с дискретным временем, сигналами на входе и выходе к-рого служат случайные последовательности h == (h₁, h₂, ...) и  =  с пространствами значений (Y, S_Y )и   соответственно, наз. К. б. п., если для любого натурального пи любых множеств   к=1,. . ., га, справедливо равенство

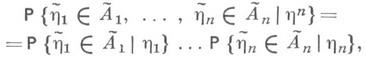
где hⁿ=(h₁:...,h_n). Если к тому же условные вероятности   не зависят от к, то К. б. п. наз. однородным.

Если обозначить через С _п канала пропускную способность отрезка длины поднородного К. б. п., то С _п=пС ₁. В случае, когда У и - конечные (или счетные) множества, однородный К. б. п. полностью задается матрицей переходных вероятностей     где

2.Классификация корректирующих кодов

Помехоустойчивые или корректирующие коды делятся на блочные и непрерывные. К блочнымотносятся коды, в которых каждому символу алфавита сообщений соответствует блок (кодовая комбинация) из n(i) элементов, где i - номер сообщения. Если n(i)=n, т.е. длина блока постоянна и не зависит от номера сообщения, то код называется равномерным. Такие коды чаще применяются на практике. Если длина блока зависит от номера сообщения, то блочный код называетсянеравномерным. В непрерывных кодах передаваемая информационная последовательность не разделяется на блоки, а проверочные элементы размещаются в определенном порядке между информационными. Проверочные элементы в отличие от информационных, относящихся к исходной последовательности, служат для обнаружения и исправления ошибок и формируются по определенным правилам.

Равномерные блочные коды делятся на разделимые и неразделимые. В разделимых кодах элементы разделяются на информационные и проверочные, занимающие определенные места в кодовой комбинации. В неразделимых кодах отсутствует деление элементов кодовых комбинаций на информационные и проверочные. Примером такого кода является семиэлементный телеграфный код №3 с весом каждой кодовой комбинации, равным трем. Этот код может служить только для обнаружения ошибок на основании изменения веса.

Разделимые коды делятся на систематические или линейные и несистематические или нелинейные. Линейные коды получили свое название потому, что их проверочные элементы представляют линейные комбинации информационных элементов. Большую и важную подгруппу линейных кодов образуют циклические коды. Линейные коды реализуются наиболее просто, что привело к их широкому использованию в УЗО. Для линейного кода применяется обозначение (n, k) - код, где n - число элементов в комбинации; k - число информационных элементов. Нелинейные коды характеризуются наличием двух или более систем проверок внутри каждой кодовой комбинации. Наиболее часто используются проверки на чётность числа единиц и нулей в разрешенных кодовых комбинациях.