3.2. Коэффициент наполнения

Коэффициент наполнения η_v равен отношению количества свежего заряда в цилиндре ДВС (G_1ц, кг или М_1ц, кмоль), поступившее за 1 цикл, к количеству заряда, которое размещается в объеме, равном объему цилиндра V_h при давлении р_к и температуре Т_к во впускном трубопроводе и может быть определен по формуле:

, (3.6)

где ρ_к, кг/м³ - плотность воздуха в заряде цилиндра.

Из уравнения Клапейрона для газа, находящегося в объеме цилиндра V_h, имеем . Тогда теоретическое количество свежего заряда G_1t, кг, которое могло бы быть в объеме V_h за один цикл можно определить по уравнению:

. (3.7)

Уравнение (3.3) в киломолях будет иметь вид: , из которого получим:

, (3.8)

где R_μ = 8,314 кДж/(кг∙К) – молярная (универсальная) газовая постоянная, а μ_в = 28,95 кг/кмоль – молярная масса воздуха.

Представление о теоретическом количестве заряда можно составить, если скорость поршня бесконечно мала, а цилиндр теплоизолирован (нет тепловых потерь). В этом случае давление и температура в цилиндре будут равны давлению и температуре во впускном коллекторе (р = р_к и Т = Т_к).

Коэффициент наполнения ДВС определяют, вычисляя количество теоретического заряда в цилиндре при атмосферном давлении и температуре р_о и Т_о на входе в ДВС, тогда формулу (3.2) можно записать в следующем виде:

. (3.9)

Масса действительного заряда обычно меньше теоретической, поскольку при впуске происходит нагрев заряда от стенок цилиндра и поршня, нагрев заряда от остаточных газов с температурой Т_r, занимающих, по меньшей мере, объем сжатия V_c и др., поэтому η_v < 1 (рис. 3.2).

Тем не менее, теоретически при наличии эффективной продувки или наддува может η_v > 1 при условии, что количество М_r остаточных от предыдущего цикла газов будет меньше объема сжатия V_c, а давление р в цилиндре в конце наполнения будет превышать давление р_к.

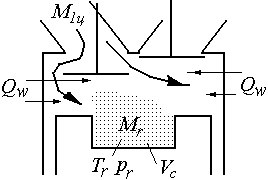
Рис. 3.2. Впуск свежего заряда в цилиндр ДВС:

T_r и p_r – температура и давление остаточных газов;

М_r и М_1ц – количество остаточных газов и свежего заряда

соответственно; Q_w – теплота, передающаяся заряду

от стенок цилиндра; V_c – объем камеры сгорания

3.3. Коэффициент остаточных газов

Рабочее тело в цилиндре в начале сжатия будет состоять из смеси М_1ц кмоль свежего заряда и М_r кмоль остаточных газов от предыдущего цикла:

М′_а = М_1ц+ М_r = М_1ц∙ ,

где коэффициент остаточных газов выражен уравнением:

. (3.10)

Поскольку закрытие впускного клапана происходит после Н.М.Т. (см. рис. 2.2), происходит дозарядка цилиндра и количество рабочего тела изменяется от М_а в начале до М_а′ в конце дозарядки, т.е. М_а′ = ξ_смМ_а, где ξ_см называют коэффициентом дозарядки.

Количество смеси газов в объеме V_a при положении поршня в Н.М.Т. определим из уравнения Клапейрона – Менделеева. Полагая, что параметры газов в цилиндре р_а и Т_а, получим: р_аV_a = M_aR_μТ_а и уравнение:

. (3.11)

Учитывая, что , и подставив (3.11) и (3.8) в (3.6), получим:

. (3.12)

В формулу (3.12) входят неизвестные величины: температура Т_а в конце наполнения цилиндра и коэффициент остаточных газов γ.

Рассматривая задачу о смешении газов при наполнении цилиндра свежим зарядом, определяют температуру газов в начале сжатия (Н.М.Т.), принимая допущения:

- продувка цилиндра не происходит;

- во впускном трубопроводе отсутствуют волновые явления и принимаем температуру, давление и энтальпию заторможенного потока постоянными: и ;

- давление газов в цилиндре во время наполнения не изменяется и равно давлению р_а.

Таким образом, рассмотрим задачу смешения газов в цилиндре с учетом теплообмена, но при постоянном давлении р_а.

В начале периода наполнения объем камеры сгорания V_c занимают остаточные газы от предыдущего цикла с параметрами р_r, T_r и удельной внутренней энергией u_r (рис. 3.2). Полная внутренняя энергия будет U_r = u_rG_r, где G_r - масса остаточных газов, которая не изменяется при наполнении цилиндра. Таким образом, смесь массой G_а в конце наполнения перемешана и состоит из массы G_r и массы G_1а свежего заряда и занимает объем V_а с параметрами р_а, Т_а и полной внутренней энергией U_а = u_aG_a.

Согласно первому закону термодинамики и с учетом принятых допущений запишем:

, (3.13)

где - работа газов при наполнении в цилиндре.

Поскольку i = u +pv из (3.13) получим:

. (3.14)

Если выразить количество газов в киломолях и учесть, что i = c_pT, получим: .

Пусть теплота Q_w подводится только к свежему заряду, и его температура повышается на ΔТ, тогда Q_w = ∙ ΔТ∙G_1а.

После подстановки значений в (3.14) получим:

, (3.15)

где - коэффициент дозарядки, который учитывает изменение количества кмоль свежего заряда за период дозарядки.

Уравнение (3.15) можно представить, заменяя массу в кг на кмоль, в следующем виде:

, (3.16)

где коэффициент учитывает изменение количества кмоль в смеси газов.

Разделим (3.16) на М_1ц и, учитывая (3.14), получим:

. (3.17)

Обозначая , деля (3.17) на и приняв , получим:

. (3.18)

При работе ДВС по внешней скоростной характеристике Т_r лежит в пределах 700 К для дизелей и 1100 К для ДВС с искровым зажиганием.

Применительно к четырехтактному ДВС уравнение (3.15) можно решить, если учесть, что остаточные газы в конце выпуска занимают объем камеры сгорания V_c при параметрах р_r и Т_r. Тогда, исходя из уравнения Клапейрона, получим:

, (3.19)

где R_п.с, Дж/(кг∙К) – газовая постоянная остаточных газов (продуктов сгорания).

По уравнению Клапейрона определим массу рабочей смеси в объеме V_a при параметрах р_а и Т_а:

. (3.20)

Из формулы (3.6) , поэтому, учитывая (3.7) в кг и (3.8) кмоль, получим:

или . (3.21)

Подставим (3.19), (3.20) и (3.21) в (3.15) и получим:

. (3.22)

Решая (3.22) относительно η_v, принимая во внимание, что и , обозначив и , получим:

. (3.23)

В формуле (3.23) при расчетах часто принимают ξ_с.з = ξ = 1,0, а ΔТ в пределах 0 – 20 К в четырехтактных ДВС с жидкостным охлаждением и 40 К в ДВС с воздушным охлаждением.

При испытаниях ДВС массу свежего заряда за 1 цикл определяют делением массового расхода воздуха G_к, измеряемого в кг/ч или кг/с на частоту циклов f_ц (с^-1 или мин^-1) и число цилиндров i ДВС: . Частота циклов равна частоте вращения коленчатого вала n в двухтактном ДВС (τ = 2) и в два раза меньше в четырехтактном ДВС (τ = 4), т.е.:

, c^-1. (3.24)

Тогда получим:

, кг/с. (3.25)

После подстановки (3.25) и (3.7) в (3.6) получим:

или . (3.26)

где G_в, кг/с – расход воздуха на входе в ДВС; V_h, м³ – рабочий объем цилиндра; ρ_о, кг/м³ – плотность воздуха на входе в ДВС.

Наиболее часто V_h обозначают в литрах (дм³), n – в мин^-1, а G_в – в кг/ч. Тогда расчет η_v проводят по формуле:

. (3.27)

При работе на полной нагрузке (номинальный режим):

- в дизелях η_v = 0,8 – 0,95;

- в ДВС с искровым зажиганием η_v = 0,7 – 0,85;

- в двухтактных ДВС η_v = 0,6 – 0,7.

В ДВС коэффициент наполнения определяется фазами газораспределения и его максимум соответствует частоте вращения вала ДВС n_м при максимальном моменте М_е (рис. 3.3).

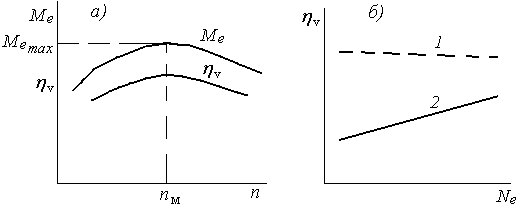
Рис. 3.3. Изменение η_v в поршневых двигателях:

а – в зависимости от частоты вращения n;

б – в зависимости от нагрузки N_e

─ ─ ─ ─ - дизель; ──── - бензиновый ДВС

При работе ДВС с искровым зажиганием на холостом ходу η_v ≈ 0,2 и при увеличении нагрузки (открытие дроссельной заслонки) η_v будет увеличиваться по зависимости близкой к линейной.

Если расход свежего заряда известен, то, измерив расход топлива G_Т (кг/ч), поступающий в цилиндры ДВС, можно определить средний по цилиндрам коэффициент избытка воздуха α в горючей смеси по формуле:

. (3.28)