Критический перепад давления

В минимальном сечении сопла устанавливается критическая скорость, вследствие чего это сечение и называется критическим сечением, а перепад давлений, при котором достигается критическая скорость называется критическим перепадом

.

В термодинамике критический перепал часто обозначается буквой .

Для определения численного значения критического перепада определим критическую скорость и скорость звука в критическом сечении и приравняем их величины.

По уравнениям термодинамики [1] для скорости звука в газе формула для адибатического процесса распростронения звука получена Лапласом

или

По Ньютону звуковые волны распространяются по изотермическому процессу и скорость звука равна , что на 18,5% меньше чем по Лапласу.

Из формул изменения состояния газа при политропных процессах из уравнения политропы p = pυⁿ и обозначения отношение давлений - в какой либо точке процесса к начальному давлению p₁ аналогично понятию степени расширения для такого же по характеру изменения давлений δ =

при R = const получим из уравнения политропы и уравнения состояниязависимость для определения T имеем T = T₁( = T₁δ . (13)

Для скорости звука в реагирующем газе из известной зависимости между давлением и плотностью в такой смеси или для скорости звука в реагирующей среде из уравнения Лапласа уравнения состояния или (14)

Из (14) с учётом (13) имеем

.

По формуле (12)

.

В соответствии с понятием критической скорости

,

т.е.

, (15)

откуда после сокращения на величину получим

или, после преобразований,

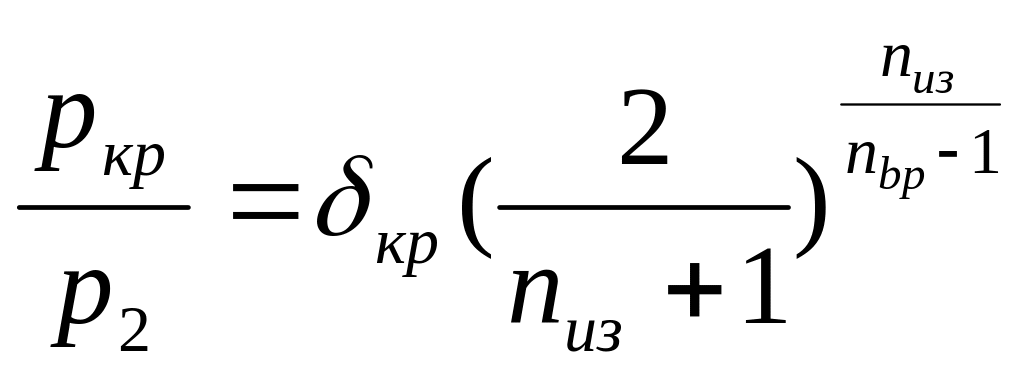(16)

Для адиабатического расширения химически инертного газа формула для критического перепада имеет вид

. (17)

Так, например, для воздуха при невысоких температурах и критический перепад давления равен

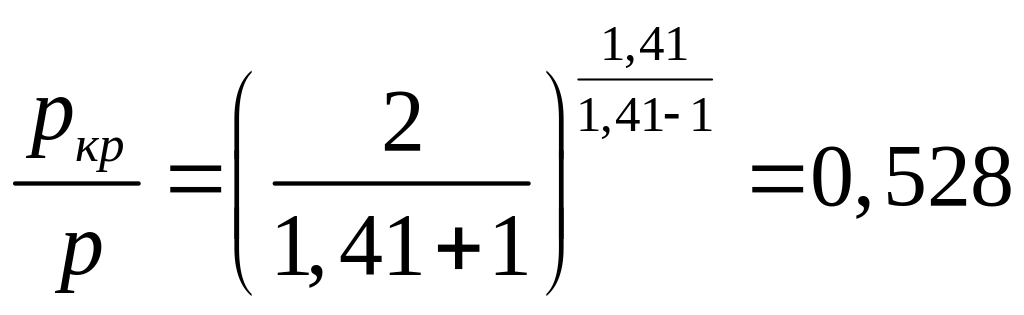
Следовательно, для воздуха давление в критическом сечении сопла

Изменение параметров газового потока по длине сопла

Для нахождения указанной зависимости запишем весовой расход через параметры критического сечения и любого другоо сечения f. и разделив первое на на второе получим подставив известные ρ_кр,ρ,ω_кр,, ω получим

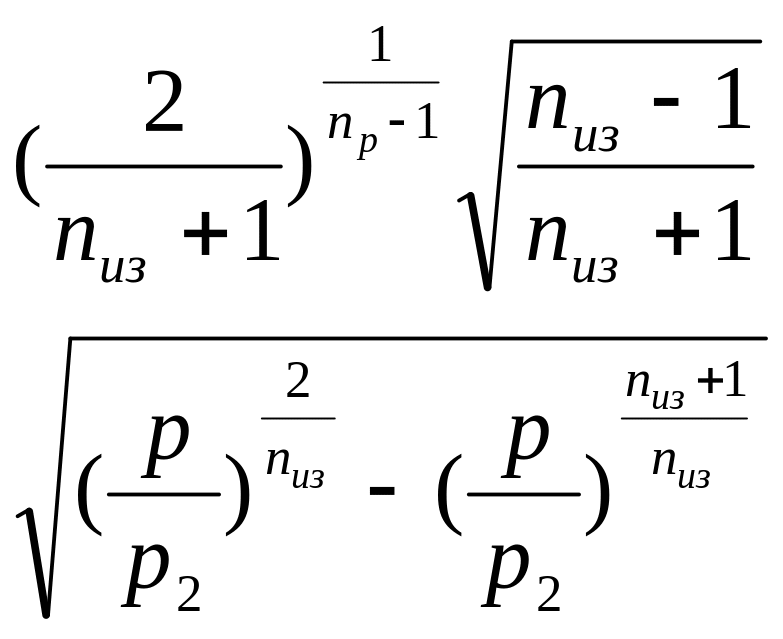= (18)

3.Теплосодержание топлива и продуктов сгорания

Физическое теплосодержание представляет собой количество тепла , которое затрачивается на нагрев данного (химически неизменного) вещества от абсолютного нуля 273,16⁰ до температуры T при которой оно используется в двигателе и будет выражаться

. Для жидких компонентов (весовой единицы ) величина физического теплосодержания будет равна I = c(T - T₀)

Тепловй эффект реакции горения называют также теплотой горения. Разница между величинами теплоты образования и химической энергией состоит в том, что при изменении вещества в процессе реакции происходит изменение запаса физического теплав нём. Это изменение физического тепла ∆Q = ,

где c_прод - теплоёмкость продуктов реакции (образования вещества)

с_исх - теплоёмкость исходных веществ.

Связь между теплотой образования и хим. энергией будет

∆H_T = I_хим + (с_прод - с_исх)T,

где (с_прод - с_исх)T = ∆Q - изменение запаса тепла, затраченного на изменение химической энергии I_хим, или

I_хим =∆H_T - (с_прод - с_исх)T При T =0 независимо от величины разности (с_прод - с_исх), ∆Q =0, а следовательно , I_хим = ∆H₀ (химическая энергия вещества равна его теплоте образования при абсолютном нуле)

Система отсчёта полных теплосодержаний .

Система отсчёта полных теплосодержаний различается по двум основным признакам:

1.Поинимается различная начальная температура отсчёта физических теплосодержаний T_0.

2. В разных системах условно химическую энергию относят к различным веществам (горючим, окислительным, образовавшимся.

Для уравнения оброзования воды будет:

H₂ + O₂ = H₂ O При этом выделяется энергия, равная - 57,8 ккал/г-моль . и полное уравнение образования воды будет:

H₂ + O₂ = H₂ O - 57,8 ккал/г моль.

Примем систему отсчёта теплосодержаний где:

1. Химическая энергия , выделяющаяся или затрачиваемая при протекании реакции относится к образовавшемуся веществу (например, к водороду, а для стандартных элементов она равна нулю)

2. Химичкская энергия вещества учитывается путём введения в полное теплосодержание величины его теплоты образования при 20⁰С, т.е.величины ∆H_293.16, или сокращённо ∆Н_293.

3. Химическая.энергия считается положительной, есл2и она затрачивается на образование вещества, и отрицательной ,если она этом выделяется.

4.За нуль отсчёта физических теплосодержаний принимается температура 20⁰С, т.е.293,16⁰абс.(или 293⁰абс.) Например, полное теплосодержание I_п для вещества с температурой T, будет I_п = ∆H _. + ( для жидких веществ I_п = ∆H _. + (T - 293) ).

Определение состава и температуры продуктов сгорания в камере сгорания (на входе в сопло ) и полного теплосодержания на срезе и теоретической скорости истечения.

C учётом эзоэнтропического расширения газа на срезе сопла S₂ =S₃ можно определить распределение давлении p_к и p₂ и показатель изоэнтропы из уравнения (16).

Из уравнения (2) имеем

ω₃ =91.5 где Δ I_п = - I

Для среза сопла удельный вес газа

γ₃ = . для 1 кг газа через выходное сечение 1 = f γ₃ ω₃ , где f -удельное проходное сечение на срезе сопла необходимое для пропускания 1кг газа в секунду, то есть f = или f = .

Зная f и ω₃ находим теоретическую удельную тягу по формуле (2а)

P_{уд.теор} = , по заданной абсолютной тяге P находим необходимый секундный расход топлива G_теор и теоретические размеры сопла на срезе

G_теор= (19)

f_{3 теор} = G f (20)

Для определения размеров критического сечения сопла из (16) необходимо знать показател изоэнтропы n_из. При этом вслучае высоких температурв камере сгорания и сильной диссоциации ,надо учитывать изменение газовой постоянной (или молекулярного веса ) продуктов сгорания в процессе расширения. С этой целью выведем уравнение изоэнтропического процесса в указанных условиях.

Уравнение изоэнтропы имеет вид pυ =const , заменив из уравнения состояния υ и применив уравнение точек 2 и 3 имеем

и логарифмируя находим с применением R =

n_из = (21)

Так как степень уширения сопла зависит от давлений на срезе, в камере и от показателя изоэнтропы, то вычислив n_из можно вычислить отношение проходных сечений , воспользовавшись формулой (18) и подставив в неё значения уширения δ = и величину n_из найдём fкр. теор.