2.3.2. Определение размеров камеры сгорания.

Наиболее распространённой формой К.С. является цилиндрическая. Объём камеры должен быть достаточным для возможно полного завершения процесса смесеобразования и сгорания компонентов топлива.

Для реализации процессов распыла, испарения, смешения и сгорания топлива необходимо определённое время, которое определяется размерами К.С.

Время пребывания должно быть равным времени необходимым для завершения элементарных процессов в К.С.

Для топлива НДМГ + АТ время пребывания в К.С. принимается равным .

Площадь и диаметр К.С. определяется на основе расходонапряжённости:

(2.38)

По экспериментальным данным:

, (2.38а)

тогда

и

Диаметр К.С. определяется по формуле:

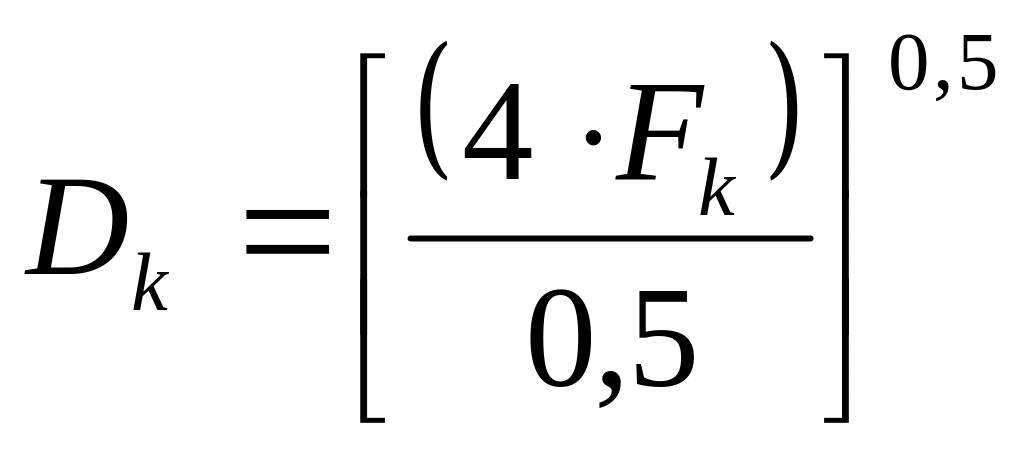, (2.39)

Длина цилиндрической части камеры равна:

(2.40)

где: - угол входа в сопло ,

(2.40а)

(2.40б)

Относительный диаметр цилиндрической части равен:

(2.40в)

Площадь критического сечения определяется:

(2.41)

отсюда диаметр критического сечения равен:

(2.41а)

Площадь выходного сечения сопла камеры определяется по степени расширения сопла .

, (2.42)

тогда диаметр выходного сечения сопла равен:

(2.42а)

2.3.3. Профилирование сверхзвуковой части сопла и выбор профиля для входной части.

Задача профилирования сопла состоит в том, чтобы определить такой контур стенок, при котором удовлетворялись бы следующие требования:

1) сопло должно иметь возможность меньше потерь тяги, т.е. возможно больше значение коэффициента сопла ;

2) поверхность стенок сопла при заданных и должно быть минимальной;

3) конструкция и технология изготовления сопла должны быть по возможности простыми.

Задача профилирования сопла, при котором газ разлагается до заданной скорости без образования скачков уплотнения, а движение потока направляется под определённым углом .

Исходные данные для расчёта сверхзвуковой части сопла приведены в табл. 2.5

Таблица 2.5

Параметры	Обозначение	Единицы измерения	Значения
Степень расширения газов		-	750
Диаметр критического сечения			0,1493
Диаметр среза сопла			1,2264
Показатель изонтропы истечения	æ	-	1,136
Показатель адиабаты		-	1,225

Профиль сопла проектируется таким образом, чтобы обеспечить максимальный КПД.

Расчёт и профилирование сопла производится по методике основанной на решении задачи по обтеканию идеальным газом угловой точки в критическом сечении сопла /10/.

Сопло профилируется промежуточной линией тока .

Безразмерная координата профиля равна:

(2.43)

Число Маха в исходном сечении определяется из соотношения:

(2.44)

Из работы по и находится , по величине которого определяется

(2.44)

Величину безразмерного расхода рассчитывают по формуле:

(2.45)

Из таблиц работы /10/ по и находят значения и .

Ближайшее табличное значение , соответствующее ему . Приняв их за окончательные значения для среза сопла получено:

,

отсюда

(2.46)

по табличному уточняется :

(2.46а)

Из таблиц работы /10/ выбираются значения и соответствующие им значения до , и по формулам (2.46) и (2.46а) определяют и . Результаты сводят в таблицу.

Входная дозвуковая часть сопла характеризуется плавными переходами, которые позволяют обеспечить минимальные потери и безотрывное течение газа в сужающемся сопле.

Геометрические обводы входной части приняты равными:

а) радиусу скругления при переходе цилиндрической части к выходной части сопла и ;

б) радиус очертания образующей входной части сопла в районе критического сечения и ;

в) угол конусности входной части и ;

г) длина входной части сопла определена исходя из геометрических очертаний и удобного сопряжения радиусов и .

Результаты расчётов по профилированию сопла приведены в табл. 2.6 и 2.7.

Расчётные данные сверхзвуковой части сопла.

Таблица 2.6

0,2206	0,9819	0,01771	0,157
0,2299	0,9868	0,01845	0,158
0,3443	1,048	0,02764	0,168
0,5512	1,165	0,04424	0,186
0,7554	1,284	0,06064	0,205
1,175	1,532	0,09432	0,245
1,506	1,725	0,12088	0,276
2,113	2,069	0,16961	0,331
2,738	2,403	0,21978	0,385
3,296	2,683	0,26457	0,429
3,742	2,895	0,30037	0,463
4,704	3,322	0,44461	0,532
5,539	3,662	0,55747	0,586
6,945	4,181	0,62361	0,669
7,769	4,457	0,76586	0,714
9,539	4,995	0,88055	0,8
10,97	5,381	1,08764	0,862
13,55	5,988	1,08764	0,959
15,78	6,437	1,26664	1,031
19,41	7,043	1,55802	1,128
22,68	7,482	1,82049	1,198

Геометрические размеры камеры

Таблица 2.7

Параметры	Обозначения	Единицы измерения	Значения
Площадь камеры			0,0524188
Площадь критического сечения			0,2583
Площадь на срезе сопла			1,18125
Диаметр камеры			0,0175
Диаметр критического сечения			0,1493
Диаметр среза сопла			1,2451
Длина камеры сгорания			0,3874
Длина входного сечения			0,0545
Длина сопла			1,8205
Длина цилиндрической части			0,3329
Полная длина камеры			2,2079

Энтропия и вероятностное состояния газов:

Велична , которая определяет изменение некоторой функции состояния газа есть энтропия, а T- температура при которой газ получает бесконечно малое количество тепла-dQ. В изолированной системе процесссы могут самопроизвольно протекать только так, что энтропия системы увеличивается или в пределе остаётся постоянной (2-ой закон термодинамики).

Вероятностным состоянием газа является изменение энтропии S₂ - S₁ = и чем более вероятно данное состояние газа тем больше величина энтропии.

Для вычисления энтропии газа или смеси газов применяются формулы

S_p = S₀ -AR ℓn p и = (8),

где М = -общее число граммолей газа в 1 кг смеси, S_pi - энтропия i-го газа , S₀ -энтропия индивидуального газа в кал/граммоль⁰С (задаётся в таблицах) и учитывая, что S_p = S₀ -AR lnp .( lnp = 2,303lgp), энтропия смеси = ккал/кг⁰С при температуре T и общем давлении p .

Источником энергии активации и энергии, необходимой для разложения продуктов сгорания , является энергия теплового дижения частиц ,составляющих газы. Количество частиц, обладающих данным запасом энергии, определяется с помощью

уравнения Максвелла:

N_i = A N₀ , (9)

где N_i - число всех частиц, имеющих запас энергии ε_i . N₀ -число всех частиц, k - постоянная Больцмана.

Элементарная теория сверхзвукового сопла

При ускорении газового потока вследствие расширения газа возможен переход скорости потока через скорость звука. Сопло, обеспечивающее получение сверхзвукового потока, называется сверхзвуковым соплом, или соплом Лаваля.

Если для ускорения потока несжимаемой жидкости в соответствии с формулой (III.2) необходимо все время уменьшать поперечное сечение потока, то в случае ускорения потока сжимаемого газа сопло получает более сложную форму.

Для определения формы сверхзвукового сопла исследуем уравнение закона сохранения массы (3), записав его для 1 кг газа в виде

, (10)

где - проходное сечение сопла, приходящееся на 1 кг газа.

Используя также соотношение , получим

, (11)

В сопле происходит процесс расширения, при котором изменяется как удельный объем , так и скорость газа .

Наиболее удобным параметром для расчета скорости и удельного объема является давление . При этом с уменьшением скорость газа увеличивается, а температура и скорость звука уменьшается; следовательно, при изменении в необходимых пределах скорость газа может стать выше критической (сверхзвуковой).

Рассмотрим далее изменение удельного объема и скорости в зависимости от отношения текущего давления к начальному давлению на входе в сопло, которое обозначим через . Выпишем соответствующие формулы

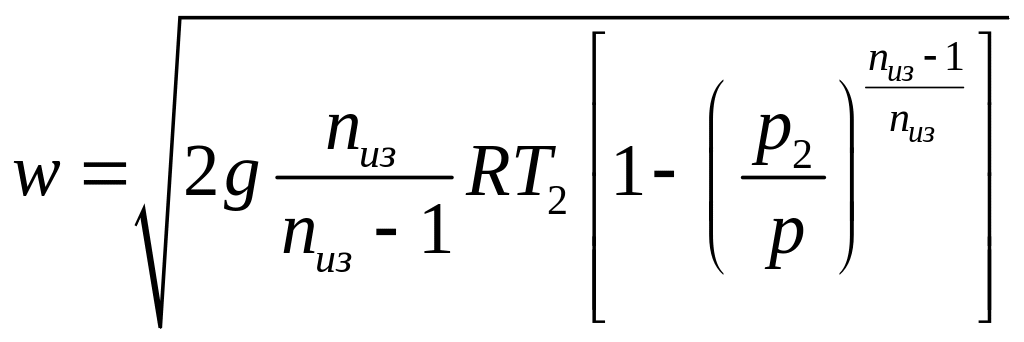(12)

и построим зависимость и от текущего давления .

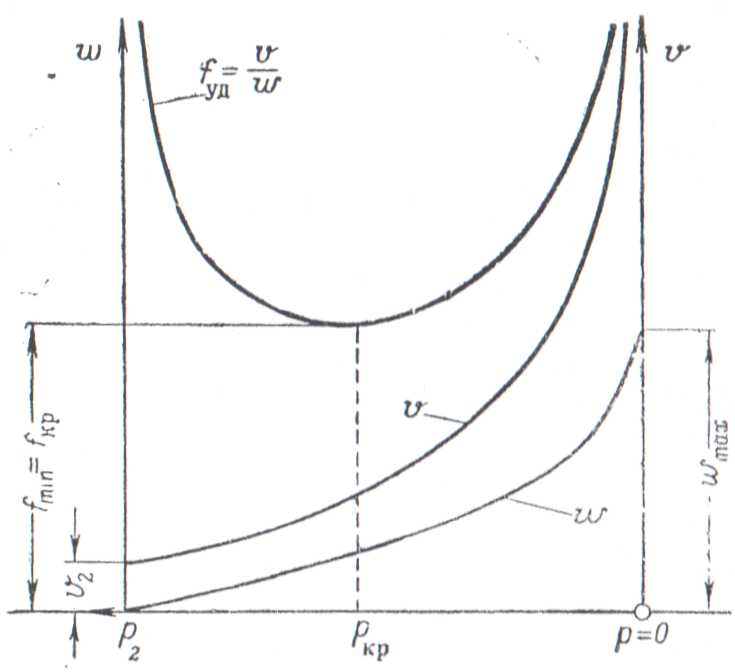
Удельный объем будет изменяться от начального удельного объема газа на выходе в сопло при давлении до удельного объема при давлении .

Скорость движения газа меняется от нуля при давлении (нет расширения) до максимальной скорости при , так как в последнем случае и .

Теперь нетрудно установить зависимость от давления , а следовательно, и от скорости .

При , т.е. ,

,

поэтому в соответствии с (11)

.

При т.е. удельный объем стремится к бесконечности, а скорость газа – к конечной величине , поэтому опять .

При р → 0, т.е. →0 удельный объём ₂стремится к бесконечности , а скорость газа - к конечной величине ω_max., поэтому опять f_уд → ∞.

При промежуточных значениях давления p лежащие между p =0 и p =p₂ величина удельного проходного сечения сопла f_уд имеет конечную величину и изменяется как показано на рис. fуд = . При давлении, равном p_к имеем минимальное значение необходимого проходного сечения f_уд.

В критическом сечении скорость звука и скорость движения газа равны, а поэтому сверхзвуковое сопло (сопло Лаваля) всегда имеет суживающуюся (докритическую) и расширяющуюся (закритическую) части Рис. 1