10.Вибрационная диагностика камеры сгорания.

Общие сведения.

10.1 Периодические функции.

Функция f(x) называется периодической, если существует постоянное число T>0, для которого

f(x + T) = f(x) (8.1)

каково бы не было x из области задания этой функции( Подразумевается, что в область задания вместе с x входят числа x + T и x_- T ) Число T с такими свойствами называется периодом функции f(x). Наиболее известными периодическими функциями являются

sin x . cos x.. tg x…Сумма, разность, произведение и частное функций периода Т очевид-но всегда дают функции того же периода.

Если T есть период функции f(x), то числа 2T, 3T,4T, . . будут также периодами, что сразу вытекает из рассмотрения графика периодической функции или из цепи равенств

f(x) = f(x + T) = f(x + 2T) = f(x + 3T) = …,

(наряду с этим равенством справедливы и такие f(x) = f(x - T) = f(x - 2T) = f(x - 3T) = …)

являющихся следствием многократного пользования условием (8.1).Таким образом, если T- период, то и всякое число вида kT, где k – положительное число, есть также период, т.е. период , если он существует, всегда не единственен. Отметим следующее свойство любой функции f(x) периода T.

Если f(x) интегрируема на некотором отрезке длины T, то она интегрируема на всяком другом отрезке той же длины, и величина интеграла при этом неизменна, т.е.

(8.2)

при любых a и b.

Это свойство легко вытекает из интерпретации интеграла, как площади рис 20.

Действительно, (так как по определению интеграла от функции f(x) он равен F(x) + C = , где F(x) есть первообразная функция производная или дифференциал от которой равен F΄(x) = f(x) или dF(x) = f(x) dx, а площадь под f(x) равна Ѕ(x)= F(x) ) интеграл (8.2) слагается из площадей, заключённых между кривой Y = f(x), крайними ординатами и осью Ox, причём площади, лежащие над осью Ox, берутся со знаком «+», а лежащие под осью Ox, со знаком «-».

В нашем случае в силу периодичности f(x) эти площади оказываются одинаковыми для обоих интегралов (8.2) рис 20.

Рис. 20

10.2 Гармоники.

Простейшей, и в то же время очень важной для приложений, является периодическая функция y= А sin( ωx + ), где А, ω, –постоянные. Эту функцию называют гармоникой с амплитудой IАI, частотой ω и начальной фазой . Гармоника имеет период Т=2 /ω. Действительно при любом x

А ѕin [ω ( x + )+ ] = А ѕin[( x + ) + 2 ] = А ѕin( x + )

Происхождение наименований « амплитуда », « частота », « начальная фаза » связано со следующей задачей механики о простейшем колебательном движении- гармонических колебаниях.

Пусть материальная точка М с массой m движется по прямой под действием силы F, пропорциональной расстоянию s точки М от фиксированной точки О рис21.

Рис.21

Считая, как обычно, s>0 справа от О и s<0 слева от О, т.е. задаваясь на прямой обычным положительным направлением, находим F=- ks, где k- коэффициент пропорциональности , k>0. По второму закону Ньютона произведение массы на её ускорение есть сила, которая действует на массу , а - y= А sin( ωx + )= s- путь массы . f^І(x) = y^І= А ω соs( ωx + )-первая производная или предел отношения приращения функции Δy = f( x +Δx) - f(x) к приращению аргумента Δx при Δx стремящемся к нулю( Δx 0). Отсюда видно, что, первая производная f^І(x) = y^І является скоростью- v массы- m, или скоростью колебаний. Вторая производная функции будет y^ІІ = d²s / dt²=d(А ω соs( ωx + ) ) = - Aω² sin( ωx + )= - ω²s – ускорением колебаний-J. Следовательно:

m d²s / dt² = - ks =F. или

m ω²s = ks. тогда

ω = - частота колебаний

Решением полученного дифференциального уравнения, как следует из сказанного выше является функция y= А sin( ωx + )= s, где А и - постоянные, которые можно вычислить, зная положение и скорость точки М в начальный момент, т.е. в момент t=0. Мы получили гармонику. Таким образом, s есть периодическая функция времени t с периодом T= 2 . Это означает, что под действием указанной силы F точка М будет совершать колебательное движение. Амплитуда - ІАІ есть максимальное отклонение точки М от О. Величина 1/Т есть число колебаний в единицу времени. Следовательно, 2 /Т есть число колебаний за отрезок времени длительностью в 2 единиц (секунд,

например). Отсюда наименование « частота». Величина - начальная фаза –характеризует положение точки М в начальный момент, так как при t=0 имеем : s₀ = sin .

Рассмотрим гармонику y= А sin( ωx + ). Её график при А=1, =1, =0 будет y= А sin x,

обычная синусоида рис 22,а

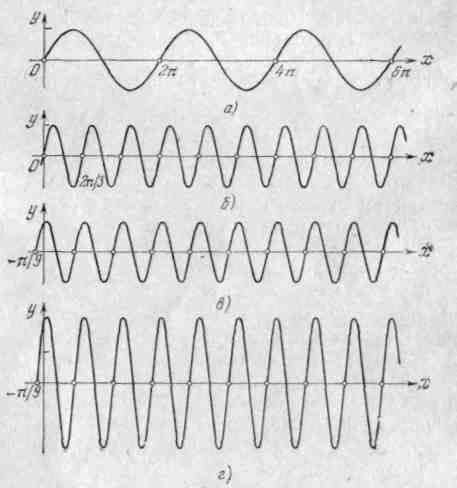
Рис 22

На рис 22 также изображены гармоники соответственно y= sin 3x с периодами 2 (рис.22б); y= sin (3x + с периодом Т=2 и начальной фазой (рис.22в). Наконец, графики гармоники y= А sin( ωx + ) получается из графика гармоники y= sin( ωx + ) умножением всех ординат на число А. На рис 22г изображена гармоника y= 2 sin(3x + То есть график всякой гармоники y= А sin( ωx + ) получается из обычной синусоиды равномерным сжатием или (растяжением) в направлении осей ординат.

Пользуясь известной формулой тригонометрии, напишем:

А sin( ωx + ) = А (cos х sin sin cоs .

Положив а =А sin b = А соs (8.3)

убедимся, что всякую гармонику можно представить в виде

a cos х + b sin (8.4)

и обратно, всякая функция вида (8.4) есть гармоника (чтобы убедится в этом, достаточно найти А и из уравнений (8.3). В дальнейшем для гармоники будем пользоваться записью вида (8.4). Для этого возьмём нестандартный период Т=2 и помня, что Т= 2 получим и, следовательно, гармоника с периодом Т = 2 может быть записана так:

а cos х + b sin х (8.5)

10.3 Тригонометрические многочлены и ряды.

Задаваясь числом Т= 2 и рассмотрим гармоники

а_κ cos k х/ + b_κ sin k х/ (k = 1,2, . . ) (8.6)

с частотами ω_к= k / и периодами Тк =2 _к = 2 /k.

Поскольку Т=2 = kТ_k, постольку число Т= 2 является периодом для всех гармоник (8.6) сразу (так как период, умноженный на целое число, опять даёт период-см. (8.1). Поэтому всякая сумма вида

s_n(х) = А + а_κ cos k х/ + b_κ sin k х/ ),

где А= соnst, будучи суммой функций периода 2 ,есть функция того же периода (прибавление постоянной, очевидно, не нарушает периодичности ; к тому же постоянную можно рассматривать как функцию, для которой любое число является периодом).

Функцию s_n(х) будем называть тригонометрическим многочленом порядка n (периода 2 ).

Тригонометрический многочлен хотя и слагается из нескольких гармоник, но представляет собой вообще функцию значительно более сложной природы, нежели простая гармоника. Располагая значениями постоянных А.а₁,b₁,а₂,b₂, . . .а_n,b_n, можно образовать функции y = s_n(х) с графиками, совсем непохожими на плавный и симметричный график простой гармоники. На рис.23 изображён график тригонометрического многочлена

Y = sin(х) + sin2х + sin3х.

Рис.23

Сумма бесконечного тригонометрического ряда

А + а_κ cos k х + b_κ sin k х)

(если он сходится) представляет собой также функцию периода 2 . Природа функций, являющихся суммами таких тригонометрических рядов, ещё более разнообразна.

Очень важено для приложений колебательных явлений то ,что всякую заданную функцию периода Т= 2 можно представить в виде суммы тригонометрического ряда для весьма широкого класса функций.

Пусть f(х) принадлежит этому классу. Это значит, что f(х) может быть разложена в сумму гармоник, т.е. в сумму функций очень простой структуры. График функций y = f(х) получается « наложением » графиков гармоник. Если трактовать каждую гармонику как простое гармоническое колебание, а f(х) как характеристику сложного колебательного движения, то последнее оказывается разложенным на сумму отдельных гармонических колебаний.

Если

f(х) = А + а_κ cos k х/ + b_κ sin k х/ ), (8.7)

то, положив =t или х =t / ,найдем для t) = f(t / ) периода 2

(х) = А + а_κ coskt + b_κ sinkt), (8.8)

Гармоники этого ряда имеют общий период 2 . Таким образом , если для f(х) нестандартного периода Т= 2 имеет место разложение (8.7),то для функции t) = f(t / ) периода Т= 2 .имеет место разложение (8.8). Справедливо и обратное заключение.

Таким образом, достаточно уметь решать задачу разложения в тригонометрический ряд для функций «стандартного» периода 2 .

10.4 Функциональные ряды. Интегрируемость и сходимость.

Если функция f(х) интегрируема на отрезке [а.b], то существует интеграл (хотя бы и несобственный)

в элементарном смысле. Таким образом, интегрируемая функция f(х) у нас всегда либо непрерывна, либо имеет на отрезке [а,b] конечное число точек разрыва, вблизи которых функция может быть как ограниченной, так и неограниченной. В интегральном исчислении [10] доказывается, что для функции с конечным числом точек разрыва из существования интеграла всегда следует существование интеграла

(обратное не всегда верно) при этом функцию f(х) называют абсолютно интегрируемой. Рассмотрим бесконечный функциональный ряд

f₁(х) + f₂(х) + . . . . f_k(х) +…… = f_k(x) (8.9)

Он называется сходящимся для данного значения х, если для его частных сумм

s_n(х) = f_k(x) (n =1,2,…)

существует конечный предел

s(х) = im s_n(х) при n→∞.

Величина s(х) называется тогда суммой ряда и, очевидно, представляет собой функцию от х. Если ряд сходится для всех х из отрезка [а.b], то то его сумма s(х) определена на [а.b].

Ряд (8.9) сходится равномерно на отрезке [а,b], если если для всякого положительного числа ε существует число Ν такое, что для всех n Ν и для всех x из из отрезка [а.b] выполняется неравенство

| S(х) - s_n(х)| ε

Если рассмотрим графики функций y = s (х) (сумма ряда) и y = s_n (х) (частная сумма ряда), то свойство равномерной сходимости означает, что для всех достаточно больших индексов n и для всех х графики суммы ряда и соответствующих его частных сумм отстоят друг от друга меньше чем на наперёд заданную величину- ε, т.е. эти графики равномерно (для всех х ) близки. В теории интегрального и дифференциального исчисления [10] доказано, что если члены ряда непрерывны на [а,b] и ряд сходится равномерно на этом отрезке, то сумма ряда s_n(х) есть функция непрерывная и ряд можно интегрировать почленно (те же свойства относятся и к почленному дифференцированию ряда)

Рассмотрим основную тригонометрическую систему, которой будем называть систему функций

1, соs х, sin х, соs 2х, sin 2х,… соs nх, sin nх…. (8.10)

Все эти функции имеют общий период 2 , а при любом целом n ≠ 0 при интегрировании получим:

cоs nх dх = 0; sin nх dх = 0; (8.11) и

cоs² nх dх =

(8.12)

sin² nх dх =

Пользуясь известными формулами тригонометрии для произведения синусов или косинусов разных углов имеем дл любых целых n и m

cоs nх cоs mх dх = 0; sin nх sin mх dх = 0; sin nх cоs mх dх = 0 (8.13)

Равенства (8.10)…(8.13) показывают, что интеграл от произведения двух любых различных функций системы (8.10) взятый по отрезку [- ] равен нулю.

Следовательно, если примем, что условием ортогональности двух функций на отрезке [а,b] будет ψ(х) (х) =о, то система (8.10) будет ортогональна на отрезке [- ] и на любом отрезке [ а, а + 2 ].

10.5 Ряд Фурье для функции периода Т=2 .

Пусть для функции f(х) периода 2 имеет место разложение .

f(х) = a₀/2 + а_κ cos k x + b_κ sin k х), (8.14)

Постоянное слагаемое здесь обозначено через a₀/2 для симметрии дальнейших формул.

Поставим себе задачу вычислить коэффициенты a₀, a_к, и b₀, b_к, к =1,2,…, зная функцию f(х).

Считаем, что для членов ряда выполнены условия § 8.4 о возможности почленного интегрирования ряда (8.14), функции f(х), а также рядов которые мы сейчас получим. Интегрируя равенство (8.14) в пределах от - до ,получим :

= a₀/2 + а_κ cos k x dх + b_κ sin k х dх ) (8.15)

В силу (8.11) все интегралы под знаком суммы равны нулю. Поэтому интегрируя первый член справа получи

a₀/2 = а₀/2 F(х)| = а₀/2 х| = a₀/2(π- (-π) )=πa₀ и (8.15) будет

= πa₀ (8.16)

Умножая обе части равенства ( 8.14) на cоs nх и результат опять интегрируем в прежних пределах. Получим:

f(x) sin nх dx = a₀/2 cоs nх dx + а_κ cоs nх cos k x + b_κ cоs nх sin k х)

В силу (8.11) первый интеграл справа равен нулю. Так как функции системы (8.10) попарно ортогональны, то все интегралы под знаком суммы, кроме одного, оказываются также равными нулю. Остаётся лишь интеграл

cоs² nх dx=

см. (8.12), являющийся коэффициентом при a_n. Таким образом, учитывая (8.16) имеем

f(x) cоs nх dx = a_{n (8.17)}

_{Аналогичным приёмом найдём, что}

f(x) sin nх dx = b_{n (8.18)}

_{Для коэффициентов Фурье имеем}

a_n = 1/ f(x) cоs nх dx и b_n = 1/ f(x) sin nх dx (8.19)

_{(n=0, 1, 2, . . . ) (n=0, 1, 2, . . .)}

_{Из (8.19) видно, что интегрируются функции периода 2 . Поэтому отрезок интегрирования [ - , ] может быть заменён любым другим отрезком длины 2 см.§ 8.1 и формулы для определения коэффициентов Фурье будут:}

a_n = 1/ f(x) cоs nх dx _{(n=0, 1, 2, . . . )}

_(8.20)

b_n = 1/ f(x) sin nх dx _{(n= 1, 2, . . . )}

Коэффициенты a_n b_n взятые по формулам (8.20) называются коэффициентами Фурье для функции f(х), а тригонометрический ряд

f(х) ≈ a₀/2 + а _n cos n x + b _n sin n х) _(8.21)

с такими коэффициентами называется её рядом Фурье при условии его сходимости и равенстве его суммы функции f(х).

10.5.1 В современной теории рядов Фурье [9] при услови интегрируемости и сходимости §9.4 приведены теоремы о замене функции f(х) рядом Фурь:

Теорема 1. Если для функции f(х) периода 2 имеет место разложение в некоторый равномерно сходящийся на всей оси о-х тригонометрический ряд, то этот ряд есть ряд Фурье для f(x).

Теорема 2. Если абсолютно интегрируемая функция f(х) периода 2 допускает разложение в некоторый тригонометрический ряд, сходящийся к ней всюду за исключением, быть может, конечного числа значений (для одного периода), то этот ряд есть ряд Фурье для f( х ) .

Соответственно для чётной f(х) = f(-х) и нечётной функций f(-х) = - f(х)

Коэффициенты Фурье для чётной и нечётной f(х) очевидны, если учесть интерпретацию интеграла как площади по которой для чётной и нечётной функции будет

= 2 _(8.22) -чётная и

= 0 (8.23) -нечётная, тогда

из (8.20) ,например, для нечётной функции и (8.22) и (8.23) будет

a_n = 1/ f(x) cоs nх dx = 0 _{(n=0, 1, 2, . . . )}

b_n = 1/ f(x) sin nх dx = 2/ f(x) sin nх dx (n=0, 1, 2, . .)

Следовательно, для нечётной функции ряд Фурье содержит лищь синусы,а для чётной косинусы:

f(х)≈ _(8.24)

f(х)≈ a₀/2 + а _n cos nx dx, а коэффициенты для чётной будут

b_n = 0, a_n = 2/ f(x) cоs nх dx

Основным свойством рядов Фурье является, то, что при приближённой замене функции f(х) тригонометрической суммой

s_n(х) = a₀/2 + a_nsin ωnх + b_n sin ωnх)

средняя квадратическая ошибка будет наименьшей, если за коэффициенты a_n и b_n взять коэффициенты Фурье данной функции.

δ²= 1/Т [ f(х)- s(х)]²dx

8.5.2 В дальнейшем при рассмотрении функции f(t), которую представляет вибрация, будем считать, что она соответствует функции f(х) из § 8.5.1 со свойствами (сходимость, интегрируемость и разложение в ряд). Докажем это на примерах колебаний различных простых систем и их сравнения с разложением Фурье функции колебаний.

11 Колебания простых механических систем и их функции. Источники вибрации механизма (тепловые и кинематические узлы). Узел вращения механизма. Вибрация, как функция источников и состояния силовой нагруженности узла.

11.1 Колебания простых механических систем и их функции.

Иллюстрацией механической системы колебаний является струна. Функция колебаний

Струны

Как показано в [10] амплитуда колебаний каждой точки струны рис. в этом случае будет y_n = Н_k·| sin k х |. При этом Н_k = . sin а_n = А_k/ Н_k , cоs а_n = В_k / Н_k , А_k, В_k- коэффициенты Фурье функции f(P) =y, а а_n=ω_n-собственные частота колебаний струны.

Точки для которых х = 0, /k, 2 /k, 3 /k , . . - это узлы пучностей стоячих волн( форм колебаний) струны с частотой основного тона ω₁ и частотами обертонов: 2ω₁ , 3ω₁. . . kω₁, . . . , тембром или окраской звука.

Как показано там же вынужденные колебания рассмотренной системы будут содержать собственные и вынужденные частоты и их гармоники.

В технике при создании и эксплуатации двигателя актуальной является задача виброзащиты при решении которой выделяют источник вибрации и объект виброзащиты [10].

В нашем случае при тех же общих задачах создания и эксплуатации двигателя для диагностики нагруженности и состояния его узлов привлекаются достижения математики, физики, электроники и особенно последней для использования теории колебаний при расшифровке вибраций, создаваемых механизмом, как функции его источника.

В рассматриваемом случае представляется удобным ввести понятия теплового и кинематического источников вибрации двигателя.

К тепловым источникам относятся узлы в которых тепло преобразуется в работу. Это в ГТД: камера сгорания, аппарат сопловых и рабочих лопаток турбины, реактивное сопло, в ДВС: цилиндр кривошипно-шатунного механизма, системы выхлопа и турбонаддува.

К кинематическим источникам вибрации двигателя относятся его узлы преобразующие работу в движение к которым относятся: валы, шестерни, воздушный винт, подшипники, колёса и другие.

Для иллюстрации приведённых понятий введём понятие «узел вращения», к которому будем относить все валы двигателя или механизма (с установленными на нем элементами), вращающиеся на своих опорах. На рис.24 показан элементарный «узел вращения»- вал на опорах с установленным на нём диском и приложенными к нему силами от дисбаланса диска.

Функция силы f(P) с которой диск действует на вал будет зависить его центробежной силы Р=ω²m(y+e), где e- эксцинтриситет (неуравновешенность) диска массой m и является прогибом вала y в центре О. Таким образом f(P)= ³/48ЕJ= y , где -длина вала, а –J момент инерции сечения вала.

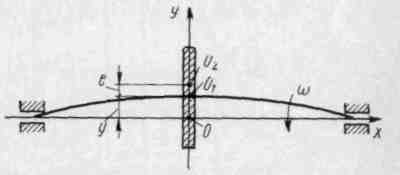
Рис.24

Элементарный узел вращения механизма.

Очевидно, так как вал рис.1 имеет симметричную нагрузку от неуравнове-шенности, то возмущающая сила при его вращения с угловой скоростью ω изменяется по закону функции вида :

f(t) =H sin(ωt +δ). (8.25)

Известно [2,3], что если возмущающая сила является функцией

f(t) =H sin(ωt +δ), которая является периодической с периодом Т= 2 ω, т.е. f(t +Т) = f(t), где H –амплитуда силы, ω –круговая частота возмущающей си-

лы, δ – начальная фаза и удовлетворяет условиям Дирихле (наличие на про- тяжении одного периода конечного числа максимумов и минимумов и конеч-

ного числа точек разрыва первого рода), то эту функцию можно разложить в ряд Фурье:

f(t) = А₀ + ( A_icos iωt + B_isin iωt ), где (8.26)

A_i = cos iωt dt , B_i = sin iωt dt (8.27)

В общем случае возмущающая сила злементарного узла вращения (рис.2) является функцией - f(t) =H sin(ωt +δ).

Примем для дальнейшего упрощения амплитуду и фазу возмущающей силы для элементарного узла вращения рис.24 H=1 и δ =0 имеем для неё из выражении (8.25) выражение f(t) = sin(ωt).

Тогда прогиб вала в направлении y (рис .24) по закону той же функции (8.25) имеет вид: f(y) = sin y.

Следовательно, вибрация опоры вала такого механизма(функция возмущающей силы), записанная в вертикальной плоскости по направлению y будет близка к виду:

f(y) = |sin y|, (8.28)

то – есть f(y) удовлетворяет условиям Дирихле и является непрерывной, кусочно -гладкой и чётной функцией.

Так как Іsin yІ = sin y , то для 0 ≤ y ≤ π первый член A₀ и последующие будут:

A₀ = sin y dy =

A_n = sin y cos ny dy = = - (8.29) если n ≠ 1.

Для n = 1, А₁ = sin y cos y dy = sin 2y dy = 0, В_n = 0 (n = 1,2,…..), так как f(y) чётна.

Таким образом функция перемещения вала элементарного узла рис.2 будет:

| sin y | = − ( + + + … ), то есть

| sin y | = − , где = − , а j =2,4,6,….n, или

| sin y | = f(t) =| sin ωt | = − ( + + + … ) (8.30)

ΙΙ.Алгоритм вибрационной диагностики «узла вращения» и выбор эталона.

Современный уровень развития электронной техники позволяет выделить из функции вибрации корпуса механизма по её разложению Фурье частоты гар-моник любого «узла вращения» механизма или всех валов- « узлов враще-ния»), а также частоты, возбуждаемые каким то процессом, например, про-цесссом горения в камере сгорания.

Диагностика состояния конкретного «узла вращения» основана на анализе вибрации, возбуждаемой этим «узлом вращения» по амплитудам ускорения его гармоник при испытаниях механизма на испытательном стенде или на обьекте на протяжении всего периода функционирования механизма.

Структурная схема алгоритма обработки функции вибрации узла механизма для определения его состояния и действующего крутящего момента ( для «узла вращения») на каком то определённом режиме работы (например, выбранных оборотах n_д ) изложена в [6,7] и состоит в следующем:

4.1 Место установки датчика на корпусе механизма(головка камеры сгорания).

Место установки выбирается по максимальному количеству частот гармоник вращения f₀ для выбранного для диагностики «узла вращения» ( f₀ –частота вращения, а -2 f₀ , 3 f₀. . . k f₀, . . . , гармоники частоты вращения).

. Анализ функции вибрации и диагностика по результатам анализа ведутся по параметру вибрации –ускорение силы тяжести - g м/сек² в диапазоне не ме-нее чем (f₀ . . .20f₀ ).

4.2. На оборотах- n_опт. и нагрузке- N_опт определяется сумма среднего уровня = амплитуд А_j всех гармоник частоты вращения в выбранном диапазоне частот измерения.

4. 3. Выделяются «информативные» гармоники за которые принимаются те из всех А_j, у которых амплитуды больше > (например,- А₂,А₃,А₅,А₁₁ )

4. 4. Определяется средняя сумма «информативных» гармоник ₌ (А₂+А₃+А₅+А₁₁) на оборотах п.4.2. структурной схемы алгоритма.

4. 5. На механизме с эталонным состоянием диагностируемого «узла вращения» определяется величина А = А_э и её вероятностные границы , которая является критерием его состояния. Диагностика осуществляется сравнением текущих значений А = А_т с эталонным значением А_э

Электронный блок диагностики и управления ресурсом рис.4 основан на программе, которая обрабатывает функцию вибрации с датчика, установленного на корпусе диагностируемого механизма, для заранее заданной частоты вращения «узла вращения» или всех «узлов вращения» и выполняет описанный алгоритм путём сравнения текущего значения А_т с эталонным - А_э .

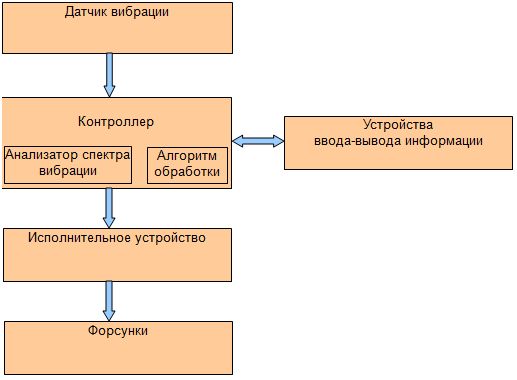
Рис.28

Управление работой механизмов, таких как двигатель внутреннего сгорания и кинема-тический механизм (редуктор), на основе анализа показаний различных датчиков, по программам работы различных систем двигателя, а также матрицы топливодозирования принципиально описано в [6]. .Применение приведенного алгоритма проверено на разных механизмах [7,8].

Приложение 1.

Соотношения между размерностями в различных системах измерения:

1. Сила

2. 1Н = 0.0981

3. Давление (жидкости, газа), механические напряжения:

1 атм = 1 кГ/см² = 735,6 мм Hg = 9,807*10⁴ Н/м².

1 Па (паскаль) = 1 Н/м²; 1 Мпа (мегапаскаль) = 10⁶ Па.

4. Температура:

Т К = 273,2 + t ⁰C.

5. Работа, энергия мощность:

1 кГм = 9,807 Дж

1 кВт час = 3,6 10⁶ Дж

1 л.с час = 2,648 10⁶ Дж

1 кВт час = 860 ккал

1 ккал = 426,09 кГм = 1,163 10^-3 кВт час

= 0,2043 Вт с

6. Коэффициент вязкости:

1 кг сек / м² = 98,1 г-масса / (см сек)

(дина см / сек² – пуаз)

1 пуаз = 100 сантипуаз = 0,0102 кг сек / м²

1 сантипуаз = 1,02 10^-4 кг сек / м² = 1,10^-3 кг / (сек м) = 3,6 кг / (час м)

7. Коэффициент кинематической вязкости:

1 м² / сек = 3600 м² / час = 10 000 см² / сек

1 см² / сек = 0,36 м² / час = 10^-1 м² / сек = 100 сст(сантистокс) =

= 14⁰УВ (градусов условной вязкости).

Литература

1. В.П. Бурдаков, Б.В. Дзюбенко, С.К.Михайлова. Термодинамика в 2 частях. Часть 1. Основной курс. Изд.: Дрофа,2009г.

В.П. Бурдаков, Б.В. Дзюбенко, С.К.Михайлова. Термодинамика в 2 частях. Часть 2. Специальный курс. Изд.: Дрофа,2009г.

2. М В. Добровольский, Жидкостные ракетные двигатели. – :Машиностроение.-2006, с.488

3 Г.Б. Синярёв, М.В.Добровольский Жидкостные ракетные двигатели. – :Машиностроение.-1957г и1968г , с.580.

4. В.Н.Луканин, М.Г. Шатров, Г.М. Камфер и др. Теплотехника. – М. : Высшая школа, 2000. -671с.: илл.

5 Р.А.Бережинский, В.Д.Горохов, В.А. Коробченко. Основы проектирование камер сгорания Ж Р Д: Учебное пособие/ Под общей ред. В.С. Рачука/ Воронеж: гос.техн.ун-т, 2004,с.129

6 Проблемы и перспективы развития двигателестроения :материалы докладов между-нар.. науч.-техн. конф. 24-26 июня 2009г. –Самара: СГАУ, 2009.- В 2Ч Ч.2. -220 с

7. Компьютерные технологии автоматизированного проектирования систем машиностро-ения и аэрокосмической техники: труды Российской конф. Воронеж: ГОУВПО «Воро-нежский государственный технический университет», 2008. 210 с.

8. . Ракетно- космическая техника и технология 2009; труды Росс. науч. - техн. конф., посвящённой 80 -летию со дня рождения главного конструктора, профессора В.П. Козелкова (1929-2002). Воронеж; ГОУВПО « Воронежский государственный технический университет», 2009. 229с.

9. Ракетно- космическая техника и технология…. 2010.

Тестовые вопросы по теплопередаче

№1

Назовите номера правильных ответов в порядке их задания:

Что является теплопроводностью, а что конвекцией:

1. Молекулярный перенос теплоты в среде с неоднородным распределением температуры посредством теплового движения макрочастиц.

2. Перенос теплоты с неоднородным распределением температуры при движении среды.

Что является теплоотдачей, а что теплопередачей?

3. Конвективный теплообмен между движущейся средой и поверхностью ее раздела с другой средой.

4. Процесс теплообмена между двумя теплоносителями.

Что является законом Фика?

5.

6.

№2

Назовите номера правильных ответов в порядке их задания:

Какой теплообмен является стационарным, нестационарным и стационарно-переодическим:

1. Температурное поле не зависит от времени.

2. Температурное поле зависит от времени.

3. Тепловые волны.

Какая формула определяет коэффициент диффузии для одного газа, а какая для смеси газов:

4.

5.

Что называется молекулярной, а что бинарной диффузией:

6. Перенос массы вещества

7. Перенос одного элемента вещества.

№3

Назовите номер правильного ответа в порядке их задания.

Что называется перепадом температур, а что градиентом:

1. разность между двумя точками одного тела

2. возрастание температуры по нормали к поверхности.

Что называется истнинным градиентом:

3.

4.

В каких пределах лежит(находится) коэффициент диффузии в твердых телах и жидкостях:

5. м²/с

6 м²/с

№4

Назовите номер правильного ответа в порядке их задания.

Что является истинным градиентом температуры:

1.

2.

Что является поверхностной плотностью теплового потока в единицу времени и вектором плотности теплового потока:

3. (Вт/м²)

4.

Что выражает тройную аналогию в газах и коэффициент теплопроводности:

5.

6.

№5

Назовите номер правильного ответа в порядке их задания.

Что является уравнением Био-Фурье и переноса теплоты:

1.

2.

Что отражает молекулярно-кинетическую теорию газов коэффициента теплопроводности:

3.

4.

Что является законом Ньютона при расчетах теплообмена между поверхностью и окружающей средой:

5.

6.

№ 6

Назовите номер правильного ответа в порядке их задания.

Что является уравнением переноса теплоты в скалярном виде и в виде закона Био - Фурье:

1.

2.

В каком порядке расположить значения коэффициентов теплопроводности для разных веществ.

3. газ

4. вода

5. металл

Что выражают коэффициенты массоотдачи и теплоотдачи в зависимости от толщины пограничного слоя и связь этих коэффициентов

4.

5.

6.

№7

Назовите номер правильного ответа в порядке их задания.

Какие значения имеет коэффициент теплопроводности для газов-водорода, азота и воды.

1.

2.

3.

Какой формулой определяется коэффициент теплопроводности при наличии слоя жидкости и газа конечной толщины и зависимость от температуры.

4.

5.

Назовите уравнения конвективного массообмена и переноса вещества термодиффузией.

6.

7.

№8

Назовите номер правильного ответа в порядке их задания.

Какие значения имеет коэффициент теплопроводности для теплоизоляционных материалов, для чистых металлов, для большинства металлов.

1.

2.

3.

Назовите уравнение с коэффициентом массоотдачи и аналогичное ему уравнение Ньютона для теплоотдачи

4.

5.

№9

Назовите номер правильного ответа в порядке их задания.

Какое уравнение определяет подъемную силу (Архимедову) в конвективном теплообмене, а какое связывает изменение плотности от перепада температуры:

1.

2.

Назовите уравнение коэффициента объемного расширения при конвективном теплообмене и уравнение Ньютона

3.

4.

Назовите уравнение диффузионного переноса теплоты и дифференциального уравнения диффузии.

5.

6.

№ 10

Назовите номер правильного ответа в порядке их задания.

Что позволяет рассматривать жидкости и газы как непрерывные и как разряженные среды с использованием статистических понятий для вынужденной конвекции:

1. Размеры области течения теплоносителей (жидкостей и газов) существенно превышает длину свободного пробега молекул, атомов.

2. Размеры области течения теплоносителей не превышают длину свободного пробега молекул.

Назовите уравнение термодиффузии и стационарной диффузии.

3.

4.

5.

№11

Назовите номер правильного ответа в порядке их задания.

Назовите уравнение переноса теплоты в движущейся среде при конвективном теплообмене, при чистом теплообмене, уравнение закона Ньютона, уравнение для определения коэффициента конвективной теплоотдачи:

1.

2.

3.

4

Какие соотношения для вязкой жидкости связывают динамическую вязкость с теплопроводностью и кинематическую вязкость:

5.

6.

№12

Назовите номер правильного ответа в порядке их задания.

Какой величиной является коэффициент конвективной теплоотдачи:

1. Физической характеристикой.

2. Функцией процесса в зависимости от

Каким уравнением определяется тепловой поток через поверхность А и через поверхность единичной площади:

3.

4.

Назовите уравнение, предложенное Ньютоном, для напряжения трения вязкой жидкости и уравнение Навье Стокса.

5.

6.

№13

Назовите номер правильного ответа в порядке их задания.

Что является средним градиентом температуры в пограничном слое , уравнением коэффициента теплоотдачи, вектором плотности теплового потока:

1.

2.

3.

4.

Назовите уравнение Навье Стокса в прямоугольных координатах через дивергенцию и при отсутствии сил давления и трения:

5.

6.

№14

Назовите номер правильного ответа в порядке их задания.

Что является законом Ома и Био-Фурье, какие уравнения описывают плотность потока теплоты и плотность тока:

1.

2.

3.

4.

Назовите напряжение сдвига (трения) жидкости у поверхности и коэффициент гидравлического сопротивления:

5.

6.

№15

Назовите номер правильного ответа в порядке их задания.

Назовите уравнение Максвелла для давления излучения, для давления газа на основе молекулярно-кинетической энергии, уравнение Эйнштейна для эквивалентности энергии и массы:

1.

2.

3.

Как связаны плотность излучения , поток излучения, проходящий через единицу поверхности и излучение . Какова скорость света и теплового излучения и сила давления света.

4. Па

5.

6. м/c

Какова скорость распространения электромагнитного излучения в веществе с коэффициентом преломления, и какой диапазон электромагнитного излучения обладает тепловым излучением:

7.

8.

№16

Назовите номера правильных ответов.

Что является критерием гидравлической монохромности и его физический смысл:

1.

2.

Что является критерием свободного движения среды и его физический смысл:

3.

4.

Что является конвекцией, а что теплопроводностью. Физика явления:

5. Молекулярный перенос теплоты в среде с неоднородным распределением температуры.

6. Перенос теплоты в среде с неоднородным распределением температуры при движении среды.

№17

Назовите номер правильного ответа в порядке их задания.

Что является критерием подобия (число Эйлера) и физический смысл:

1.

2.

Что является критерием полей свободного биения и физический смысл:

3.

4.

Что является средним градиентом, а что перепадом температур. Физика явления:

5.

6.

№18

Назовите номер правильного ответа в порядке их задания.

Что является формулой теплопроводности по Эйлеру, а что по Био-Фурье:

1. ;

2. ккал

Что является уравнением термодиффузии, а что стационарной диффузии:

3.

4.

5.

67