8.3. Метод описывающей функции. Асимптотические методы

План лекции

1. Метод описывающей функции

2. Асимптотические методы

Метод описывающей функции

Метод по существу является модификацией метода гармонического баланса для случая, когда систему мож­но разбить на линейную и нелинейную части, причем нелинейная часть такова, что ее свойства с удовлетво­ряющей нас точностью можно охарактеризовать, учиты­вая только одну гармонику.

При подаче на вход нелинейного элемента гармони­ческого колебания на выходе будет несколько гармоник, причем амплитуда и сдвиг фазы основной гармоники выходного сигнала зависят только от амплитуды вход­ной гармоники и не зависят от частоты.

Так, если acosrj)—входной сигнал, то амплитуда и фаза первой гармоники выходного сигнала могут быть выражены как функции амплитуды входного сигнала Ь(а)cos 6(a)].

Функции Ь (а) и 0 (а) называются описывающи­ми функциями, учитывающими в своем описании нелинейного элемента только первую гармонику выход­ного сигнала.

При таком рассмотрении нелинейный элемент может быть описан передаточной функцией

Если остальные элементы системы линейны и их ком­плексный коэффициент Передачи (ККП), (зависящий от частоты и не зависящий от амплитуды) /С_л(/(о), то си­стему можно разбить на две части: линейную и нели­нейную. Блок-схема такой системы изображена на рис. 10.6.

Автоколебания. В линейных системах при отсутствии внешних воздействий существует единственный стацио­нарный режим — статический, при котором все описы­вающие поведение системы величины постоянны.

В Нелинейных системах помимо статического может существовать автоколебательный стационарный

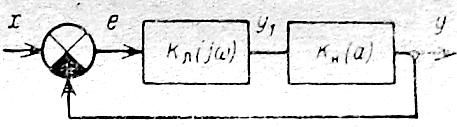
Рис. 8.5. Блок-схема системы с без­реактивным нелинейным элементом.

режим, при котором все описывающие поведение систе­мы величины — периодические функции вре- м е ни.

При существовании в системе автоколебаний их амплитуда и фаза находятся при х=0. Учитывая только первую гармонику автоколебаний, получим:

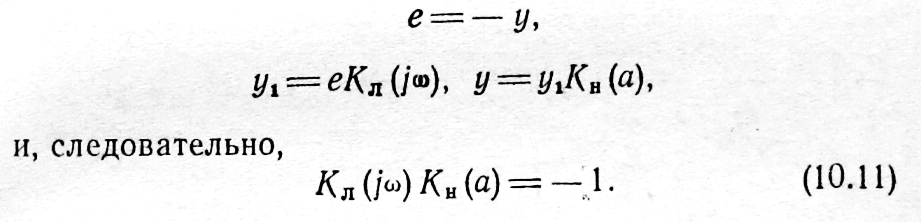8.11

Так как в общем случае —комплекс­ные величины, уравнение (10.10) распадается на два (действительная часть произведения при­равнивается к —1, а мнимая—к нулю), из которых в принципе можно определить амплитуду и частоту пер­вой гармоники автоколебаний.

Пример.RC-генератор синусоидальных колеба­ний (рис. 10.6). В шервом приближении нелинейную характери­стику лампы можно аппроксимировать полиномом третьей степени ц_а——ku_g+gu³_d-Еслиu_g=acosψто первая гармоника выходного напряжения определяется следующим соотношением.

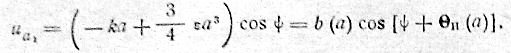
Из атого выражения следует, что передаточная функция не­линейного элемента равна

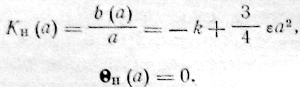
ККП линейной части трех /?С-цепочек, каждая с постоянной времениT—RC. определяется обычным методом и равна

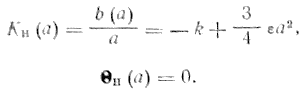
Для рассматриваемой схемы условие гармонического баланса соответствует уравнению . Знак плюс перед еди­ницей в правой части этого уравнения является результатом отсут­ствия в схеме вычитающего элемента.Подставив в это уравнение значенияКв[а) и Дл (/со), получим равенство

из которого определим частоту и амплитуду первой гармоники автоколебаний:

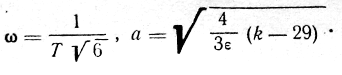
Последнее выражение позволяет определить условие возбуждения автоколебаний: k>29.

Асимптотические методы

Разработанные советскими учеными Крыловым Н. М., Боголюбовым Н. Н., Митропольским Ю. А. асимптотиче­ские методы являются комбинацией, дальнейшим углубленном н развитием методов возмущений и вариации параметров.

Решение в этих методах ищем в виде

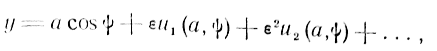
где — частота, равная резонансной частоте контура или мало отличающаяся от нее; а, -0-—ампли­туда и фаза колебаний — медленные функции времени.

Законы изменения амплитуды и фазы колебаний определяются уравнениями

Функции учитывают высшие гар­моники и не должны содержать основной частоты ω.

Зависимости определяются подстановкой в исходное дифференци­альное уравнение системы и приравниванием коэффици­ентов при одинаковых степенях в, как и в методе возму­щений. Более подробно с асимптотическими методами можно познакомиться в специальной литературе.

ЛЕКЦИЯ 26