Лекция 14
План лекции:
1. Рассказать о построении вещественной частотной характеристики.
2. Построение частотных характеристик замкнутых систем по передаточным функциям разомкнутой системы.
3. Рекомендуемая литература [1, 8 ].
5.3. Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам
РАЗОМКНУТОЙ СИСТЕМЫ
Вещественную частотную характеристику можно построить по АФЧХ, ЛАФЧХ замкнутой и разомкнутой системы. Рассмотрим построение вещественной частотной характеристики замкнутой системы по АФЧХ разомкнутой системы. Структурную схему системы можно представить в виде, показанном на рис. 5.3.
Используя зависимость между передаточными функциями замкнутой Ф(р) и разомкнутой W(p) системы, можно записать
(5.18)
Выделяя действительные и мнимые части функций Ф(р) и W(р), получим
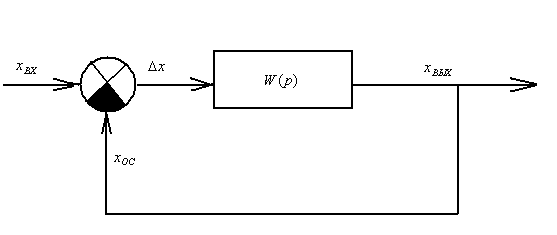
Рис. 5.3
Таким образом
(5.19)
(5.20)
Выражение (5.19) связывает вещественную частотную характеристику замкнутой системы U(ω) с вещественной Uр(ω) и мнимой Vр(ω) частями АФЧХ разомкнутой системы.
По формуле (5.19) построена номограмма (вещественная частотная диаграмма), которая позволяет определять ординаты вещественной частотной характеристики замкнутой системы по АФЧХ разомкнутой системы (рис. 5.4).
Номограмма представляет собой линии равных значений вещественной частотной характеристики, построенные в плоскости АФЧХ W(iω)=Uр(ω)+iVр(ω) разомкнутой системы.
Если при исследовании устойчивости использовались ЛАФЧХ, то для построения, вещественной характеристики можно воспользоваться аналогичными номограммами, приведенными в литературе.
5.4. ПОСТРОЕНИЕ АФЧХ ЗАМКНУТОЙ СИСТЕМЫ ПО ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТОЙ СИСТЕМЫ. ИСПОЛЬЗВАНИЕ АФЧХ ЗАМКНУТОЙ СИСТЕМЫ ДЛЯ ИССЛЕДОВАНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ И ПОСТРОЕНИЯ ВЕЩЕСТВЕННОЙ ХАРАКТЕРИСТИКИ.
При исследовании устойчивости САУ пользуются ЛЧХ разомкнутой системы. Расчет установившихся ошибок или исследование вынужденных колебаний при гармонических воздействиях производят с помощью ЛЧХ замкнутой системы. ЛЧХ замкнутой системы можно использовать также для построения вещественной частотной характеристики, по которой строится кривая переходного процесса. Это приводит к необходимости перехода от ЛАХ и ФЧХ разомкнутой системы к соответствующим характеристикам замкнутой системы.
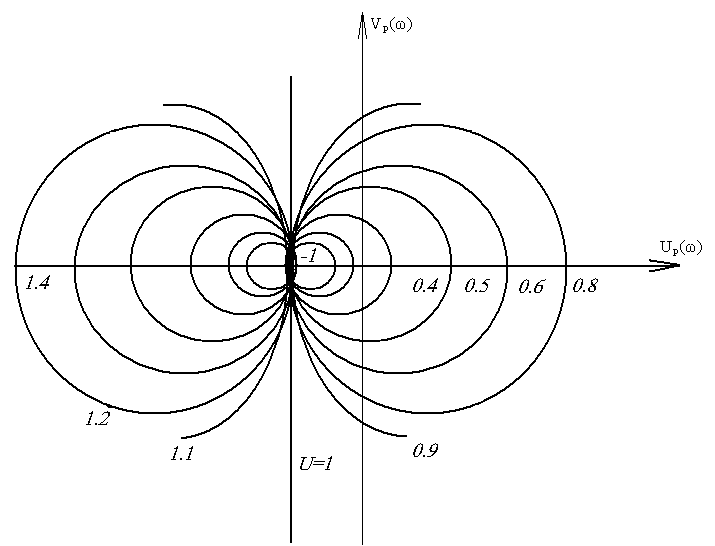
Рис. 5.4
Для этой цели можно воспользоваться номограммой замыкания, которая построена для единичной обратной связи (рис. 5.3).
Если система или местный замкнутый контур имеют неединичную обратную связь, то их структурные схемы необходимо преобразовать к виду, показанному на рис. 5.5.
В основу построения номограммы для замыкания системы положена формула (5.18).
АФЧХ замкнутой и разомкнутой системы можно представить в следующем виде:
(5.21)
(5.22)
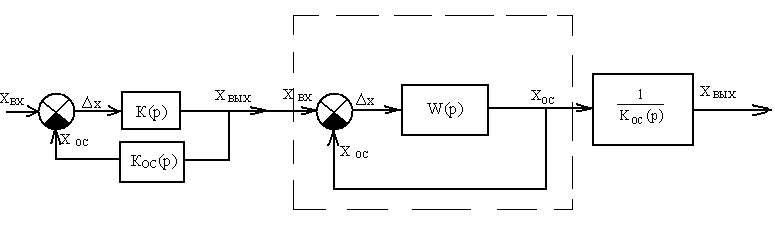
Рис. 5.5
Подставляя формулы (5.21) и (5.22) в выражение (5.18), получим
или
(5.23)
Разложив 
по формуле Эйлера, выражение (5.23) перепишем
в виде
Приравнивая мнимые и действительные части полученного выражения, можно записать:
Мсоs(ψ – φ)+МНсоsψ =Н; (5.24) sin(ψ – φ)+Hsinψ = 0 . (5.25)
Уравнения (5.24) и (5.25), предварительно записанные в логарифмическом масштабе, позволяют построить в плоскости НдБ , φ° линии равных значений МдБ и ψ°. Совокупность линий МдБ и ψ°, построенных в плоскости НдБ , φ° называется номограммой замыкания системы (рис.5.6).
Чтобы найти ординаты логарифмической амплитудной Мдб и фазовой ψ° характеристик функции Ф(iω) при некотором фиксированном значении частоты ω1, надо для разомкнутой системы определить значения Н(ω1)дБ и φ°(ω1) и отложить их по осям номограммы.
Проводя через точки Н(ω1)дБ и φ°(ω1) соответственно горизонталь и вертикаль, получим точку их пересечения в плоскости номограммы. Кривые МдБ и ψ°, проходящие через эту точку, равны соответственно значениям ординат ЛАЧХ и ЛФЧХ замкнутой системы при частоте ω1. Аналогично определяются МдБ и ψ° при других фиксированных значениях частоты и получаются таким образом зависимости МдБ (ω) и ψ°(ω). Процесс замыкания можно существенно упростить, если воспользоваться следующими рекомендациями.
При
Н
>>1 в выражении
единицей в знаменателе можно
пренебречь,
тогда Ф(iω)
≈ 1,
т.е.
МдБ ≈ 0 и ψ° ≈ 0 .
Учитывая это, приходим к выводу, что продолжать номограмму вверх за значения НдБ =25 ÷ 30 дБ не имеет смысла, т.к. для значений НдБ > 25 дБ можно считать, что МдБ = 0 и ψ° = 0.
При H<<1 будем иметь Ф(iω) ≈ W(iω), т.е. при больших по абсолютному значению отрицательных НдБ частотные характеристики разомкнутой и замкнутой систем совпадают, поэтому продолжать номограмму вниз за значение - (25÷30) дБ также не имеет смысла, т.к. для значений НдБ < – 25дБ МдБ ≈НдБ , а ψ° ≈ φ°.
Представленные на номограмме кривые симметричны относительно вертикальной оси, проходящей через точку с координатой φ°= – 180°, причем индексы симметричных половин кривых МдБ совпадают как по величине, так и по знаку, а индексы симметричных кривых ψ°, будучи одинаковыми по величине, различаются знаком (например, кривой с индексом ψ° = – 60° соответствует в левой половине номограммы симметричная кривая с индексом ψ° = 60° = – 300°). В силу этой симметрии полную номограмму можно заменить ее половиной, соответствующей значениям φ° от 0 до –180°. Для удобства некоторые номограммы снабжены шкалой φ° с двойной индексацией.
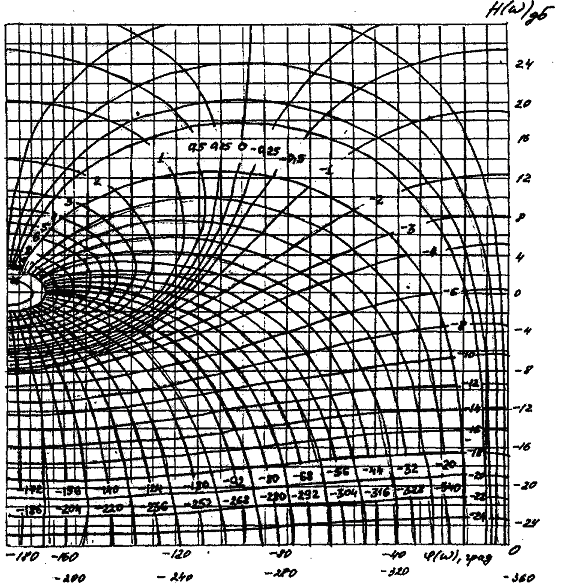
Рис.5.6
Номограмма может быть применена для построения характеристик передаточной функции по ошибке
Для этого достаточно иметь в виду следующую зависимость:
Действительная часть АФЧХ замкнутой системы (вещественная частотная характеристика) U(ω) связана с модулем (АЧХ) М(ω) и аргументом (ФЧХ) ψ°(ω) замкнутой системы следующим выражением:
(5.26)
Таким образом, имея ЛАФЧХ замкнутой системы, можно легко построить вещественную характеристику. Для этого достаточно перейти от логарифмического масштаба МдБ (ω)=20lgМ(ω) к обычному М(ω) и воспользоваться формулой (5.26).
Характеристику М(ω) используют для анализа вынужденных колебаний САУ при гармоническом внешнем воздействии.
В самом деле, АЧХ замкнутой системы
,
т.е.
,
(5.27)
где
- амплитуда выходной величины;
-
амплитуда входной величины;
ωк - фиксированное значение частоты воздействия.
Таким
образом, если
=
sin
ωt,
то
=
sin(ωt+
ψ°
),
где
определяется
по выражению (5.27), а ψ°
–
по ФЧХ замкнутой системы.
ЛЕКЦИЯ 15