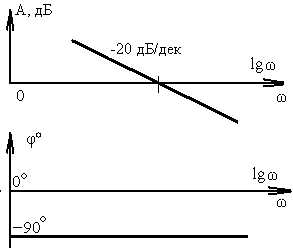- •Родионов в.И.
- •Конспект лекций
- •«Теория автоматического управления»
- •Содержание
- •Основные понятия и определения тау
- •Функциональные элементы сау
- •Классификация систем автоматического
- •1.3. Примеры систем автоматического управления
- •2. Математическое описание сау
- •Виды воздействий. Управляющие и возмущающие воздействия.
- •Вынужденное движение и собственные колебания системы.
- •2.1. Виды воздействий. Управляющие и возмущающие воздействия
- •Вынужденное движение и собственные колебания системы. Переходный и установившийся режимы
- •2.3. Передаточные функции
- •2.4. Переходная характеристика и весовая функция
- •Типовые звенья систем автоматического
- •2.6. Неустойчивые и неминимально–фазовые звенья
- •2.7. Структурные схемы сау
- •2.8. Составление и преобразование структурных схем сау
- •2.9. Передаточные функции замкнутой и разомкнутой
- •Установившиеся режимы
- •3.1. Точность сау в установившемся режиме
- •3.2. Установившиеся ошибки следящих систем
- •Частотные характеристики сау
- •Логарифмические амплитуднные и фазовые
- •3.5. Частотные характеристики типовых звеньев
- •3.6. Особенности частотных характеристик устойчивых
- •4. Устойчивость систем автоматического управления
- •4.1. Общие понятия об устойчивости заданного режима
- •4.2. Определение устойчивости по а.М. Ляпунову
- •3. Критерий устойчивости гурвица
- •Таким образом, кроме положительности коэффициентов а30; а20; а10; а00
- •4.4. Критерий михайлова
- •4.5. Критерий найквиста
- •4.6. Суждение об устойчивости по лафчх
- •4.7. Выделение областей устойчивости
- •Суждение об устойчивости системы
- •5. Качество сау
- •5.1. Основные показатели качества
- •5.2. Методы построения переходных процессов
- •Преобразования Фурье имеют вид:
- •5.2.1 . Частотный метод анализа качества сау,
- •Приближенный метод построения кривой переходного процесса с помощью трапециидальных частотных
- •Лекция 14
- •5.3. Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам
- •План лекции:
- •5.5. Косвенные оценки качества, связанные с распределением нулей и полюсов передаточной функции
- •5.7. Интегральные оценки качества
- •5.8. Косвенные оценки качества, связанные с видом
- •5.8.1. Анализ качества по ачх замкнутой системы
- •5.8.2. Оценка качества сау по логарифмическим частотным
- •Приближенная оценка вида переходного процесса
- •6. Динамический синтез сау
- •6.1. Общие понятия синтеза сау
- •6.2. Этапы синтеза сау
- •6.3. Требования, предъявляемые к динамическим
- •Методы коррекции динамических свойств сау.
- •5. Методы коррекции динамических свойств системы,
- •6.5. Динамический синтез сау, основанный
- •6.6. Синтез последовательного корректирующего устройства
- •6.7. Синтез параллельного корректирующего устройства
- •7. Методы синтеза, основанные на теории
- •7.1. Уравнения системы в пространстве состояний
- •7.2. Коррекция системы в пространстве состояний
- •7.3. Прямой корневой метод синтеза
- •7.4. Прямой корневой метод синтеза сау по координатам пространства состояний
- •8. Нелинейные системы автоматического управления. Аналитические методы исследования Лекция 22
- •8.1Метод возмущений (метод малого параметра).
- •8.2Метод возмущений (метод малого параметра)
- •8.2. Методы минимизации невязки. Метод гармонического баланса
- •Методы минимизации невязки
- •Метод гармонического баланса
- •8.3. Метод описывающей функции. Асимптотические методы
- •8.4. Метод припасовывания.
- •8.5. Метод точечного преобразования.
- •8.6. Примеры точечного преобразования.
- •8.7. Исходные положения метода гармонической линеаризации.
- •8.7. Частотный способ определения симметричных автоколебаний.
- •9.. Прохождение случайных воздействий
- •9.1. Интегральное Уравнение связи
- •9.2. Спектральное уравнение связи
- •9.3. Определение динамических характеристик сау
- •9.4. Методы определения ошибок линейных сау,
- •9.5. Эквивалентное представление стационарного
- •9.6. Расчет флуктуационных ошибок и ошибок
- •9.7. Расчет дисперсии помехи с помощью корреляционной функции. Вычисление среднеквадратической ошибки следящей системы
- •9.8. Расчет дисперсии помехи с помощью
- •9.9 Вычисление среднеквадратической ошибки
3.5. Частотные характеристики типовых звеньев
Выше было отмечено, что ЛАФЧХ любой, как угодно сложной САУ, можно построить практически без расчетов по известным ЛАФЧХ типовых звеньев, которые сведены в табл. 3.1.
1.
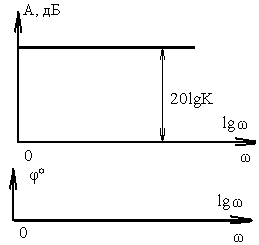
Усилительное звено. Передаточная
функция этого звена
![]() .
Амплитудно-фазовая частотная характеристика
имеет вид
.
Амплитудно-фазовая частотная характеристика
имеет вид
![]() .
(3.31)
.
(3.31)
Согласно (3.24), (3.25) и (3.31) имеем:
![]() .
(3.32)
.
(3.32)
Логарифмическая амплитудная частотная характеристика
![]() .
(3.33)
.
(3.33)
Анализ (3.32) и (3.33) показывает, что ЛАХ усилительного звена не зависит от частоты, а ФЧХ равна 0.
2. Интегрирующее
звено.
Передаточная функция этого звена имеет
вид
![]() АФЧХ равна
АФЧХ равна
![]() .
(3.34)
.
(3.34)
Согласно (3.34) имеем:
![]() .
(3.35)
.
(3.35)
На основании (3.35)
![]() .
(3.36)
.
(3.36)
ЛАХ
пересекает ось частот при
![]() т.е.
т.е.
![]() ,
или
,
или
![]() . (3.37)
. (3.37)
Найдем изменение ЛАХ (по амплитуде) при изменении частоты на одну декаду
![]() .(3.38)
.(3.38)
Таким
образом, ЛАХ интегрирующего звена
согласно (3.36), (3.37) и (3.38) представляет
собой прямую линию с наклоном (-20) дБ/дек,
пересекающую ось частот при
![]() .
.
3. Апериодическое (инерционное) звено. Передаточная функция этого звена имеет вид
![]()
АФЧХ равна
![]() (3.39)
(3.39)
где
![]() ;
;
![]()
Согласно (3.39) АЧХ и ФЧХ имеют вид:
![]()
![]() .
(3.40)
.
(3.40)
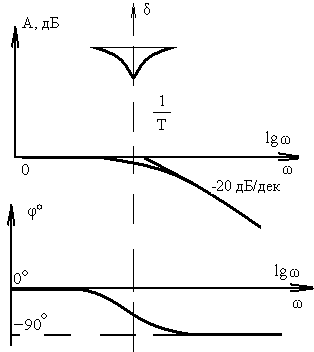
ЛАЧХ апериодического звена
![]() (3.41)
(3.41)
может быть приближенно представлена ломаной линией. Эта приближенная характеристика называется асимптотической ЛАЧХ. Такое название связано с тем, что эта характеристика построена из двух асимптот, к которым стремится ЛАЧХ при 0 и . Найдем эти асимптоты.
При малых значениях 1/T в выражении (3.41)
![]() т.е.
т.е.
![]()
В этом случае характеристика представляет собой прямую, параллельную оси частот и проходящую на уровне 20 lg k. Это есть низкочастотная асимптота, к которой стремится ЛАЧХ при 0.
С другой стороны, на больших частотах, когда >> 1/T имеем
![]() ,
т. е.
,
т. е.
![]() .
.
В этом случае характеристика представляет собой прямую, имеющую наклон (-20) дБ/дек. Действительно, при увеличении на 1 декаду, т.е. в 10 раз
![]()
![]()
Эта линия является высокочастотной асимптотой, к которой стремится ЛАЧХ при . Обе асимптоты пересекаются на сопрягающей частоте 1/T.
При 1/T согласно (3.41) имеем
![]() .
.
Таким образом, максимальное расхождение между истинной и асимптотической ЛАЧХ равно всего 3 дБ. Поэтому при практических построениях используют обычно асимптотическую ЛАЧХ.
Фазовая частотная характеристика, соответствующая выражению (3.40), при изменяется от 0 до (–). При этом в точке 1/T фазовая характеристика ( ) .
Если частотные характеристики получены экспериментально, по ним нетрудно определить параметры звена Т и k, пользуясь описанной выше зависимостью между этими характеристиками и передаточной функцией.
4. Колебательное звено. Передаточная функция колебательного звена имеет вид
![]() .
(3.42)
.
(3.42)
АФЧХ
![]() ,
согласно (3.42), равна
,
согласно (3.42), равна
![]() .
(3.43)
.
(3.43)
Исходя из выражения (3.43) получим:
![]() ;
(3.44)
;
(3.44)
![]() .
(3.45)
.
(3.45)
На основании (3.44) можно записать
![]() .
(3.46)
.
(3.46)
Тогда ЛАЧХ можно представить в виде двух асимптот, к которым она стремится при 0 и .
Уравнение низкочастотной асимптоты получается из (3.46) при 1/T
![]() .
.
Уравнение высокочастотной асимптоты при 0 имеет вид
![]() .
(3.47)
.
(3.47)
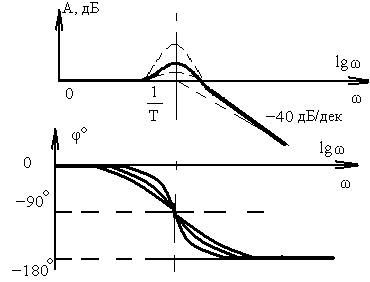
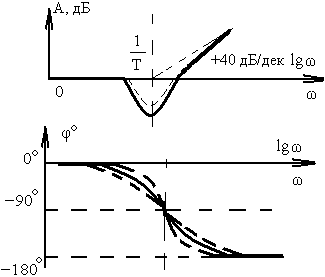
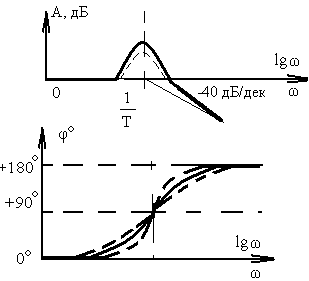
Из последнего выражения следует, что при увеличении частоты на 1 декаду ЛАЧХ понижается на 40 дБ, что и определяет наклон высокочастотной асимптоты в (- 40) дБ/дек. В области средних частот ( 1/T) асимптотическую ЛАЧХ корректируют с помощью готовых графиков поправок, дающих разность между истинной к асимптотической ЛАЧХ. Графики поправок (рис.3.3.) и фазовые частотные характеристики колебательного звена (рис.3.3.) существенно зависят от величины .
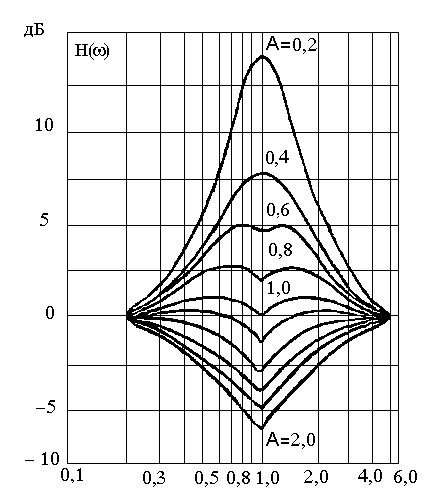
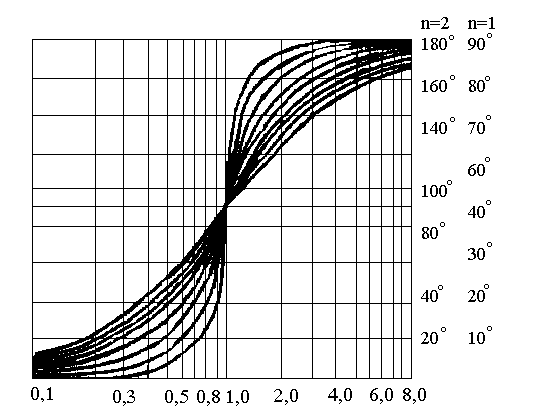
Рис.3.3
Таблица 3.1
№ п/п |
Типовое звено |
Передаточная функция |
ЛАФЧХ |
1 |
2 |
3 |
4 |
1 |
Усилительное |
k |
|
2 |
Дифференцирующее |
Tp |
|
3 |
Интегрирующее |
1 / Tp |
|
4 |
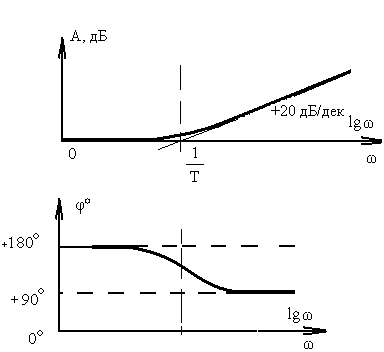
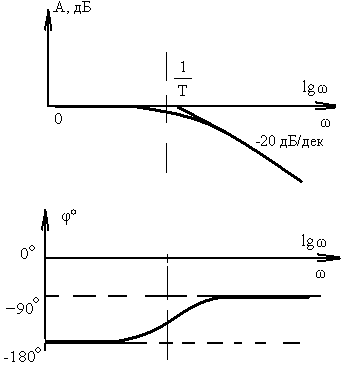
Апериодическое |
1 / (Tp+1) |
|
5 |
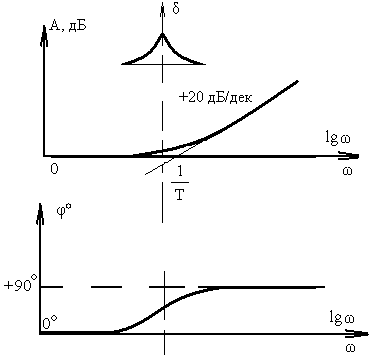
Форсирующее первого порядка |
Tp+1 |
|
6 |
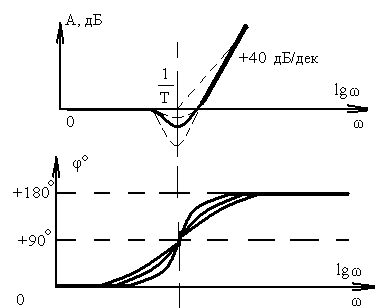
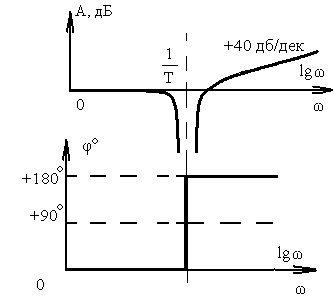
Форсирующее второго порядка |
|
|
7 |
Колебательное |
|
|
8 |
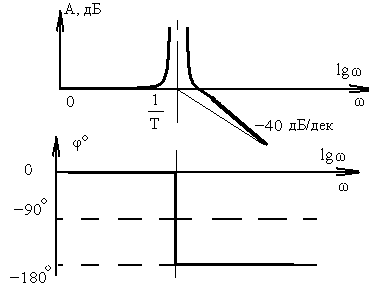
Колебательное
при
(демпфирование отсутствует) |
|
|
9 |
Форсирующее звено второго порядка при
|
|
|
10 |
Неустойчивое форсирующее звено первого порядка |
Tp-1 |
|
11 |
Неустойчивое форсирующее звено второго порядка |
|
|
12 |
Неустойчивое апериодическое |
|
|
13 |
Фазоинверсное |
- 1 |
|
14 |
Неустойчивое колебательное |
|
|
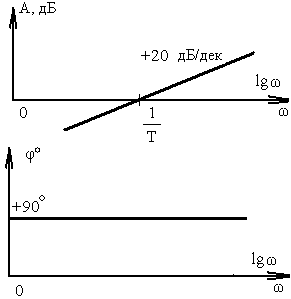
5. Дифференцирующее и форсирующее звенья. ЛАФЧХ дифференцирующего и форсирующих (первого и второго порядка) звеньев можно получить зеркальным отражением относительно оси частот соответственно интегрирующего, апериодического и колебательного звеньев.