3.8.3. Меры связности графа. Вершинная и реберная связность

Определение. Вершинной связностью графа G называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу.

Примеры.

=0, если граф G несвязен; =1, если граф G имеет точку сочленения;

, если (G – полный граф с p вершинами).

Определение. Если , то граф G называют k-связным.

На рис. 3 приведен пример 2-связного графа.

Рис. 3

Определение. Реберной связностью 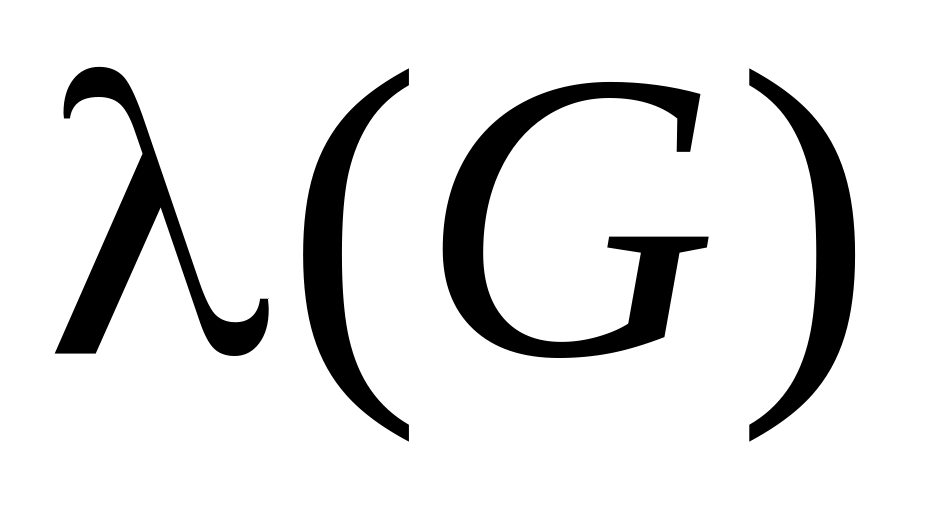графа G называется наименьшее число ребер, удаление которых приводит к несвязному графу.

Примеры.

=0, если граф G несвязен; =1, если в графе G есть мост; , если .

Утверждение. , где  минимальная из степеней вершин графа G.

Доказательство.

1. .

Если =0, то граф G – несвязен, поэтому =0. Пусть >0. отметим те ребер, которые нужно удалить, чтобы граф G разделился на несколько компонент связности. На каждом из этих ребер отметим произвольно по одной вершине. Всего будут отмечены не более вершин.

Удалим отмеченные вершины. Вместе с ними будут удалены все отмеченных ребер, так что граф G распадется. Возможно, что для разделения графа на несколько компонент связности требуется удалить ещё меньше вершин. Значит, .

2. .

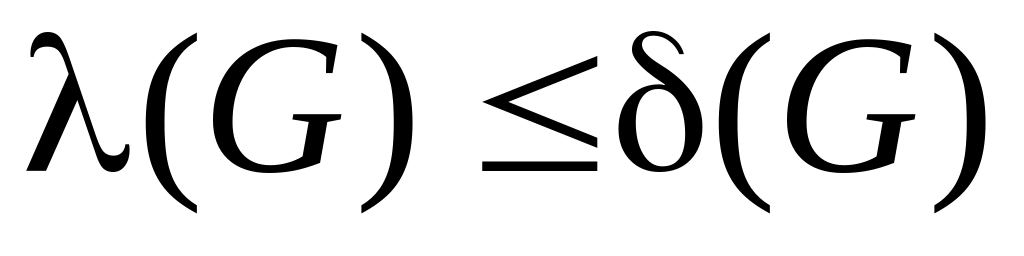Если в графе G есть изолированная вершина, он несвязен, =0. Если >0, то, после удаления ребер, инцидентных вершине наименьшей степени, она станет изолированной, превратится в отдельную компоненту связности. Возможно, что для разделения графа G на две компоненты связности, требуется удалить ещё меньше ребер, поэтому .