256

5.3.1. Мосты и их свойства

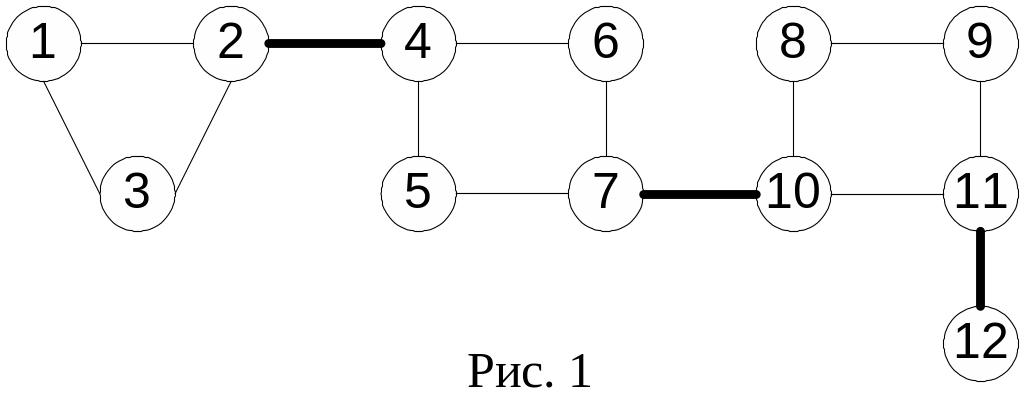
Определение. Мостом (рис. 1) называют такое ребро графа , что его удаление из графа увеличивает на единицу число компонент связности. Другими словами, вершины и и v перестают быть связными. На рис.1 мосты – это ребра (2, 4), (7, 10), (11, 12).

Теорема о свойствах мостов.

Пусть G = (V,E) связный граф, – ребро данного графа. Тогда следующие утверждения эквивалентны

1. е – мост.

2. е не принадлежит никакому простому циклу.

3. е – единственная простая цепь, соединяющая вершины и и v.

4. Множество вершин V можно разбить на два пересекающихся подмножества V₁ и V₂ так, что 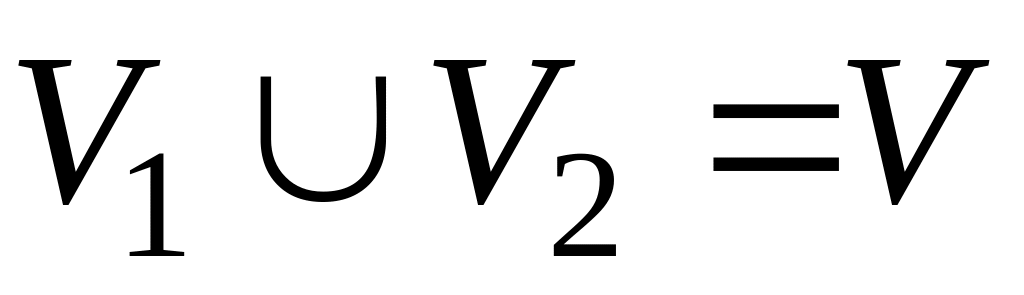, , , и всякая простая цепь, соединяющая любую вершину c любой вершиной , проходит через ребро е.

Доказательство.

1 2. Дано: – мост.

Доказать: Ребро е не принадлежит никакому простому циклу.

Пусть е принадлежит циклу (рис. 2), но тогда его удаление не нарушит связности вершин u и v – противоречие.

2 3. Дано: ребро е не принадлежит никакому простому циклу.

Доказать: е – единственная простая цепь, соединяющая вершины и и v.

Допустим, что существует другая простая цепь, соединяющая вершины и и v. Если объединить ее с ребром е, получится цикл, проходящий через ребро е, – противоречие.

3 4. Дано: е – единственная простая цепь, соединяющая вершины и и v.

Доказать: Множество V вершин можно разбить на два пересекающихся подмножества в соответствии с условием 4.

Удалим из графа ребро е – единственную простую цепь, соединяющую вершины и и v. Связь между вершинами будет разорвана, они окажутся лежащими в разных компонентах связности. Обозначим их (и V₁) и (v V₂). Тогда , .

Пусть , . Так как исходный граф G был связен, в нем существовали простые цепи, соединяющие вершины и . Все они исчезли после удаления е. Значит, все они через ребро е проходили.

4 1. Дано: Выполняется утверждение 4.

Доказать: – мост.

Так как и , то любая простая цепь, соединяющая вершины и и v, проходит через ребро е, значит, его удаление разрывает связь между этими вершинами.

5.3.2. Деревья

Определение. Деревом называют связный граф без циклов. Лесом называют граф без циклов.

На рис. 3 показан лес, состоящий из четырех деревьев.

Теорема о свойствах деревьев.

Пусть – простой граф с р вершинами и q ребрами. Следующие утверждения эквивалентны

1. – дерево.

2. Любые две вершины графа соединены единственной простой цепью.

3. – связен и каждое его ребро – это мост.

4. – связен и число ребер графа G на единицу меньше числа вершин, .

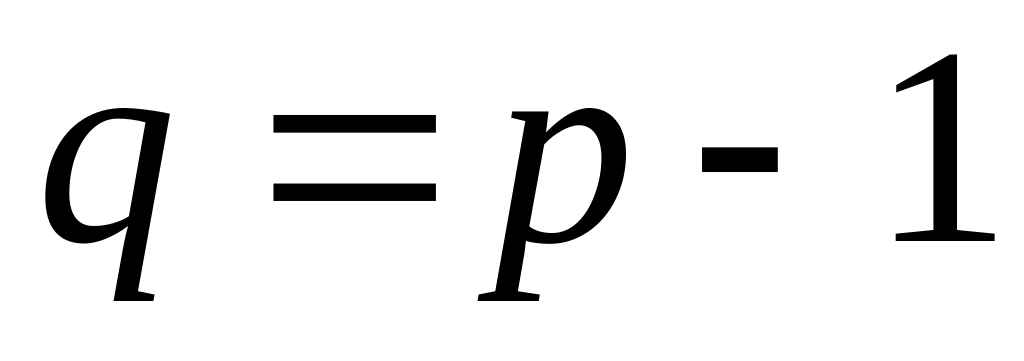5. не содержит циклов и .

6. не содержит циклов, но добавление в граф любого ребра приводит к появлению единственного цикла, который проходит через добавленное ребро.

Доказательство.

1 2. Дано: – дерево.

Доказать: любые две вершины графа соединены единственной простой цепью.

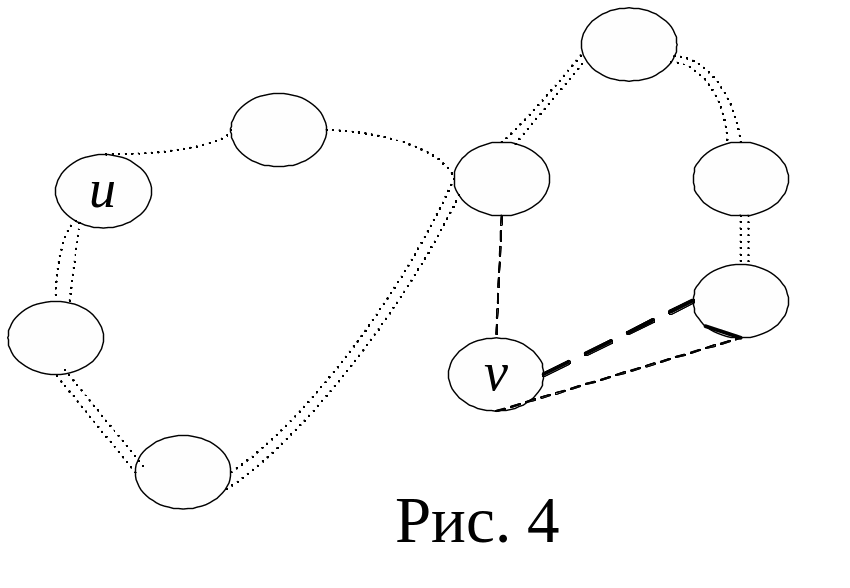
Дерево – это связный граф без циклов. Пусть u, v  произвольные вершины дерева. Если бы существовали две простые цепи, соединяющие вершины u и v, то они образовали бы цикл (рис. 4) – противоречие.

2 3. Дано: любые две вершины графа соединены единственной простой цепью.

Доказать: – связен и каждое его ребро – это мост.

Если любые две вершины графа соединены простой цепью, то граф связен. Пусть вершины v₁, v₂ соединены ребром е. Значит, ребро е – единственная простая цепь, соединяющая v₁ с v₂, следовательно, е - мост.

3 4. Дано: граф связен и каждое его ребро – это мост.

Доказать: граф связен и число его ребер на единицу меньше числа его вершин, .

Доказательство проведем методом математической индукции по числу

вершин графа.

База. Пусть . Единственный вариант – это граф . Тогда , q = 1, .

Индуктивное предположение. Пусть для всякого связного графа с числом вершин , в котором каждое ребро – мост верно соотношение .

Индуктивный переход. Рассмотрим произвольный граф с числом вершин , каждое ребро которого – мост. Удалим любое ребро. Граф распадется на две компоненты связности. Пусть в одной из них р₁ вершин и q₁ ребер; во второй – р₂ вершин и q₂ ребер.

В силу индуктивного предположения ,

4 5. Дано: граф – связен, и число ребер в нем на единицу меньше числа вершин.

Доказать: не содержит циклов.

Фактически мы доказали, что во всяком дереве число ребер . Допустим, что граф содержит цикл. Но удаление любого ребра, принадлежащего циклу, не нарушает связности графа. Будем удалять ребра циклов до тех пор, пока не разрушим все циклы графа. В результате получим связный граф без циклов, то есть дерево, с числом ребер , где . Но и в исходном графе . Значит, , в графе не было ребер, принадлежащих циклам.

5 6. Дано: граф не содержит циклов и

Доказать: граф не содержит циклов, но добавление в граф любого ребра приводит к появлению единственного цикла, который проходит через добавленное ребро.

Если добавленное ребро е не принадлежит никакому циклу, оно является мостом. Тогда исходный граф (без ребра е) не был связен. Будем добавлять в граф мосты, пока компоненты связности не сольются в связный граф без циклов, т.е. – дерево. Число ребер в этом дереве равно . Но и в исходном графе . Таким образом, . В граф нельзя добавить ни одного моста. Тогда любое добавленное ребро – не мост, оно принадлежит некоторому циклу, которого не было в исходном графе. Если бы в графе появились два цикла, проходящие через ребро е, то удаление ребра е не привело бы к исчезновению циклов.

6 1. Дано: граф не содержит циклов, но добавление в граф любого ребра приводит к появлению единственного цикла, который проходит через добавленное ребро.

Доказать. Граф – дерево.

Допустим, что граф не связен. Тогда любое ребро, соединяющее вершины из разных компонент связности, является мостом. А мост не принадлежит никакому циклу – противоречие.

Следствие. Всякое дерево содержит по крайней мере две висячие вершины.

Доказательство. Предположим, что некоторое дерево содержит одну висячую вершину или вовсе их не содержит. Тогда степени по крайней мере вершины графа не меньше 2. Воспользуемся теоремой Эйлера: , что противоречит равенству