1. Синтез и анализ систем. Схема эволюционного синтеза сложных систем.

Система – целостное, органично единое образование, состоящее из

множества элементов, находящихся в отношениях или связях друг с другом.

Задача анализа состоит в изучении свойств системы, если определены:

1. характеристики внешней среды, а также любых структурных и

параметрических неопределенностей и возмущений в виде упорядоченного набора данных ω∈Ω;

2. структура w ∈W и параметры v∈V варианта системы Swv ∈S;

3. оценочное отображение вида K: S×Ω→ Un , где Un – множество

значений оценочной функции, описывающей набор из n показателей эффективности.

Задача синтеза заключается в выборе оптимальных, в известном смысле, структуры и/или параметров при заданных характеристиках внешней среды и налагаемых ограничениях. Ее постановка предполагает определение:

1. множества характеристик внешней среды Ω , описывающее в общем случае любые возмущения внешнего и внутреннего характера;

2. ресурсные (физические) ограничения, определяемые отображением Q:S→H^m и уровнем удовлетворения m h0 ∈H^m ( H^m – множество, каждый элемент которого содержит набор из m внешних параметров системы);

3. критериальные ограничения в виде отображения K: S×Ω→ Un и отображения K0:Ω→ Un ;

4. правило предпочтения Rп в виде бинарного отношения порядка («быть лучше») на Un , обладающее свойствами рефлексивности, транзитивности и антисимметричности.

В рамках системного подхода при решении задачи синтеза

обычно руководствуются следующими принципами и приемами:

1. Сочетание декомпозиции, композиции и иерархичности.

2. Выделение нескольких этапов создания системы, фиксирующих

переход на новый уровень рассмотрения.

3. Всестороннее рассмотрение взаимодействия системы с элемента-

ми внешней среды.

4. Всестороннее рассмотрение основных видов взаимодействия

внутри системы между ее элементами.

5. Сочетание различных качественных и количественных методов

исследования.

6.Генетический анализ и учет предыстории развития данного класса

систем

7. Учет возможности изменения исходных данных и даже содержа-

ния решаемой задачи в ходе многоэтапного процесса создания системы.

Перечисленные принципы и подходы составляют основу эволюционной технологической схемы процесса реального синтеза сложной

системы.

Она базируется на введении иерархии слоев – уровней сложности

принятия решений в условиях априорной неопределенности, в рамках

которых фиксируются промежуточные параметры решения общей задачи

по частям и которая содержит:

1. Слой выбора (генерации) множества неопределенностей и альтернативных стратегий

2. Слой обучения или адаптации

3. Слой самоорганизации

2. Типы отношения подобия систем и моделей. Имитационная модель: основные этапы разработки.

Модели классифицируются по типам реализуемых в них отношений подобия. Эти отношения должны обеспечивать, с одной стороны, подобие в рассматриваемом аспекте исследования, а, с другой стороны, максимальную степень независимости по отношению к не рассматриваемым аспектам.

Абстрактная (закрытая) система – не имеет физических каналов связи с внешней средой.

Физическая (реальная) система взаимодействует тем или иным образом с внешней средой и доступна наблюдению.

Четыре типа отношений моделирования – четыре типа моделей в зависимости от природы исходной и моделирующей ее системы.

Имитационная модель (ИМ) − это формальное (то есть выполненное на некотором языке) описание логики функционирования исследуемой системы и взаимодействия ее элементов во времени, учитывающее наиболее существенные причинно-следственные связи, присущие системе, и обеспечивающее проведение статистических экспериментов.

Имитационная модель позволяет разрешить главную проблему современной науки − проблему сложности или, как еще говорят, − «проклятие размерности».

Существо процесса имитационного моделирования сводится к следующим основным фазам.

1. Построение математического описания процессов и подпроцессов преобразования информации в системе, состоящего из совокупности аналитических моделей различного характера и используемого формализма.

Такое описание называется общей математической моделью

системы.

2. Построение набора алгоритмов, обеспечивающих имитацию всех подпроцессов в соответствии с составляющими математической модели и с логикой причинно-следственных связей, имеющей место в реальной системе.

Организованная в единое целое совокупность алгоритмов, ими-

тирующих процессы, происходящие в системе, называется общим

моделирующим алгоритмом.

3. Реализация на ЭВМ программы имитации и статистического анализа эффективности системы, ее отладка, тестирование и эксплуатация.

Реализованный на ЭВМ комплекс программ для имитации поведения и исследования свойств системы называется имитационной моделью.

Применение методологии ИМ целесообразно в следующих ситуациях.

1. Не существует законченной постановки задачи на исследование и идет процесс познания объекта моделирования.

2. Характер протекающих в системе процессов достаточно сложен и не позволяет описать эти процессы в аналитической форме.

3. Необходимо наблюдать за поведением системы (или отдельных ее компонентов) с изменением (замедлением или ускорением) скорости протекания процессов.

4. При изучении новых ситуаций в системе или при оценке функционирования ее в новых условиях, о которых мало что известно.

5. В случаях, когда требуется изучить поведение системы в условиях, недоступных для исследователя (космические, геофизические условия и т.п.).

6. При подготовке специалистов и освоении новой техники (многочисленные тренажеры).

Методология ИМ, наряду с несомненными достоинствами, имеет ряд недостатков.

1. Разработка и эксплуатация ИМ требует, как правило, больших затрат времени и сил и обходится дороже, чем аналитические исследования.

2. Имитационная модель значительно менее «объективна», чем аналитическая модель, и, зачастую, не точна, причем исследователь не всегда в состоянии оценить степень этой неточности.

3. Использование ИМ создает обманчивое впечатление достоверности, реальности происходящего, тогда как в разрабатываемом для моделирования продукте всегда присутствуют ошибки, поиск которых достаточно сложен и занимает много времени.

4. Данные ИМ всегда носят частный характер (в пределах задаваемых вариантов исходных данных) и требуют дополнительной обработки и интерпретации с целью получения общих выводов и заключений.

3. Общая схема метода Монте-Карло. Принципы организации модельного времени и квазипараллелизма систем.

Метод статистических испытаний (метод Монте-Карло) – численный метод решения математических задач.

Метод статистического моделирования (дальнейшее развитие метода Монте-Карло) – метод исследования процессов функционирования и оценки эффективности сложных систем со стохастическими элементами.

В основе метода статистического моделирования лежит выполнение следующих действий.

1. Проведение большого количества одинаковых по исходным данным актов имитации вероятностного процесса функционирования системы во взаимодействии с внешней средой;

2. Формирование на этой основе соответствующего количества независимых реализаций случайных величин, характеризующих те или иные исходы функционирования системы в смысле выполнения возлагаемых на нее функций (целей);

3. Усреднение и иная статистическая обработка формируемых реализаций случайных величин с целью получения статистически значимых выводов относительно эффективности системы.

Математические основания метода определяются законами больших чисел и предельными теоремами теории вероятностей.

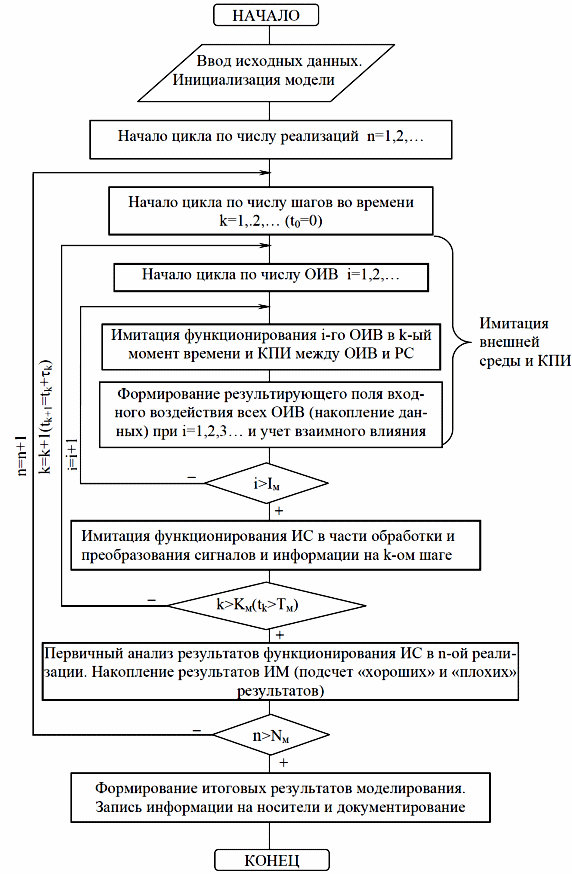
Организация модельного времени

При построении ИМ используют три представления о времени:

1. реальное время системы, работа которой имитируется на модели;

2. модельное время, по которому организуется синхронизация событий в модели системы;

3. машинное время имитации, отражающее затраты ресурса времени ЭВМ на организацию имитации.

Модельное время вводится для синхронизации последовательности событий, происходящих в модели системы, и организации «квазипараллелизма» при имитации одновременного функционирования компонентов системы.

В силу дискретного характера функционирования компьютера текущее время в ИМ задается путем дискретного (скачкообразного) приращения временных отрезков.

Два основных способа задания модельного времени:

1. способ «Δt », при котором приращение модельного времени (продвижение во времени) осуществляется с постоянным шагом Δt;

2. способ «Δz », при котором приращение модельного времени производится в момент наступления очередного события, заключающегося в скачкообразном изменении состояния любого из элементов системы.

Выбор способа задания модельного времени весьма важен с точки зрения рационального использования вычислительного ресурса в ЭВМ, достижения требуемой точности моделирования и сложности моделирующего алгоритма.

4. Стратегическое планирование. Факторный анализ и уравнения линейной регрессии. Полный факторный план

Стратегическое планирование совокупности экспериментов, различающихся по исходным данным, в ходе которых должна быть получена вся необходимая информация о системе, то есть определены все интересующие исследователя свойства. Математическая постановка и решение задачи стратегического планирования (СП) базируется на использовании методов факторного и регрессионного анализа.

1.Факторы 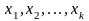– независимые входные переменные – характеристики исследуемой системы 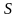и внешней среды , определяющие в своей совокупности параметры, условия и режимы ее функционирования.

2.Каждый из факторов 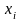имеет диапазон допустимых значе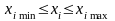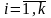ний , . Каждый фактор может принимать в эксперименте несколько значений , , называемых уровнями.

3.Каждому фиксированному набору уровней соответствует определенная точка в многомерном ( -мерном) пространстве, называемом факторным пространством.

4. Фиксированный набор факторов и уровней определяет вариант построения системы и описания внешней среды, одновременно представляя условия проведения или полный набор исходных данных для одного из возможных имитационных экспериментов.

5. Отклики (реакции) системы – зависимые выходные переменные, характеризующие изучаемые свойства системы и зависящие от основных факторов.

В ходе планирования эксперимента должны быть определены:

1) необходимый набор факторов, влияющих на исследуемую характеристику системы и описание зависимостей откликов от факторов;

2) установление количества уровней факторов и их значений в ходе проведения эксперимента;

3) определение количества и порядка проведения экспериментов в виде плана, содержащего комбинации уровней различных факторов.

Регрессионный анализ - метод, обеспечивающий подбор функциональной зависимости заданного вида, при которой экспериментальные точки ложатся на нее наилучшим образом в смысле критерия наименьших квадратов.

Соотношения для коэффициентов линейной регрессии

Требуется найти оценки коэффициентов b₀,...,b_k по результатам наблю-

дения совокупности откликов системы y₁,..., y_N в ходе N экспериментов ,

считая, что полученные данные удовлетворяют линейной регрессии

y₁ = b₀ x₀₁+ b₀ x₀₁ +...+ b₀ x₀₁ + ,

…

y _N = b₀ x_0N + b₁ x_1N +...+ b_k x_kN+ ,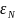

где x_ij , i =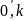 ; j =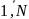 − значения факторов в ходе экспериментов; ,

j = − случайные погрешности определения отклика c нулевым мате-

матическим ожиданием и дисперсию .

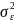Столбцы матрицы X ортогональны, то есть =0,l ≠ r , 0 ≤ r ,l ≤ k .

Коэффициенты регрессии определяются в виде: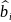 = ,i= ;

Если теперь пронормировать факторы:

X_i^* = (x_i – x_i0 ) / Δx_i , x_i0 = x_imin + Δx_i ; Δx_i = (x_imax − x_imin ) / 2 , то условия ортогональности будут выполняться, если уровни факторов в

ходе эксперимента будут взяты симметрично относительно начала координат и равны +1 и −1.

Такой план эксперимента называется ортогональным N = .

Если осуществляют все возможные сочетания уровней факторов, то

получают так называемый полный факторный эксперимент (ПФЭ).

Полный факторный план при двух уровнях называют еще планом D или

планом – 2^k .

Пример формирования матрицы планирования при k = 2

5. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке среднего

Тактическое планирование – планирование конкретного модельного эксперимента при фиксированных исходных данных.

При фиксированных исходных данных модельный эксперимент состоит из серии повторяющихся имитаций процесса функционирования системы, что позволяет получить усредненную картину относительно ее эффективности с учетом случайного характера протекающих процессов и явлений.

Тактическое планирование сводится к решению двух типов задач:

1. Определение начальных условий в той мере, в какой они влияют на установление стационарного режима работы модели;

2. Снижение погрешности (дисперсии) получаемых при моделировании оценок реакции системы при одновременном сокращении объема испытаний (числа прогнозов).

Первая задача тактического планирования в рамках рассмотренных подходов решается с использованием, в основном, эвристических приемов, опирающихся на знание физики разыгрываемых в ИМ процессов.

Вторая задача тактического планирования может быть решена строго математически. Это решение сводится к определению гарантированного объема испытаний (размера выборки, числа прогонов) для получения требуемой точности оценивания компонентов отклика системы, описывающих ее эффективность.

Снижение или исключение влияния начального периода времени при переходе в установившийся режим должно осуществляться при проведении каждого прогона модели. При этом используют три основных способа:

1. увеличение длительности каждого прогона так, чтобы влияние переходного периода было бы заведомо незначительным;

2. исключение из рассмотрения начального периода (введение этапа предварительной «раскрутки» процесса имитации);

3. искусственный подбор близких к режимным начальных условий для каждой реализации.

Соотношения для требуемого объема испытаний в модельном эксперименте при оценке среднего

Предположим, сначала, что ошибка оценки отклонения в каждой реализации распределена по гауссовскому или нормальному закону. Неравенство эквивалентно следующему неравенству:

Отсюда следует, что величину доверительного интервала можно определить, используя t-статистику или распределение Стьюдента с k-степенями свободы

Z – нормально распределенная величина с нулевым средним и единичной дисперсией;V – независимая от случайная величина, имеющая степенями свободы;

независимые случайные величины, распределенные по нормальному закону Величина отношения в

подчиняется распределению Стьюдента с n-1 степенями свободы.

Реальное использование полученных соотношений в ИМ осно-вано на проведении пробной оценки доверительного интервала или введении правила автоматического останова процесса имита-ции для получения интересующей точности.

При n>30 t-распределение хорошо аппроксимируется гауссовским. При этом

Предположение о нормальности распределения ошибок оценки отклика в каждой реализации может быть неверным. Тогда используется неравенство Чебышева

6. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке дисперсии (1,2,3).

См. первую часть пятого вопроса + продолжение этого вопроса

Исходное неравенство можно переписать в виде

, .

Величина подчиняется распределению с степенями свободы. Если 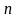достаточно велико, то ее можно рассматривать как распределенную по нормальному закону с параметрами , . Соответственно, можно переписать неравенство в виде

,

где величина распределена по стандартному гауссовскому закону. Отсюда

.

Итоговые уравнения, связывающие 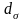и , имеют вид

, , .

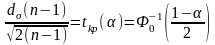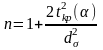7. Тактическое планирование. Соотношения для требуемого объема испытаний в модельном эксперименте при оценке вероятности события (1,2,3).

См. первую часть пятого вопроса + продолжение этого вопроса

Оценка дискретной случайной величины (вероятности события)

В ходе ИМ часто оценивают вероятности или процентные отношения для компонентов отклика, описывающих наступление того или иного события (исхода функционирования системы).

Случайная величина 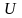в каждой реализации может принимать два значения: единица с вероятностью «хорошего» исхода и ноль с вероятностью «плохого» исхода .

В качестве оценки вероятности выступает величина

,

где – количество интересующих исходов в реализациях.

Требуется по методу доверительных интервалов найти число испытаний, при котором

,

где – доверительный интервал.

Можно переписать исходное неравенство 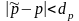в виде

.

Величина подчиняется биномиальному распределению

, .

При и или можно пользоваться гауссовской аппроксимацией величины с параметрами . Отсюда получим:

Итоговые уравнения, связывающие и , имеют вид

, .

Чтобы избавиться от неизвестного значения , можно заменить произведение на величину .

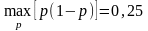В результате получаем выражения для гарантированных значений и

, .

8. Датчики случайных чисел. Алгоритмы моделирования равновероятной и гауссовской случайных величин (1,2,3).

Датчик случайных чисел - алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению.

Базовым алгоритмом является алгоритм датчика стандартной равномерно распределенной случайной величины:

Алгоритмический способ генерации РСВ

В основе алгоритмического способа лежит формирование псевдослучайной последовательности чисел с использованием рекуррентного алгоритма вида

где F(...) – нелинейная функция, реализующая отображение

Главным требованием к функции F(...)является «плотная» заполняемость области A×A – «единичного» квадрата: чем более плотно заполняется квадрат, тем более «не предсказуемым» является очередное значение αi+1 по сравнению с предыдущим значением αi.

Распространенной версией является следующий алгоритм

Алгоритм генерации гауссовской случайной величины

Алгоритм реализует генерацию значений гауссовской стандартной величины (ГСВ) ξ , имеющей параметры

Работа алгоритма основывается на результатах центральной предельной теоремы, согласно которой сумма n значений одинаково распределенных и независимых случайных величин имеет в пределе (при n →∞) гауссовское распределение.

Имея датчик РСВ, значение ξ может быть получено как

где αi – независимые значения равномерной случайной величины α, получаемые при последовательных обращениях к датчику РСВ. Величину n достаточно выбирать порядка 10...20. В вычислительном отношении удобно выбирать n = 12 , тогда получается простейший алгоритм генерации ГСВ

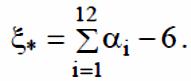
9. Моделирование случайных величин с произвольным законом распределения (1,2,3).

Метод нелинейного функционального преобразования. Особенностью данного метода является то, что он может использоваться для генерации величин, заданных аналитическим видом закона распределения.

Теорема.

Пусть случайная величина α имеет равномерное распределение в интервале [0, 1]и связана со случайной величиной ξ соотношением

где f (u) – некоторая функция, удовлетворяющая указанным свойствам.

Тогда случайная величина ξ имеет плотность распределения вероятностей вида f (u) и может быть найдена на основе обратного функционального преобразования

Для доказательства найдем функцию распределения ξ. Используем тот факт, что при f (u) > 0 величина α монотонно возрастающая функция ξ.

Также и ξ в этом случае монотонно возрастающая функция α. Тогда для функции распределения ξ выполняется следующая цепочка равенств:

Очевидно, что Fξ(y) = ϕ(y) , что и требовалось доказать, так как это
означает, что ξ имеет плотность распределения вида f (u) (fξ(u) = f (u)).
Таким образом, последовательность случайных чисел ξi с таким
распределением можно получить из соотношения вида

где α_i − последовательность значений РСВ, получаемых при обращении к датчику α.

П ример. Пусть − закон Релея. Тогда

Ф ункциональная связь величин ξ и α определяется соотношением

При непосредственной генерации можно использовать более экономное соотношение

так как величина 1−α также имеет равномерное распределение на интервале [0, 1].

Метод исключений (метод Фон-Неймана). Особенностью данного метода является то, что он может использоваться для генерации величин, заданных как аналитическим видом закона распределения, так и эмпирически полученными распределениями.

Теорема.

Пусть функция g(x) ≥ 0 и на ее основе определено множество значений вещественных переменных G ={(x, y), 0 ≤ y ≤ g(x)}.

П усть совместная плотность распределения случайных величин ξ и η на множестве значений G равна

то есть имеет равномерный вид.

Т огда плотность распределения вероятностей случайной величины ξ равна

У чтем, что для функции распределения ξ выполняется

Отсюда следует доказательство теоремы, так как

Для получения алгоритма моделирования используют следующие построения.

Пусть имеется достаточно эффективный способ моделирования совместно равновероятных случайных величин в области значений G₁ , накрывающей требуемую область G:

G₁ ={(x, y), 0 ≤ y ≤ g₁(x), g₁(x) ≥ g(x)}.

g(x)

М	G1(x)	g1(x)
		g(x)

х

а	G(x)	b

Рис. 3.6. Иллюстрация метода исключений

Тогда для генерации случайной величины с законом распределения f_ξ (x) = g(x)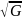 требуется выполнить следующую последовательность действий:

1. Генерируется по равномерному закону в пределах G₁ случайная точка с координатами (ξ_i , η_i ) .

2. Если η_i ≥ g(ξ_i ) , то полученная точка исключается из рассмотрения

• осуществляется возврат на первый шаг.

3. Если η_i < g(ξ_i ) , то ξ_i используется в качестве очередного значения

искомой случайной величины.

Простым вариантом выбора множества G₁ является задание

g₁ = M = max g(x) , a ≤ x ≤ b ,

x

a , b − границы интервала, в пределах которого функция g(x) локализуется практически полностью.

Тогда получаем простейший алгоритм генерации.

1. ξ_i = a +(b −a)α′_i , η_i = α′′_iM , где α′_i , α′′_i − независимые значения, получаемые на основе стандартного датчика РСВ.

2. Если η_i ≥ g(ξ_i ) , то осуществляем переход на шаг 1, иначе запоминаем ξ_i в качестве очередного значения ξ.

Рассмотренные методы и алгоритмы генерации случайных величин имеют как самостоятельное значение для построения моделирующего алгоритма ИМ, так и могут использоваться в алгоритмах генерации случайных процессов и случайных полей (случайных функций времени и случайных функций координат).

10. Понятие математической схемы. Модель общей динамической системы и операторы «вход-состояние-выход», классификация математических схем (1,2,3)

Математическая схема – стандартное (типовое) звено при переходе от содержательного к формализованному на математическом языке описанию системы с учетом воздействий внешней среды.

«Описательная (концептуальная) модель» – «математическая схема» – «моделирующий алгоритм» – «имитационная модель».

Определение: математической схемой называется частная математическая модель преобразования сигналов и информации некоторого элемента системы, определяемая в рамках конкретного математического аппарата и ориентированная на построение моделирующего алгоритма данного класса элементов сложных систем.

Математическая модель сложной системы состоит из математических схем (моделей), описывающих функционирование элементов, и математической схемы (модели) взаимодействия между элементами.

Модель общей динамической системы (ОДС), описывается множествами следующих величин:

1. совокупностью входных воздействий:

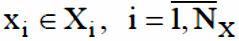
2. совокупностью воздействий внешней среды:

3. совокупностью внутренних параметров:

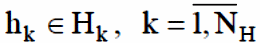
4. совокупностью выходных реакций:

Индексирующее множество моментов времени t∈T.

Независимые (экзогенные) переменные

Зависимые (эндогенные) переменные

Закон функционирования ОДС описывается оператором вида Fs

где – реализации (траектории) процессов на предшествующем

интервале времени

Закон функционирования может быть задан в виде функции, функционала, логических условий, в табличной форме, а также в виде словесного правила соответствия.

Практическое использование модели ОДС весьма проблематично: слишком велика степень абстракции и обобщения.

При разработке математических моделей, ориентированных на последующее использование при имитационном моделировании элементов сложных систем, используются типовые математические схемы, реализующие более конкретные проблемно-ориентированные формы математического описания.

11. Типовые математические схемы, используемые при построении модели элементов сложных систем (D,F,P,Q)

Непрерывно-детерминированные модели (D-схемы (dynamic system))

Подход применяется в ситуациях, когда объект моделирования не включает элементов случайности (они не учитываются), а его функционирование осуществляется в непрерывном времени.

Типовой математической схемой является схема, описываемая обыкновенными дифференциальными уравнениями

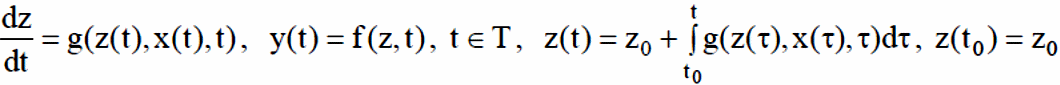
z(t)∈Z –состояние системы; x(t)∈X – детерминированное входное воздействие; y(t)∈Y – выходная реакция системы.

D-схема определяется совокупностью данных:

Математическая модель объекта в данном случае практически полностью определяет и его моделирующий алгоритм, который в ЭВМ сводится к реализации процедуры численного или аналитического интегрирования обыкновенного дифференциального уравнения.

Дискретно-детерминированные модели – F-схемы(finit automat)

Подход применяется для описания объектов при отсутствии стохастических возмущений, а их функционирование осуществляется в дискретном времени. Типовой математической схемой является модель конечного автомата, называемая F-схемой. Множества значений входных воздействий X, внутренних состояний Z и выходных реакций Y являются конечными и имеют I , J , K элементов

Функционирование конечного автомата осуществляется в дискретные моменты времени t = 0,1,2,...

Описание процесса преобразования информации осуществляется с помощью отображений вида

Автомат первого рода (автомат Мили)

Автомат второго рода (автомат Мура y(t) = ψ(z(t))

F- схема окончательно определяется совокупностью данных

Дискретно-стохастические модели – P-схемы (probabilistic automat)

Подход применяется для описания объектов при наличии стохастических возмущений и процессов, а их функционирование осуществляется в дискретном времени.

Типовой математической схемой является схема вероятностного автомата или P-схема. Реализуется вероятностный характер переходов: из каждого состояния zi (t) под воздействием входного сигнала xk (t) могут осуществляться переходы во все состояния {z j(t +1)} с определенными вероятностями {pj ≥ 0}.

P-автоматом называется объект, определяемый четверкой

– семейство I×K матриц размерности J×J

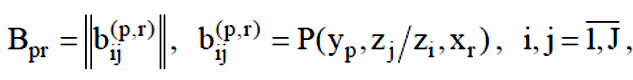
– вероятности начальных состояний z(0) в момент t0 .

Вероятностный автомат Мили

Вероятностный автомат Мура

Задание вероятностных автоматов может быть проведено в табличном виде или в виде графов, дополненных соответствующими значениями ненулевых вероятностей переходов и выходов.

Имитационное моделирование элементов, описываемых на основе P-схем, реализуется на основе алгоритма, определяющего все возможные переходы в соответствии с математической моделью и включающего также процедуру генерации случайной составляющей переходов для соответствующих вероятностей.

Математическая схема стохастического конечно-разностного уравнения

Непрерывно-стохастические модели – Q-схемы (queuing system)

При реализации похода имеет место стохастический характер изменения состояний объекта моделирования, а процессы перехода «вход- состояние-выход» описываются в непрерывном времени.

Типовая математическая схема системы массового обслуживания – Q-схема. Стандартный объект – элементарный прибор обслуживания (ЭПО); состоит из накопителя (H) заявок и канала (K) обслуживания.

Схема элементарного прибора обслуживания

– входной поток событий (заявок)

– внутренний поток обслуживания

– выходной поток обслуженных или не обслуженных заявок.

Вектор состояний -

– состояние накопителя ( – накопитель пуст,

– в накопителе одна заявка и т.д.);

– состояние канала обслуживания ( – канал свободен, – канал занят).

– алгоритм функционирования, определяющий правила поведения в неоднозначных ситуациях.

– множество внутренних параметров ЭПО (предельная емкость накопителя , интенсивность потока обслуживания).

Q-схема описывается набором данных:

Математическая модель широко используется для описания элементов систем и сетей массового обслуживания потоков событий (заявок) в связи и телефонии, а также для любых информационно-управляющих систем, которые могут рассматриваться как совокупность тем или иным способом соединенных ЭПО.

Построение имитационных моделей с использованием Q-схем имеет специфику и для разработки моделирующего алгоритма требуется использование специальных подходов и методов.

Математическая схема стохастического дифференциального уравнения

12. Математическая модель взаимодействия элементов сложной системы. Формирование одноуровневой схемы сопряжения.

Взаимодействие элементов в процессе функционирования сложной системы рассматривается как результат совокупного воздействия каждого элемента на все остальные.

При формализации процесса взаимодействия оно достаточно полно описывается в рамках механизма обмена сигналами.

Сигналы описывают входные и выходные воздействия и являются физическими носителями передаваемой между элементами информации.

1. Сигналы передаются по каналам связи, проложенным между элементами системы.

2. Действующие в реальной системе физические каналы связи вносят искажения и задержки по времени передачи сигналов.

3. Канал, передающий сигналы мгновенно и без искажения, называется идеальным.

4. Полностью и адекватно формализованная сложная система имеет только идеальные каналы связи.

5. Для описания физических каналов связи в модели вводятся эквивалентные элементы, отражающие возникающие искажения и задержки.

6. В результате введения каждого такого элемента возникает необходимость введения дополнительных идеальных каналов, соединяющий эквивалент с другими элементами.

Модель механизма обмена сигналами как формализованная (математическая) схема взаимодействия элементов системы между собой имеет следующие составляющие:

1. модель формирования выходных сигналов элементов системы;

2. модель сопряжения элементов сетью идеальных каналов связи;

3. модель приема входных сигналов для всех элементов системы.

В качестве математической схемы информационного взаимодействия необходимо рассматривать вторую составляющую механизма обмена сигналами – схему сопряжения элементов, определяющую адресацию характеристик выходных сигналов одних элементов и их компоновку во входные сигналы других элементов.

Математической схемой сопряжения элементов в системе S называется совокупность < X, Y, R > , а оператор R называется оператором сопряжения.

Схема сопряжения < X, Y, R > содержит исчерпывающие сведения о модели взаимодействия и соединении элементов сложной системы.

Такая схема называется одноуровневой в том смысле, что она определяет прямое сопряжение элементов без учета их объединения в подсистемы или функциональные модули.

13. Основные типы систем массового обслуживания. Аналитическое решения для СМО М/М/1/0.

В ходе математической формализации систем как систем или сетей массового обслуживания (СМО) они традиционно представляются в виде композиции элементарных приборов обслуживания (Q-схем), соединенных в соответствии с имеющимися взглядами на облик системы.

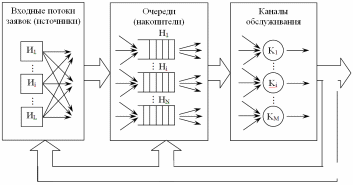
Обобщенная структурная схема СМО

Все СМО делятся на два больших класса:

разомкнутые СМО – функционирование источников и входной поток не зависят от процесса обслуживания (обратной связи нет);

замкнутые СМО – входной поток зависит от числа заявок, находящихся на обслуживании, а заявки с выхода могут опять поступать на вход системы (существует обратная связь).