I. Статика

Задача 1.1. Центр тяжести тел и фигур

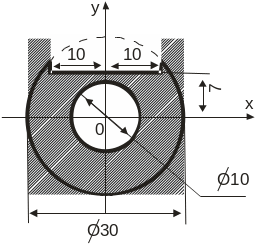
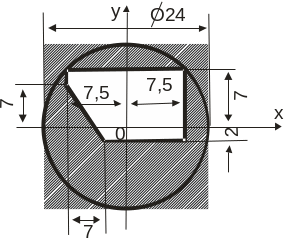
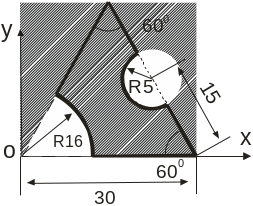
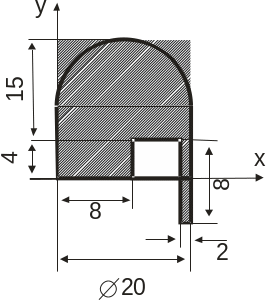
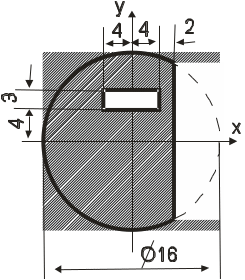
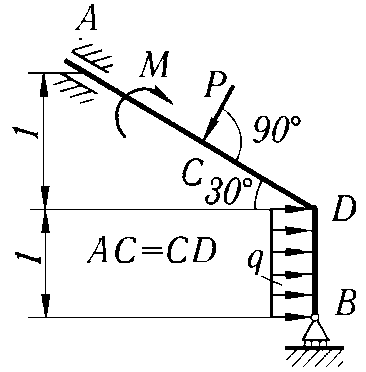
Определить координаты центра тяжести сложной тонкой однородной пластины (табл. 1.1).

Таблица 1.1

Вариант	Пластина	Вариант	Пластина
1		2
3		4
5		6
7		8
9		0

Дополнительные сведения

1. Центр тяжести однородной плоской пластины

, (1.1)

где S – площадь фигуры.

2. Центр тяжести площади треугольника – точка пересечения медиан:

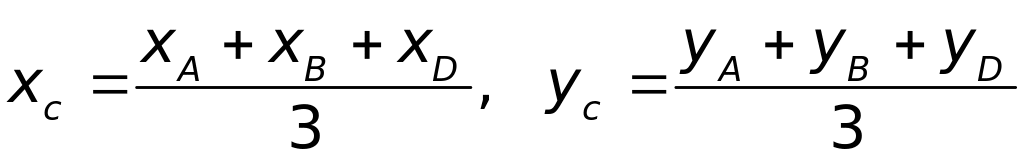, (1.2)

где x_A, x_В, x_D, y_A, y_В, y_D – координаты вершин треугольника в выбранной системе координат.

Рис 1.2. Центр тяжести площади треугольника

3. Центр тяжести дуги окружности лежит на оси симметрии Ох:

, (1.3)

где R – радиус дуги окружности, α – половина центрального угла в радианах.

Рис. 1.3. Центр тяжести дуги лежит на оси симметрии

4. Центр тяжести площади кругового сектора лежит на оси симметрии Ох:

, (1.4)

где R – радиус сектора, α – половина центрального угла в радианах.

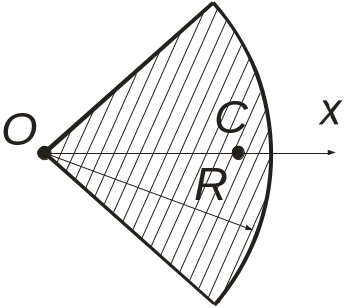
Рис. 1.4. Центр тяжести кругового сектора

Пример выполнения задания

Определить координаты центра тяжести сложной тонкой однородной пластины, изображённой на рисунке 1.1, если OB = ОА = ОЕ = OF = 30 см, r = 30 см, OB₁=R = 60 см.

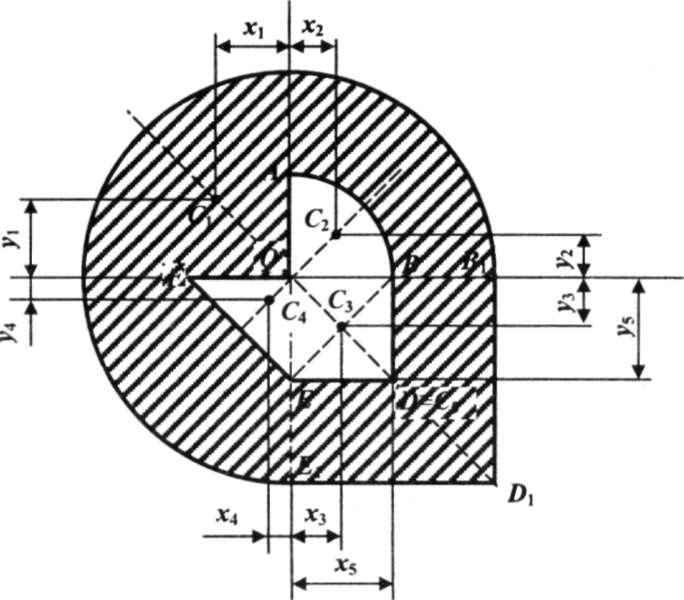
Рис. 1.5. Расчётная схема примера

Для решения задачи применяется метод дополнений. Разбиваем пластину на простейшие фигуры, центры тяжести которых можно вычислить:

1. сектор ОЕ₁В₁;

2. сектор ОАВ;

3. прямоугольник ОВДЕ;

4. треугольник OEF;

5. прямоугольник OB₁D₁E₁.

Вычисляем площади (S_k) выделенных фигур:

, ,

, , .

Используя формулу (1.4), определяем расстояния ОС₁, ОС₂ и координаты точек С₁, С₂:

,

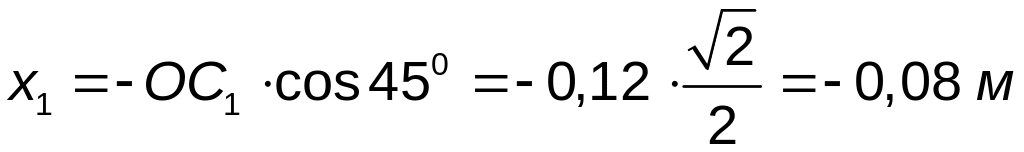, y₁ = OC₁·cos 45⁰=0,08 м,

,

x₂ = y₂ = OC₂·cos 45⁰=0,12 м.

Координаты точки С₃: x₃ = 0,15 м, у₃ = - 0,15 м.

Координаты точки С₄ определяются по формуле (1.2)

x₄ = - 0,1 м, y₄ = - 0,1 м.

Координаты точки С₅ (совпадает с точкой D)

х₅ = 0,3 м, у₅ = - 0,3 м.

Координаты центра тяжести всей пластины определяются по формулам (1.1)

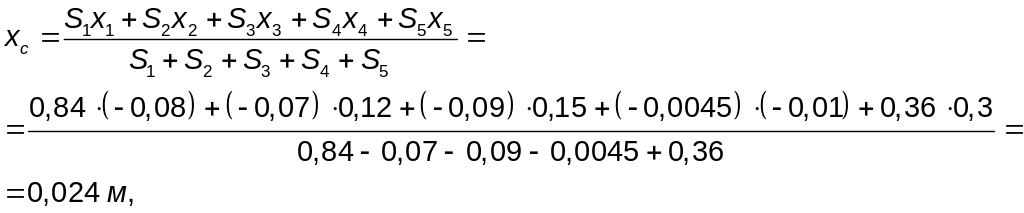
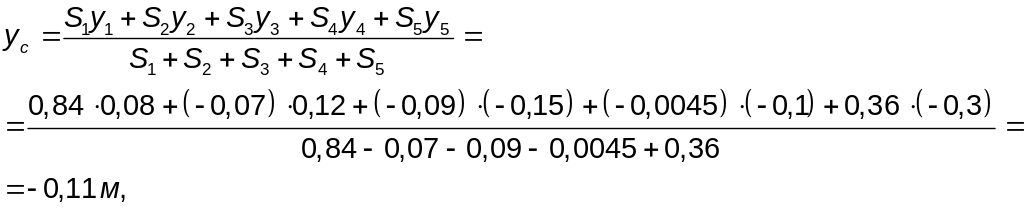
Ответ, x_c = 0,024 м, у_с = - 0,11 м.

Задача 1.2. Определение реакции опор твёрдого тела

Таблица 1.2

Вариант	Данные варианта	Схема варианта
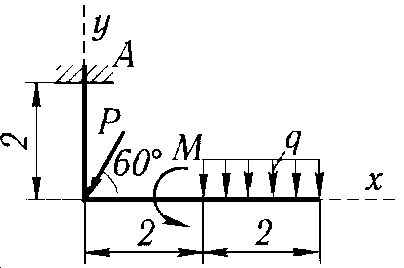
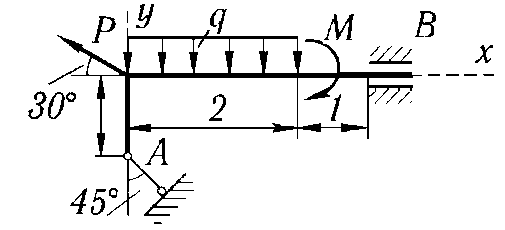
1	Р = 10 кН, М = 6 кН·м, q = 2 кН/м
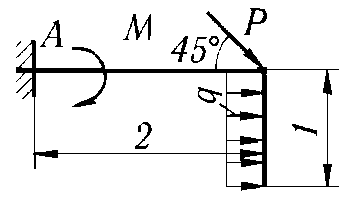
2	P = 20 кН, М = 5 кН·м, q = 2 кН/м
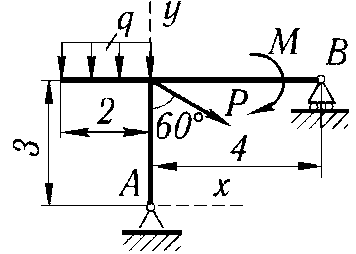
3	P = 15 кН, М = 8 кН·м, q = 1 кН/м
4	P = 5 кН, M = 2 кН·м, q = 1 кН/м
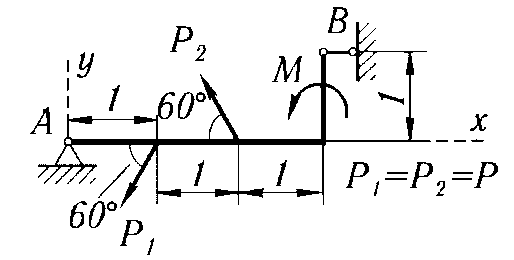
5	P = 10 кН, М = 4 кН·м, P1 = P2 = P
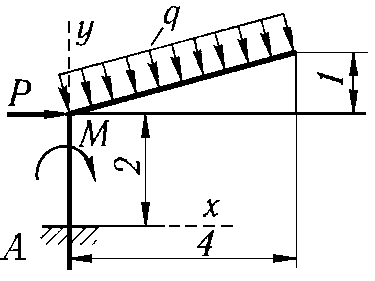
6	P = 6 кН, M = 2 кН·м, q = 1 кН/м
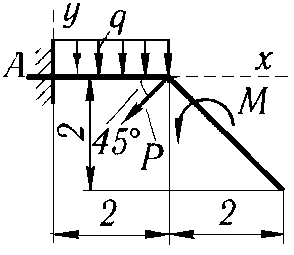
7	P = 2 кН, M = 4 кН·м, q = 2 кН/м
8	P = 20 кН, М = 10 Кн·м, q = 4 кН/м
9	P = 10 кН, M = 6 кН·м
0	P = 2 кН, M = 4 кН·м, q = 2 кН/м

Образец выполнения задания

Д а н о: схема закрепления бруса

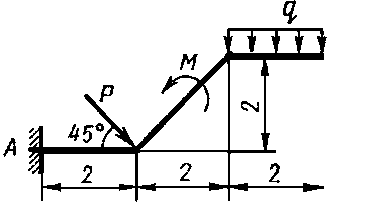
Рис. 1.6. Схема примера

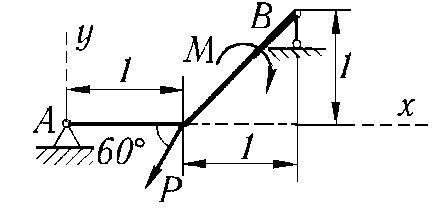
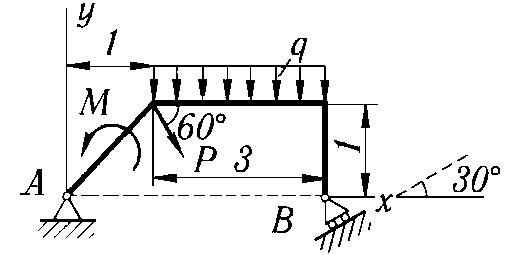
P = 5 кН; M = 8 кН·м; q = 1,2 кН/м. Определить реакции опор.

Решение. Рассмотрим систему уравновешивающих сил, приложенных к конструкции. Действие связей на конструкцию заменим их реакциями (рис. 1.7). Равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей Q = q·2 = 2,4 кН.

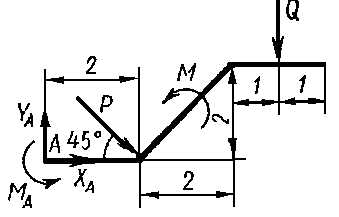
Рис. 1.7. Расчётная схема примера

Составим таблицу 1.3 проекций сил и моментов

Таблица 1.3

Силы	XA	YA	P	Q	M	MA
Проекция на ось Ох	XA	0	P·cos450	0	–	–
Проекция на ось Оy	0	YA	P·sin450	- Q	–	–
Момент относительно точки А	0	0	- P·sin450·2	- Q·5	M	MA

После составления таблицы проекций и моментов легко составить уравнения равновесия

X_A + P·cos 45° = 0,  (1.5)

Y_A + P·sin 45° − Q = 0,  (1.6)

- P·sin 45°·2 − Q·5 + M + M_A = 0.  (1.7)

Из уравнения (1.5) находим X_A = − P·cos 45° = −2,5· .

Из уравнения (1.6) находим Y_A = − P·sin 45° + Q = −2,5· + 2,4 ≈ − 1,14.

Из уравнения (1.7) находим M_A = − M + Q·5 + P·sin 45°·2 ≈ 11,1.