12. Нахождение общего решения линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами методом неопределенных коэффициентов.

Рассмотрим линейное неоднородное дифференциальное уравнение (л.н.д.у.) 2-го порядка

Ly=y′′(x)+py′(x)+qy(x)=f(x), a<x<b, (1)

где p,q∈R , f(x) -- заданная непрерывная на промежутке (a,b) функция.

Рассмотрим соответствующее к (1) линейное однородное дифференциальное уравнение (л.о.д.у.)

Ly=y′′(x)+py′(x)+qy(x)=0. (2)

Для построения общего решения дифференциального уравнения (1) достаточно найти одно частное решение самого линейного неоднородного дифференциального уравнения (1). Частное решение линейного неоднородного дифференциального уравнения (1) можно найти, например, методом подбора или методом неопределенных коэффициентов в зависимости вида функции f(x).

Теорема. Если правая часть f(x) линейного неоднородного дифференциального уравнения (1) имеет вид

где P_k(x) и Q_m(x) - заданные многочлены соответственно степени k и m, α и β - заданные действительные числа, то линейное неоднородное дифференциальное уравнение (1) имеет своим частным решением функцию

где A_p(x) и B_p(x) - полные многочлены степени p, p=max{k,m}, s≥0 -- кратность корня α+iβ

соответствующего характеристического уравнения.

На практике записывают многочлены A_p(x) и B_p(x) с неопределенными коэффициентами, подставляют в исходное дифференциальное уравнение и приравнивают коэффициенты в обеих частях при выражениях вида

13. Линейная зависимость и линейная независимость системы функций на отрезке [а, b]. Определитель Вронского.

Функции y₁(x), y₂(x), ..., y_n(x), определённые на отрезке [a;b], называются линейно зависимыми на [a;b] , если существуют постоянные α₁, α₂, ..., α_n , не равные нулю одновременно и такие, что α₁y₁(x) + α₂y₂(x) + ... + α_ny_n(x) = 0 для всех x из отрезка [a;b].

В противном случае функции y₁(x), y₂(x), ..., y_n(x) называются линейно независимыми.

Линейную зависимость и линейную независимость функций определяют также на (a;b) , (a;b] , [a;b) , на бесконечных промежутках.

Справедливо следующее утверждение.

Функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является линейной комбинацией других на этом отрезке .

Справедливо следующее утверждение.

Функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других .

Очевидны следующие утверждения.

• Если среди функций y₁(x), y₂(x), ..., y_n(x) есть нулевая функция, то функции линейно зависимы.

• Если функции y₁(x), y₂(x), ..., yk(x) линейно зависимы, то при любых yk + 1(x), yk + 2(x), ..., y_n (x) функции y₁(x), y₂(x), ..., yk(x), yk + 1(x), ..., yn(x) также линейно зависимы.

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри [a;b] .

• Если функции y₁(x), y₂(x), ..., y_n(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок [а;b] (если, они определены на этом отрезке).

Вектор–функции Y₁(x), Y₂(x), ..., Y_n(x),

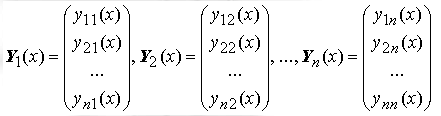
называются линейно зависимыми на отрезке [a;b] , если существуют постоянные α₁, α₂, ..., αn , не равные нулю одновременно и такие, что

α₁ Y₁(x) + α₂ Y₂(x) + ... + α_n Y_n(x) = 0

для всех x из отрезка [a; b].

В противном случае функции Y₁(x), Y₂(x), ..., Y_n(x) называются линейно независимыми.

Определитель Вронского (вронскиан).

Пусть функции непрерывны вместе с своими производными (до n - 1 порядка включительно) на интервале (a, b). Определитель Вронского (вронскиан) указанной системы функций задаётся следующей формулой:

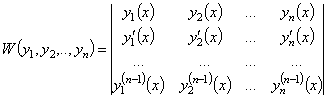
Для того, чтобы функции были линейно независимыми на (a, b), достаточно, чтобы хотя бы в одной точке интервала (a, b). Отметим, что это условие является достаточным, но не необходимым. Т.е., если для всех значений переменной из интервала , то про линейную зависимость функций в общем случае ничего определённого сказать нельзя.