Интегральные кривые дифференциальных уравнений 1-го порядка
9. Дифференциальные уравнения 2-го порядка. Общее и частное
решение. Начальные условия. Теорема существования и единственности решения задачи Коши.
Теорема. Если в уравнении
y(n)=f(x, y, y`, y``, …, y(n-1))
функция f(x, y, y`, y``, …, y(n-1)) и ее частные производные по аргументам x, y, y`, y``, …, y(n-1) непрерываны в некоторой области, содержащие значения
х=х0, у=у0, y`=y`0, …, y(n-1)=y0(n-1)
то существует, и причем единственное, решение у=у(х) уравнения, удовлетворяющее условиям
y│х-х0=y0, y`│x=x0=y`0,…, y(n-1)│x=x0=y0(n-1) (2)
Эти условия называются начальными условиями.
Если рассматривать уравнения второго порядка
y``=f(x, y, y`)
то начальными условиями при х=х0 для решения будут условия
y=y0, y`=y`0
Общим решением дифференциального уравнения n-го порядка называется функция
зависящая от n произвольных постоянных С1,С2, …, Сn.
y=ɸ(x, C1, C2, …, Cn)
Всякая функция, получающаяся из общего решения при конктретных значениях постоянных С1, С2, называется частным решением.
10. Решение уравнений вида y(n)=f(x); y''=(x,y'); y''=f(y,y')
1 тип. Уравнение вида y(n) = f (x).
Общее решение данного уравнения находится n –кратным интегрированием.
.
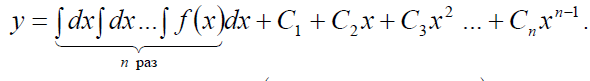2 тип. Уравнение вида F(x, y(k ) , y(k+1) ,..., y(n) )= 0 .
Это уравнение не содержит искомой функции y(x) и ее производных до порядка k −1 включительно. Порядок такого уравнения можно понизить на k единиц заменой z = y(k ) . Здесь функция z рассматривается как новая неизвестная функция от x , то есть z = z(x). При такой замене уравнение примет вид
F(x,z,z′,...,z(n−k ) )= 0.
Если удастся найти общее решение полученного уравнения z = ϕ(x, C1,..., C(n-k)), то общее решение исходного уравнения найдется n -кратным интегрированием уравнения
y(n) = ϕ(x, C1,..., C(n-k)),
3 тип. Уравнение вида F(y, y′, y′′,..., y(n) )= 0 .
Это уравнение не содержит независимую переменную x .
Порядок уравнения можно понизить на единицу, используя подстановку y′ = p . Здесь функция p рассматривается как новая неизвестная функция от y , то есть p = p(y).
Все производные y′′,..., y(n) выражаются через производные от функции p по y . Соответствующие формулы имеют вид:
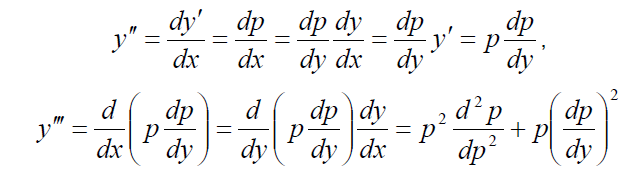
и так далее. Подставив эти выражения для производных в исходное уравнение, получим дифференциальное уравнение (n −1)-ого порядка относительно новой неизвестной функции p(y).
11. Общее решение линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Характеристическое уравнение.
Рассмотрим линейное уравнение n-го порядка
L(y) ≡ y (n) + a1 y (n – 1) + … + an – 1 y ' + an y = f (x), (12.1)
где коэффициенты a1, a2, …, an суть действительные числа, а правая часть f (x) непрерывна в некотором интервале (a, b) (a ≥ – ∞, b ≤ + ∞).
Так как интегрирование неоднородного линейного уравнения приводится к интегрированию соответствующего однородного уравнения, то рассмотрим сначала вопрос о построении общего решения однородного уравнения
L(y) ≡ y (n) + a1 y (n – 1) + … + an – 1 y ' + an y = 0. (12.2)
Для нахождения общего решения этого уравнения достаточно знать фундаментальную систему решений. Так как коэффициенты уравнения постоянны и, следовательно, заведомо непрерывны при всех значениях x, то согласно теореме Пикара и все решения уравнения (12.2) определены при всех значениях x.
Характеристическое уравнение линейного дифференциального уравнения с постоянными коэффициентами
— алгебраическое уравнение, которое получается из данного дифференциального уравнения после замены функции у и её производных соответствующими степенями величины l, т. е. уравнение
К
этому уравнению приходят при отыскании
частного решения вида
для
данного дифференциального уравнения.
Для системы линейных дифференциальных
уравнений
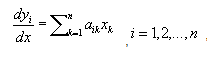
Характеристическое уравнение записывается при помощи определителя
