Глава 2. Теория пределов
2.1 Определение предела последовательности.
Уточним еще раз некоторые моменты.
Определение
1.
Последовательностью
называется упорядоченное счетное
множество чисел
.
Обратите внимание, что
а) всего чисел счетное множество и
б) они расположены в определенном порядке.
Над последовательностями можно проделывать некоторые операции.
а) Умножение последовательности на число.
Пусть
дана последовательность
и число
.
Тогда произведением последовательности
на число
называется последовательность вида
.
б) Сложение и вычитание последовательности
Пусть
даны две последовательности
и
.
Суммой
и
называется последовательность вида
+
=
Разностью - последовательность виды
=
.
в) Умножение и деление последовательностей
Произведение последовательностей
=
.
Частное последовательностей
Определение 2. Последовательность называется
ограниченной
сверху, если
;
ограниченной
снизу, если
ограниченной,
если
.
(Последнее
часто пишут так:
).
А теперь самое важное.
Определение
3.
Говорят, что при
,
стремящемся к бесконечности,
последовательность
сходится к пределу
(запись:
или
)
если
.
Число называют пределом последовательности .
Дадим комментарий к этому важнейшему понятию.
В понятии
«последовательность» впервые в математики
нашло свое отражение движение. До
введения этого понятия математика
изучала лишь статистические объекты
площадь треугольника, 2x2
= 4 и т.д., и только в последовательности
впервые находит свое отражение движение.
Действительно, пусть
это моя координата на оси в какой-то
-
й момент времени. Тогда, идя по
последовательности, я двигаюсь по оси
сначала я нахожусь в точке
,
затем перехожу в точку
,
затем в точку
и т.д.
Конечно, движение бывает различным. Понятие предела отражает один из типов этого движения. Посмотрим еще раз на определение понятия предела, записав его в виде
.
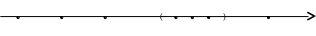
Вокруг точки
взята произвольная
-окрестность
.
Сначала движение может быть произвольным,
но вот на
- м шаге последовательность попадает в
эту
-окрестность
и все последующее движение происходит
в этой
-окрестности,
то есть попав на
- м шаге в окрестность
точки
,
последовательность навсегда остается
в этой окрестности. Так как
сколь угодно мало, то это означает, что
в своем движении мы неограниченно близко
приближаемся к точке
и уже не можем уйти от нее. Понятие
предела и отражает именно такой тип
движения.
Дадим еще несколько похожих определений.
Определение
4. Говорят, что при
последовательность
сходится к пределу, равному
(запись:
или
)
если
.
Это означает, что
какое бы большое число
мы не взяли, при своем движении на каком
- то
шаге мы окажемся правее точки
и при дальнейшем движении всегда будем
находиться правее этой точки.
Определение
5.
Говорят, что при
последовательность
сходится к пределу, равному
(запись:
или
)
если
Попробуйте описать сами движение этой последовательности.
2.2 Бесконечно малые последовательности
Определение
1. Последовательность
называется бесконечно-малой
последовательностью (б.м.п.), если
,
то есть, если
.
Определение
2.
Последовательность
называется бесконечно-большой
последовательностью (б.б.п.), если
(это записывается еще и так:
,
не учитывая знака перед
,
то есть если
.
Изучим некоторые свойства этих последовательностей.
1. Сумма и разность бесконечно-малых последовательностей есть также бесконечно-малая последовательность.
Доказательство.
б.м.п.
.
б.м.п.
.
Возьмем
.
Тогда
,
откуда следует,
что
есть б.м.п.
Следствие. Сумма любого конечного числа б.м.п. ест также б.м.п
2. Произведение б.м.п на ограниченную последовательность есть б.м.п.
Доказательство
ограничена.
б.м.п.
Но тогда
,
отсюда и следует, что
есть б.м.п.
3. Б.м.п. ограничена
Доказательство
Пусть б.м.п. Тогда .
Возьмем
.
Тогда
то есть
ограничена
Следствие. Произведение б.м.п. есть также б.м.п.
4. Пусть
б.м.п. и
.
Тогда
есть б.б.п.
Доказательство
б.м.п
.
Возьмем любое
и положим
.
Тогда
,
отсюда следует, что
есть б.б.п.
5. Пусть б.б..п, тогда есть б.м.п.
б.б.п =>
.
Возьмем любое
и положим
Тогда
,
отсюда следует, что
есть б.м.п.
2.3 Свойства сходящихся последовательностей
Определение.
Последовательность
называется сходящейся, если у нее
существует конечный предел (то есть
существует
и
).
Рассмотрим свойства этих последовательностей.
1. Для того, чтобы
последовательность
была сходящейся, необходимо и достаточно,
чтобы ее можно было представить в виде
,
где
,
а
б.м.п.
Доказательство.
Необходимость. Пусть . Это значит, что
.
Обозначим
.
Тогда
и
то есть
б.м.п.
Достаточность.
Пусть
,
где а
б.м.п., то есть
.
Но так как
,
то
,
то есть
.
Это свойство позволяет почти все остальные свойства свести к свойствам б.м.п.
2. Сходящаяся последовательность ограничена.
Доказательство.
Пусть
,
где
б.м.п. В силу этого
ограничена, то есть
.
Но тогда
,
то есть
ограничена.
3. Если
и
сходящиеся последовательности, то
тоже сходящаяся последовательность и
.
Доказательство.
сходящаяся , где б.м.п.
сходящаяся
,
где
б.м.п.
Но тогда
.
По свойствам
б.м.п.,
есть б.м.п. и поэтому
есть сходящаяся последовательность и
4. Если
сходящаяся последовательность, то
тоже сходится и
.
Доказательство
сходится , где б.м.п.
Но тогда
и, по свойства б.м.п.,
есть тоже б.м.п. Поэтому
сходится и
.
5. Если
и
сходящиеся последовательности, то
тоже сходящаяся последовательность и
.
Доказательство
сходится , где б.м.п.
сходится , где б.м.п.
Но тогда
.
По свойствам
б.м.п.,
,
,
есть б.м.п. Их сумма есть также б.м.п.
Поэтому,
есть сходящаяся последовательность и
.
6. Если
,
то, начиная с некоторого
,
последовательность
ограничена.
Доказательство
сходится
.
Так как
то возьмем
.
Тогда
.
Но тогда
выполняется неравенство
и мы имеем
.
Сравнивая начало и конец, получим, что
и
,
то есть. при
последовательность
ограничена.
7. Пусть
и
сходящиеся последовательности, причем
.
Тогда
есть также сходящаяся последовательность
и
.
Доказательство
сходится , где б.м.п.
сходится , где б.м.п.
Тогда
.
Вспомним, что
.
Тогда
есть б.м.п.,
есть б.м.п и т.к.
ограниченна, то
есть тоже б.м.п.
Итак,
б.м.п.
и поэтому
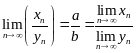
2.4 Предельный переход в неравенствах
Теорема 1. Пусть
сходящаяся последовательность и
.
Тогда
.
Доказательство этой теоремы проведем методом от противного.
Обозначим
.
Тогда утверждение, противоположное
доказываемому, имеет вид:
.
Возьмем
.
Тогда, по определению, предела
последовательности, можно написать
.
Последнее неравенство
распишем в виде двойного:
.
Но так как
,
то
и получается что
,
что противоречит условию теоремы.
Следствие.
Если
и
сходящиеся последовательности и
,
то
.
Доказательство дается следующей цепочкой следствий
Важное замечание.
Допустим, что в условии теоремы вместо
мы написали
.
Можно ли утверждать, что
?
Ответ отрицательный.
Действительно, пусть, например,
.
Тогда
,
но
.
Таким образом,
итог этой теоремы и замечание выглядит
так: в неравенствах допустим предельный
переход, надо только иметь ввиду, что
после предельного перехода строгое
неравенство (типа > или <) может
замениться на нестрогое (> перейдет в
,
< перейдет в
).
Теорема 2. Пусть