Решение.

Показатель	1994	1995	1996	1997	1998	1999	2000	2001	2002
До, дни	98	97	86	82	74	71	65	58	42

Проанализируем данный ряд динамики, используя следующие показатели:

- цепные и базисные: абсолютные приросты, темпы роста, темпы прироста,

- среднегодовые: абсолютный прирост, темп роста, темп прироста.

Для расчета показателей на переменной базе (цепной способ расчета) каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели называются цепными. При расчете показателей на постоянной базе сравнения (базисный способ расчета) каждый последующий уровень ряда сравнивается с уровнем, принятым за базу. Вычисленные таким образом показатели называются базисными.

Цепные и базисные: абсолютные приросты, темпы роста, темпы прироста определяются по нижеприведенным формулам:

- абсолютный прирост (y) определяется в разностном сопоставлении двух уровней ряда динамики в единицах измерения исходной информации и выражает абсолютную скорость роста (снижения):

y =y_i - y_0i,

где y_i – текущий (сравниваемый) уровень числа зарегистрированных преступлений;

y_0i – предшествующий или базисный уровень числа зарегистрированных преступлений;

i=1,2, 3,…n.

Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного.

- темп роста характеризует относительную скорость роста или снижения уровня ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятого за базу:

;

Если темп роста больше единицы (или 100%), то это показывает на увеличение изучаемого уровня по сравнению c базисным. Темп роста, равный единице (или 100%), показывает, что уровень изучаемого периода по сравнению с базисным не изменился. Темп роста меньше единицы (или 100%) показывает на уменьшение уровня изучаемого периода по сравнению с базисным. Темп роста всегда имеет положительный знак.

- темп прироста (Т_пр) характеризует относительную скорость изменения уровня ряда в единицу времени и вычисляется по формуле:

Тпр_i(%)=Тр_i (%)-100%.

Если уровни ряда динамики сокращаются, то соответствующие показатели темпа прироста будут со знаком минус, так как они характеризуют относительное уменьшение прироста уровня ряда динамики.

Тогда, используя вышеприведенные формулы, сведем имеющиеся сведения и расчеты в таблицу 2.

Таблица 2 – Динамика длительности оборота оборотных средств по годам

Год	Длительность оборота оборотных средств, дни	Абсолютный прирост, дни		Темп роста, %		Темп прироста, %
		цепной	базисный	цепной	базисный	цепной	базисный
1994	98	-	-	-	-	-	-
1995	97	-1	-1	98,97	98,97	-1,03	-1,03
1996	86	-11	-12	88,65	87,75	-11,35	-12,25
1997	82	-4	-16	95,34	95,34	-4,66	-4,66
1998	74	-8	-24	90,24	86,04	-9,76	-13,96
1999	71	-3	-27	95,94	95,94	-4,06	-4,06
2000	65	-6	-33	91,54	87,83	-8,46	-12,17
2001	58	-7	-40	89,23	89,23	-10,77	-10,77
2002	42	-16	-56	72,41	64,61	-27,59	-35,39

Из таблицы видно, что длительность оборота оборотных средств за период 1994 – 2002 гг. сокращается, что является положительной тенденцией в функционировании оборотных средств предприятия, т.е. происходит высвобождение оборотных средств.

Для определения среднегодовых показателей динамики: абсолютный прирост, темп роста, темп прироста воспользуемся следующими формулами:

Средний абсолютный прирост – показатель, характеризующий среднюю абсолютную скорость роста (снижения) уровня за отдельные периоды времени. Он показывает, на сколько единиц увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.д.). Определение среднего абсолютного прироста производится по формуле:

или

Средний темп роста – относительный показатель, выраженный в форме коэффициента и показывающий, во сколько раз увеличился уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежеквартально и т.п.). Среднегодовой темп роста вычисляется по формуле средней геометрической:

, или ,

где m – число коэффициентов роста.

Средний темп прироста – относительный показатель, выраженный в процентах и показывающий, на сколько увеличился (уменьшился) уровень по сравнению с предыдущим в среднем за единицу времени (в среднем ежегодно, ежемесячно и т.п.). Среднегодовой темп прироста получаем, вычтя из среднего темпа роста 100 %:

.

Результаты расчета средних показателей динамики представлены в таблице 3.

Таблица 3 - Среднегодовые показатели динамики длительности оборота оборотных средств за 1994 – 2002 гг.

Показатель	Метод расчета	Значение
1. Средний уровень ряда ( )		дней
2. Средний абсолютный прирост ( )		дней
3. Средний темп роста ( )
4. Средний темп прироста ( )		89,95 – 100 = -10,05%

Изучим существующую тенденцию динамики с помощью метода наименьших квадратов.

Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровней явления во времени, свободное от случайных колебаний.

Для того чтобы построить количественную модель, выражающую общую тенденцию изменения уровней динамического ряда во времени, используют аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:

,

где – уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней производится на основе адекватной математической модели, которая наилучшим образом аппроксимирует (отображает) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть обоснован в теоретическом анализе, выявляющем характер развития явления, а также в графическом изображении эмпирических (фактических) уровней ряда динамики (линейной диаграмме).

Общее представление о характере тенденции длительности оборота оборотных средств за период 1994 – 2002 гг. можно получить из графического изображения ряда динамики (рисунок 1).

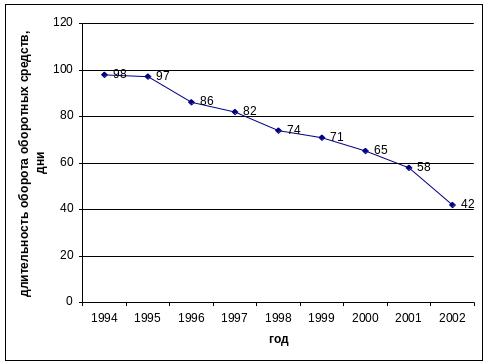
Рисунок 1 - Динамика длительности оборота оборотных средств за 1994 – 2002 гг.

Из рисунка 1 видно, что для изучаемого периода времени (1994 – 2002 гг.) уравнение прямой достаточно полно отображает общую тенденцию развития явления. Выравнивание по уравнению прямой линии используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

В связи с этим, для нахождения уравнения тренда воспользуемся уравнением прямой, которое имеет следующий вид:

= а₀ + а₁x.

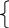С пособ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров а₀ и а₁:

у = nа₀ + a₁t;

tу = a₀t + a₁t²,

где у – исходные (эмпирические) уровни ряда динамики,

n – число членов ряда,

t – обозначение времени.

Решение системы уравнений позволяет получить выражения для параметров а₀ и а₁:

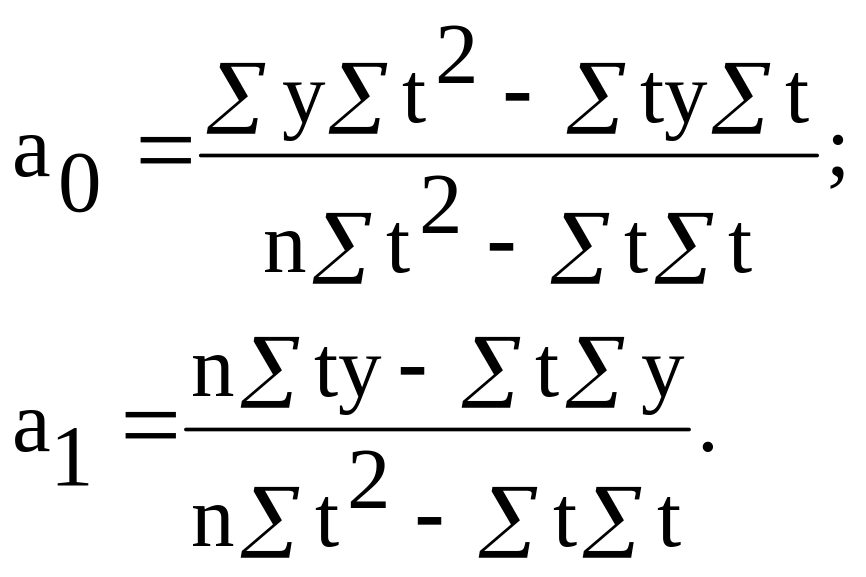
В рядах динамики техника расчета параметров уравнения упрощается, если показателям времени t придают такие значения, чтобы их сумма была равна нулю, т.е. t = 0.

Т.к. число исходных (эмпирических) уровней ряда - нечётное (n = 9), это выполнимо при следующем условии:

,

где k – порядковый номер года (k = 1, 2, …);

n – число лет в периоде.

Тогда построим расчетную таблицу (таблица 4).

Таблица 4 – Расчет показателей времени

Показатель	1994	1995	1996	1997	1998	1999	2000	2001	2002
k	1	2	3	4	5	6	7	8	9
t	-4	-3	-2	-1	0	1	2	3	4

При условии, что t = 0, исходные нормальные уравнения принимают вид: