5) Комплексные частотные характеристики

относятся входные и передаточные функции, записанные в комплексной форме. Входная комплексная функция цепи - это зависимость от частоты комплексного сопротивления  или комплексной проводимости

П ередаточная комплексная функция (коэффициент передачи, системная функция) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме. Предполагается, что в цепи действует одно внешнее воздействие, т. е. цепь содержит один источник воздействия, а другие независимые источники напряжения или тока отсутствуют или не действуют. Различают четыре вида передаточных функций: передаточная функция по напряжению   передаточная функция по току  передаточное сопротивление

п ередаточная проводимость Передаточные функциимогут определяться для различных пар выбранных входных и выходных

выводов цепи.

6) Спектральный анализ сложных периодических сигналов с применением гарм и эксп ряда Фурье.

Ряд Фурье.

с коэффициентами

(2.6)

Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами  кратными основной частоте последовательности.

так что

Подставив эти выражения в (2.5), получим другую, - эквивалентную форму ряда Фурье:

которая иногда оказывается удобнее.

Спектральная диаграмма периодического сигнала.

Рис. 2.1. Спектральные диаграммы некоторого периодического сигнала: а — амплитудная; б — фазовая

Комплексная форма ряда Фурье.

7.Интегральные преобразования Фурье

Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.

Преобразование Фурье функции   вещественной переменной является интегральным и задаётся следующей формулой:

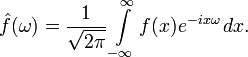
Математический смысл преобразования Фурье состоит в представлении сигнала у(х) в виде бесконечной суммы синусоид вида F(v)sin(vx). Функция F(v) называется преобразованием Фурье или интегралом Фурье, или Фурье-спектром сигнала.

8.Основные теоремы спектрального анализа, спектральная плотность произведения и скалярного произведения сигналов.

Спектр суммы сигналов (теорема линейности) равен сумме спектров этих сигналов.

Это свойство является следствием линей­ности преобразования Фурье. В более общем виде оно может быть записано следующим образом:

где a_k — коэффициенты разложения; 

Сдвиг сигнала во времени f(t—t₀) соответствует умножению его спектра на   :

Из (9.28) следует важный вывод о том, что при сдвиге сигнала во времени его амплитудный спектр не изменяется, а фазовый изме­няется пропорционально wt₀. Эта теорема имеет большое значение, так как в процессе обработки сигналов часто возникает необходи­мость осуществлять задержку сигнала

Изменение масштаба независимого переменного (сжатие сиг­нала) описывается выражением

сжатие сигнала во времени (а > 1) приво­дит к расширению спектра сигнала и напротив — растяжение сиг­нала (а < 1) — к сужению спектра.

Перемножение двух сигналов (теорема свертки). Спектр про­изведения двух функций f₁(t) и f₂(t) соответствует свертке их спектров F₁(jw) и F₂(jw):

Дифференцирование и интегрирование сигнала. При дифферен­цировании сигнала его спектр

умножается на оператор jw:

а при интегрировании делится на jw:

Смещение спектра сигнала на частоту   соответствует умно­жению сигнала на оператор   :

Спектральная плотность произведения сигналов.

Спектральная плотность произведения двух сигналов с точностью до постоянного числового множителя равна свертке спектральных плотностей сомножителей:

операция свертки коммутативна,

Скалярное произведение сигналов. 

Энергия суммы двух произвольных сигналов u(t) и v(t) определяется выражением

E =  [u(t)+v(t)]² dt = E_u + E_v + 2 u(t)v(t) dt

Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию

E_uv = 2 u(t)v(t) dt.

Интеграл выражения для двух вещественных сигналов является фундаментальной характеристикой, пропорциональной взаимной энергии сигналов. Его называютскалярным произведением сигналов

П_uv = (u(t),v(t)) = u(t)v(t) dt = ||u||*||v|| cos 

Линейное пространство сигналов с таким скалярным произведением называется гильбертовым пространством Н.