Модель безопасности Клементса (с полным перекрытием) Вероятностные модели.

Модели этого типа исследуют вероятность преодоления системы защиты за определенное время Т. К достоинствам моделей данного типа можно отнести числовую оценку стойкости системы защиты. К недостаткам — изначальное допущение того, что система защиты может быть вскрыта. Задача модели — минимизация вероятности преодоления системы защиты.

Примером вероятностной модели является модель безопасности с полным перекрытием.

Модель безопасности с полным перекрытием

Идеи управления рисками во многом восходят к модели безопасности с полным перекрытием, разработанной в 70-х годах.

Модель системы безопасности с полным перекрытием строится исходя из постулата, что система безопасности должна иметь, по крайней мере, одно средство для обеспечения безопасности на каждом возможном пути воздействия нарушителя на ИС.

В модели точно определяется каждая область, требующая защиты, оцениваются средства обеспечения безопасности с точки зрения их эффективности и их вклад в обеспечение безопасности во всей вычислительной системе.

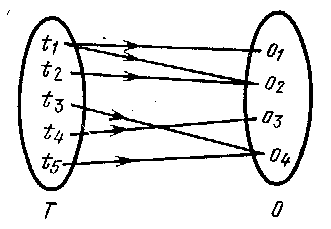
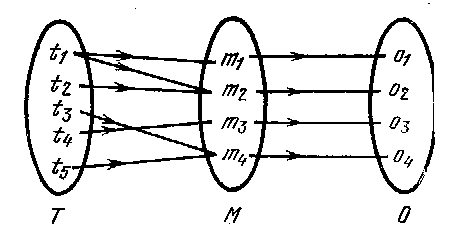
Рис.1. Двудольный граф «угроза- объект».

Рис.2. Трехдольный граф «угроза - средство безопасности - объект».

Считается, что несанкционированный доступ к каждому из множества защищаемых объектов (ресурсов ИС) О сопряжен с некоторой «величиной ущерба» для владельца ИС, и этот ущерб может быть определен количественно.

С каждым объектом, требующим защиты, связывается некоторое множество действий, к которым может прибегнуть нарушитель для получения несанкционированного доступа к объекту. Потенциальные злоумышленные действия по отношению ко всем объектам oO формируют набор угроз ИБ Т. Каждый элемент множества угроз характеризуется вероятностью появления.

Множество отношений “объект—угроза” образуют двухдольный граф (рис. 1), в котором ребро (t_i,о_j) существует тогда и только тогда, когда t_i является средством получения доступа к объекту o_j. Следует отметить, что связь между угрозами и объектами не является связью типа «один к одному» - угроза может распространяться на любое число объектов, а объект может быть уязвим со стороны более чем одной угрозы. Цель защиты состоит в том, чтобы «перекрыть» каждое ребро данного графа и воздвигнуть барьер для доступа по этому пути.

Завершает модель третий набор, описывающий средства обеспечения безопасности М, которые используются для защиты информации в ИС. В идеальном случае, каждое средство m_kM должно устранять некоторое ребро (t_i,o_j). В действительности, m_k выполняет функцию «барьера», обеспечивая некоторую степень сопротивления попыткам проникновения. Это сопротивление - основная характеристика, присущая всем элементам набора M. Набор М средств обеспечения безопасности преобразует двудольный граф в трехдольный (рис.2).

В защищенной системе все ребра представляются в форме (t_i,m_k) и (m_k,o_j). Любое ребро в форме (t_i,o_j) определяет незащищенный объект. Следует отметить, что одно и то же средство обеспечения безопасности может противостоять реализации более чем одной угрозы и (или) защищать более одного объекта. Отсутствие ребра (t_i,o_j) не гарантирует полного обеспечения безопасности (хотя наличие такого ребра дает потенциальную возможность несанкционированного доступа за исключением случая, когда вероятность появления t_i равна нулю).

Далее в рассмотрение включается теоретико-множественная модель защищенной системы - система обеспечения безопасности Клементса. Она описывает систему в виде пятикортежного набора S={О,T,M,V,B}, где

О - набор защищаемых объектов;

Т - набор угроз;

М - набор средств обеспечения безопасности;

V - набор уязвимых мест - отображение Т×O на набор упорядоченных пар V_i=(t_i,o_j), представляющих собой пути проникновения в систему;

В - набор барьеров - отображение V×M или Т×О×М на набор упорядоченных троек b_i=(t_i,o_j,m_k) представляющих собой точки, в которых требуется осуществлять защиту в системе.

Таким образом, система с полным перекрытием - это система, в которой имеются средства защиты на каждый возможный путь проникновения. Если в такой системе  (t_i,o_j)V, то  (t_i,o_j,m_k)В.

Далее производятся попытки количественно определить степень безопасности системы, сопоставляя каждой дуге весовой коэффициент.

Модель системы безопасности с полным перекрытием описывает требования к составу подсистемы защиты ИС. Но в ней не рассматривается вопрос стоимости внедряемых средств защиты и соотношения затрат на защиту и получаемого эффекта. Кроме того, определить полное множество «путей проникновения» в систему на практике может оказаться достаточно сложно. А именно от того, как полно описано это множество, зависит то, насколько полученный результат будет адекватен реальному положению дел.

Вывод

К достоинствам моделей дискретного доступа можно отнести относительно простую реализацию. В качестве примера реализации данного типа моделей можно привести так называемую матрицу доступа, строки которой соответствуют субъектам системы, а столбцы — объектам; элементы матрицы характеризуют права доступа.

К недостаткам относится "статичность модели". Это означает то, что модель не учитывает динамику изменения состояния ВС, не накладывает ограничений на состояния системы.

Основное преимущество вероятностных моделей состоит в возможности численного получения оценки степени на­дежности системы защиты информации. Данный метод не специфицирует непосредственно модель системы защиты информации, а может использоваться только в сочетании с другими типами моделей систем защиты информации.

При синтезе систем защиты информации данный под­ход полезен тем, что позволяет минимизировать накладные расходы (ресурсы вычислительной системы) для реализа­ции заданного уровня безопасности. Модели данного типа могут использоваться при анализе эффективности внешних по отношению к защищаемой системе средств защиты ин­формации. Ярким примером применимости данной модели является анализ на ее основе вероятности вскрытия за ко­нечный временной промежуток средств защиты, предлагае­мых для системы MS-DOS. Для систем защиты, построенных на основании других моделей, данная модель может приме­няться для анализа эффективности процедуры идентифика­ции / аутентификации.

При анализе систем защиты информации модели дан­ного типа позволяют оценить вероятность преодоления сис­темы защиты и степень ущерба системе в случае преодоления системы защиты.