3. Построение концептуальной модели сложной системы и ее формализация

При структурном подходе к моделированию системы в ней выде­ляются три автономные группы блоков: имитирующие воздействие внешней среды Е на систему S, являющиеся моделью процесса функ­ционирования системы S; вспомогательные, служащие для машинной реализации блоков первых групп, а также для фиксации и обработки резул ьтатов мод ел и рован ия.

Описание свойств процесса функционирования системы S, т.е. ее концептуальной модели М_к, может быть наглядно представлено в виде совокупности некоторых элементов, условно изображенных квадрата­ми на рис. 1.2. Эти квадраты представляют собой описание некоторых подпроцессов исследуемого процесса функционирования системы 5, воздействия внешней среды Е и т.д. Переход от описания системы к ее модели сводится к исключению из рассмотрения некоторых второстепен­ных элементов описания (элементы 5...8,39...41, 43...47). Предполагает­ся, что они не оказывают существенного влияния на ход процессов, исс­ледуемых с помощью модели. Часть элементов (14, 15, 28, 29, 42) заме­няется пассивными связями Л,, отражающими внутренние свойства си­стемы. Некоторая часть элементов (1...4, 10, 11, 24, 25) заменяется входными факторами х и воздействиями внешней среды у,. Возможны

комбинированные замены, например, элементов 9. 18, 19, 32, 33 пас­сивной связью h₂ ^и воздействием v₂ внешней среды Е. Элементы 22,23,

36, 37 отражают воздействие у системы на внешнюю среду.

Оставшиеся элементы системы S группируются в блоки Sj S_r/ S_Jir отражающие процесс функционирования исследуемой сис­темы. Каждый из этих блоков достаточно автономен, что выражается

в минимальном количест­ве связей между ними. 11о- всденис этих блоков долж­но быть хорошо изучено, и для каждого из них постро­ена математическая мо­дель, которая в свою оче­редь может содержать ряд подблоков. Построенная блочная модель процесса функционирования иссле­дуемой системы S пред­назначена для анализа ха­рактеристики этого про­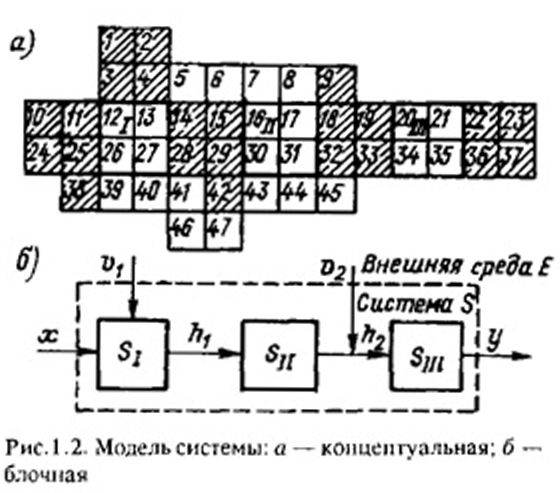

цесса, который может быть проведен при машинной реализации полученной модели.

После перехода от описания моделируемой системы S к ее концеп­туальной модели М_к, необходимо построить математические модели

процессов, происходящих в различных блоках.

Для иллюстрации возможности такой формализации рассмотрим процесс функционирования некоторой гипотететической системы S, которую можно разбить на т подсистем с характеристиками y₁ (t), y₂ (t), … y_ny (t) c параметрами h₁, h₂, … h_nH при наличии

входных воздействий x₁, x₂, … x_nX и воздействий внешней среды v₁, v₂, … v_nV Тогда математической моделью процесса может слу­жить система соотношений вида

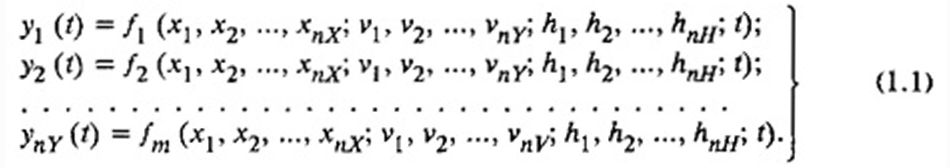
Если бы функции f₁, f₂, … f_n были известны, то соотношения

(1.1) оказались идеальной математической моделью процесса функци­онирования системы S.

Однако на практике получить модель достаточно простого вида для больших систем чаще всего невозможно. Поэтому обычно процесс фун­кционирования системы разбивают на ряд элементарных подпроцес­сов. При этом необходимо так проводить разбиение отдельных подпро­цессов, чтобы не возникало трудностей при их формализации. Для моделирования процесса функционирования системы S на ЭВМ необ­ходимо преобразовать математическую модель процесса в соответству­ющий моделирующий алгоритм и машинную программу.