Глава III - Метод линейного приближения

§ 3.1 Некоторые алгебраические неравенства.

Один из вариантов неравенства Коши-Шварца.

Если тогда ≥

Доказательство:

Возведём левую часть под общий знаменатель, раскроем скобки в правой части и переведём правый знаменатель налево, а левый направо. Получаем:

≥

≥ =>

=> ≥

Задача 1:

Пусть a,b,c>0; a+b+c=1. Доказать следующие неравенства и найти обобщенную форму.

1) 2) 3)

Решение:

1) первое неравенство в цепочке

получено из неравенства Коши-Шварца. Последнее неравенство после сокращения имеет вид, ≤ которое верно.

2) Первое неравенство очевидно. Если заменим ,тогда второе неравенство будет таким :

оба слагаемых неотрицательные так как <

3)Среди чисел найдутся два таких, что их сумма будет не больше . Это всегда возможно, иначе следующее неравенства будут верны: > , > ,

> Если мы сложим эти неравенства, получим => > это неравенство не верно. Поэтому не умаляя общности допускаем, что < .

Наще основное неравенство может быть записано в следующей форме:

Теперь мы можем доказать что если мы заменим тройку чисел на в последнем неравенстве, то левая часть не возрастет:

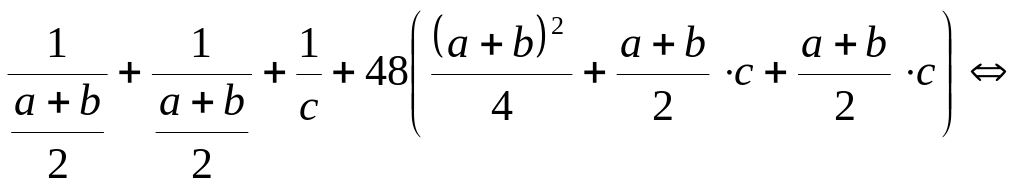
Так как тогда достаточно доказать, что которое верно, как мы установили .Мы доказали, что наше основное неравенство достаточно доказать для тройки чисел

Если мы обозначим а то наше основное неравенство имеет вид

Неравенство доказано и равенство имеет место при , и перестановки этого набора.

Примечание к задаче№1: Легко доказать, что все неравенства имеют одну форму: когда . Если мы подставим в последнем неравенстве , мы получим

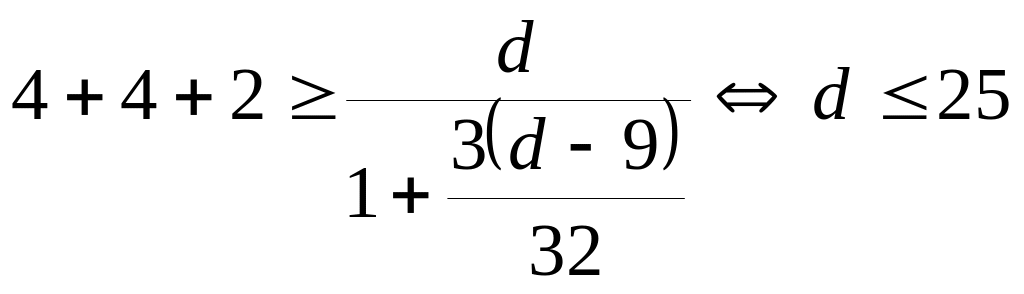
Итак, наше неравенство верно только для чисел 0<d≤25. Так же если 0<d≤25, то следующее неравенство верно:

≥ ≥ 0.

Итак достаточно проверить случай d=25, но мы дали для решения задачи № 1 независимые решения.

И еще одно замечание относительно случая d=25. Любые попытки использовать классические методы будут безрезультатными, так как там есть случай равенства кода a,b,c не равны между собой. Такие неравенства могут быть решены методом подсчета, но мы нашли элементарное решение не используя подсчеты. Эти неравенства могут быть сформулированы, не используя условие a+b+c=1.

Альтернативная формулировка: пусть a, b, c > 0

1. Докажите неравенство ,

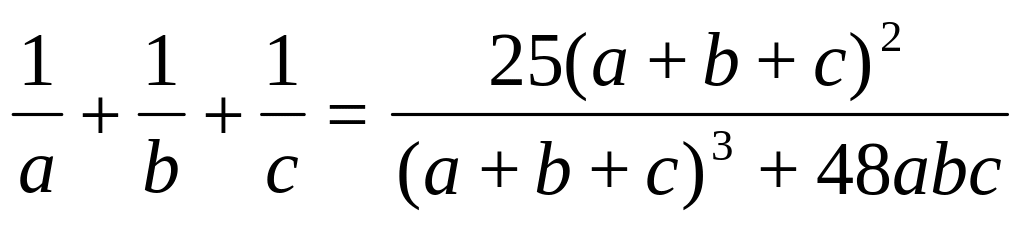2. Для какого положительного числа d следующее неравенство верно для всех a, b, c > 0.

≥ .

Решение: Это неравенство однородное для всех значений a, b, c. Так оно может быть нормализовано путем замены a+b+c=1 и мы придем к задаче 1.

Аналогично, неравенство для двух неизвестных a, b > 0; a+b=1 => ≥ верно для всех d>0. Но если там 3 неизвестных, сложность задачи сильно увеличивается.

Задача 2.Допустим a,b,c,x,y,z > 0 и abc=xyz. Докажите что

≥ .

Решение: упростив мы получаем : acx+ axy + aby+ byz + bcz+cxz ≥ 3(abc + xyz); Используя среднее арифметическое- среднее геометрическое неравенство мы получим acx+aby+bcz≥ . Аналогично axy-byz+cxz≥ 3xyz. Суммировав последние два неравенства приходим к следующему: решению.

Примечание:

Это неравенство имеет свою геометрическую интерпретацию, например, это следует из неравенства

≤ ( см. главу 2) Но мы не останавливаемся на нем.

Альтернативная формулировка: Пусть mnk=1; m,n,k>0, докажите что

≥ .

Задача 3:

Пусть a, b, c >0. Пусть , , . Докажите следующее неравенство: ≤ ; ≤ .

Замечание: Установим , мы придем к специальной формулировке:

≥ , когда d=10 и d= .

Для рассмотрения других симметричных полиномов ,

Cм. Болтянский В. Г. и Вигенских Н. Я. [4]

Задача 4:

Докажите что ≤ , где a, b, c>0.

Решение: из неравенства Коми- Шварца мы получаем

≥ ≥ . Используя их в нашем неравенстве, мы получаем:

≤ <=> ≤ <=>

<=> 3(ab+bc+ca)≤ <=> ≥0

Которое очевидно верно.

Примечание: Мы также можем решить его, трансформировав его в задачу 1(1).