§ 1.5 Шестиугольники и эллипсы.

В этом параграфе мы продолжим построение, которое рассматривалось в § 1.2, задача 1. Где А₁С₂||А₂С₁ , В₁А₂||В₂А₁ , В₁С₂|| В₂С₁ .

З адача 1. Докажите, что А₁ , А₂ , В₁ , В₂ , С₁ , С₂ лежат на эллипсе.

Решение: Противоположные стороны шестиугольника А₁С₂В₁А₂С₁В₂ параллельны, поэтому эти стороны пересекаются в 3 бесконечно удаленных точках, которые лежат на бесконечной прямой. По теореме Паскаля точки А₁ , А₂ , В₁ , В₂ , С₁ , С₂ лежат на эллипсе. Что и требовалось доказать.

рис. 1.22

Задача 2. Докажите, что все шесть сторон шестиугольника А₁А₂В₁В₂С₁С₂ (AZBXCY) касаются эллипса.

Решение: Основные диагонали этих шестиугольников конкуренты. Тогда по теореме Брианшона все стороны каждого шестиугольника А₁А₂В₁В₂С₁С₂ (AZBXCY) касаются эллипса. Что и требовалось доказать.

рис. 1.23

Задача 3. Доказать, что точки A , Z , B , X , C , Y лежат на эллипсе.

Решение: Известно, что для любых не коллинеарных 5-ти точек существует эллипс, проходящий через эти точки. Тогда существует единственный эллипс проходящий через точки B , Z, A , Y , C . Мы хотим доказать, что точка X так же на этом эллипсе. Мы доказали, что стороны шестиугольника А₁А₂В₁В₂С₁С₂ касаются эллипса. Тогда существует треугольник с вершиной в точке Z (описанные 2 вершины определяются автоматически это Y и X) который также описан и вписан в эти эллипсы. Поэтому точка Х лежит на эллипсе. Что и требовалось доказать.

Глава II – Геометрические неравенства.

В этой главе мы допускаем, что все условия задачи 1 в § 1.2. удовлетворены. Обозначим площади треугольников МС₁В₂ , МА₁С₂ , МВ₁А₂ , МА₁А₂ , МВ₁В₂ , МС₁С₂ , АС₁В₂ , ВА₁С₂ , СВ₁А₂ , за Т₁ , Т₂ , Т₃ , S₁ , S₂ , S₃ , Р₁ , Р₂ , Р₃ соответственно.

Первое неравенство:

Т₁ + Т₂ + Т₃ ≥ S₁ + S₂ + S₃

Доказательство: Чтобы доказать данное неравенство воспользуемся следующей леммой.

Лемма: T₂T₃ = S₁² , T₁T₃ = S₂² , T₁T₂ = S₃²

Д оказательство леммы: Из условия А₁С₂||А₂М ; А₁М||А₂В отсюда угол С₂А₁М = угол А₁МА₂ = угол МА₂В₁ = α . Пусть А₁С₂ = а, А₁М = в , А₂М = с , А₂В₁ = d . Найдём значение каждой площади T₂ , T₃ , S₁ и заменим их в равенство T₂T₃ = S₁² получаем ∙ = <=> ad = bc или a/c = b/d , а это равенство верно, т.к. ∆А₁С₂М~∆А₂В₁М и аналогично Т₁Т₃ = S₂² , Т₁Т₂ = S₃².

Доказательство первого неравенства:

T₁+T₂+T₃= + + ≥ + + =

= + +

И мы получили, что Т₁ + Т₂ + Т₃ ≥ S₁ + S₂ + S₃ .

Неравенство 2: Т₁ + Т₂ + Т₃ ≤ Р₁ + Р₂ + Р₃ .

Доказательство: Для начала докажем следующую лемму.

Лемма: , , .

Д оказательство леммы: Выразим стороны С₁М, МА₂ и С₂А₂ как a , b , c соответственно и пусть h высота ∆МА₁С₂ , которая равна так же высоте треугольников МС₁С₂ и МА₁А₂ из А₁С₂||А₂С₁ (рисунок 2.3). Тогда:

S₃ = , S₂= , S₁= , из подобия треугольников BA₁C₂ и BA₂C₁ следует, что:

= = = => = =>

=>

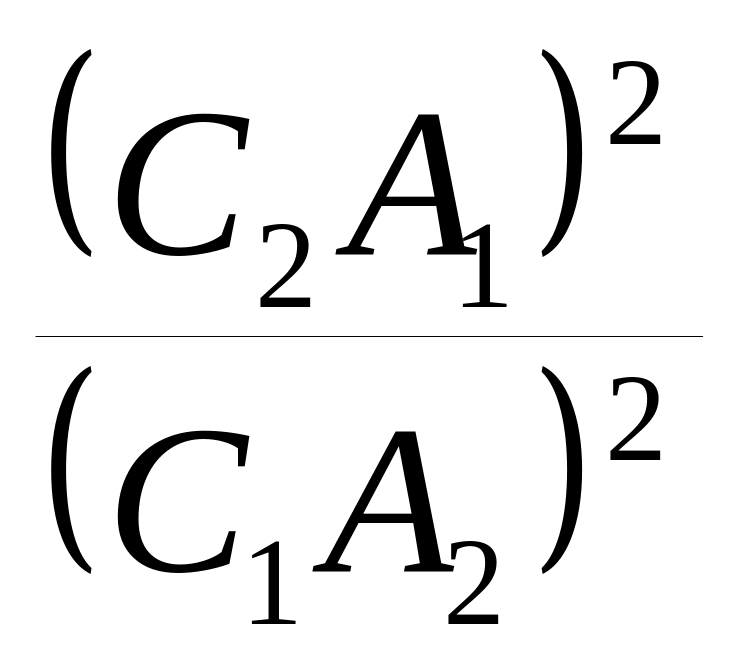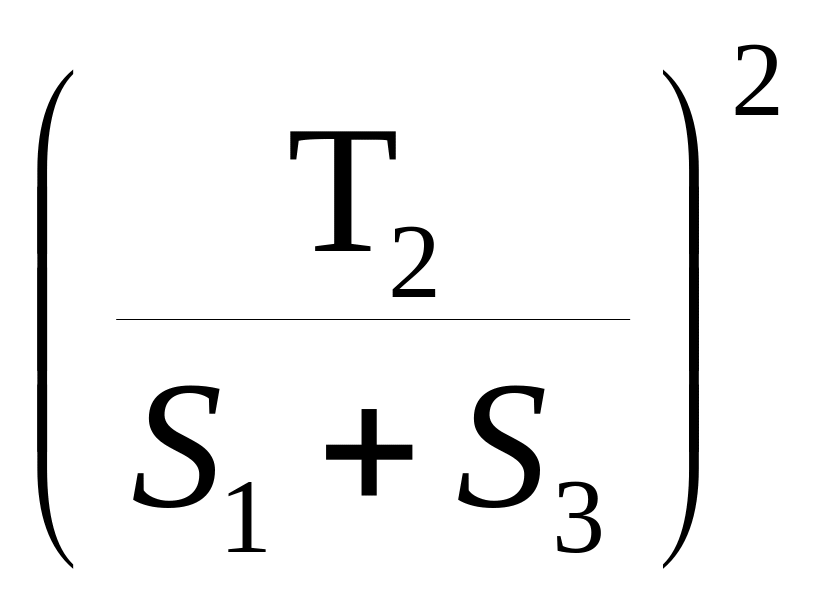Доказательство второго неравенства:

Заменяя P_i на полученную из Леммы формулы получаем

Т₁ + Т₂ + Т₃ ≤ + +

По неравенству Коши – Шварца:

+ + ≥ ≥

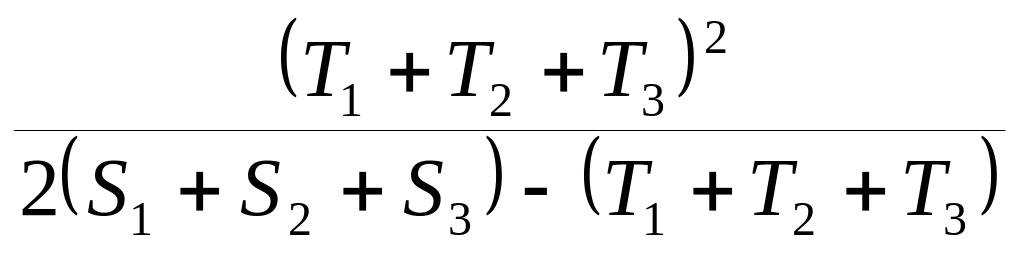≥ Т₁ + Т₂ + Т₃

Упростив последнее неравенство, мы получаем неравенство 1, которое уже доказано.

Неравенство 3: S₁ + S₂ + S₃ ≤ (A₀B₀C₀)

Доказательство: Очевидно, что площадь треугольника А₀В₀С₀ равна сумме площадей (MC’₁C₀C’₂) + (MB’₂C’₁) + (MB’₁B₀B’₂) + (MA’₂B’₁) + (MA’₁A₀A’₂) + (MA’₁C’₂) . Площадь параллелограмма MA’₁A₀A’₂ равна (MA₁A₂) , т.к. отрезки A’₁A’₂ , A₀B₀ , A₀C₀ делят треугольник МА₁А₂ на четыре равные части. Аналогично площади параллелограммов MB’₁B₀B’₂ и MC’₁C₀C’₂ равняются S₂ и S₃ соответственно. Аналогично мы получаем, что площади треугольников MB’₂C’₁ , MA’₂B’₁ , A’₁C’₂ равны площадям треугольников (МС₁В₂) , (МВ₁А₂) , (МА₁С₂) соответственно. Из этого следует что

= + + + + + = (S₁ + S₂ + S₃) + .

Теперь неравенство 3 обретает следующий вид:

≤,

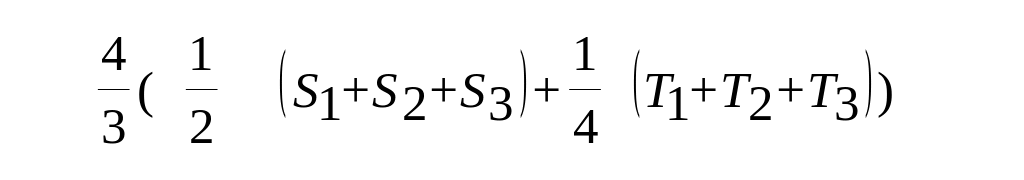
упростив последнее неравенство, получим S₁ + S₂ + S₃ ≤ T₁ + T₂ + T₃ , которое уже доказано.

Неравенство 4: ≤

Доказательство:

Мы докажем неравенство используя формулу для вычисления площади

треугольника из последнего неравенства. Площадь шестиугольника

равна сумме площадей следующих треугольников

. Тогда мы имеем следующее,

≤ =>

=> ≤ =>

=> ≤

Теперь мы получаем, что ≤ .

Неравенство 5: ≤

Мы используем следующую формулу: =

Заменяя её в неравенстве, мы получаем, что

≤ . Упростив это выражение, мы получаем первое неравенство: ≥ .

Равенство1: =

Доказательство: из C₂A₁||CA следует что (MC₂A₂)= (MA₁A₂)= S₁, аналогично (MA₂B₂)= (MB₂B₁)= S₂ и (MC₂B₂)= (MC₂C₁)= S₃. Тогда

=(MA₂B₂)+(MC₂B₂)+ (MC₂A₂)= S₁ + S₂ + S₃

А налогично = S₁ + S₂ + S₃ следует что равенство = верное.

Неравенство 6: ≤

Доказательство: ≤

Заметим из доказательства 2-го неравенства имеем, что и т.д. поэтому неравенство имеет следующий вид:

2 ≤ + +

Ещё раз используем неравенства Коши-Шварца:

+ + ≥

Пусть = a и = b (Заметим, что 2a>b что следует из формулы площади для P_i) наше неравенство становится:

разложив на множители: что верно из

Неравенство7: ≤ Р₁ + Р₂ + Р_3.

Доказательство: Площадь = + Р₁ + Р₂ + Р₃+

Заменим это в нашем неравенстве 7 и упростив получим:2 (Р₁ + Р₂ + Р₃) ≥ ≥ + . Ещё раз используем формулу и т.д. получаем: 2( + + ) ≥ +

Заметим, что по Коши-Шварца

≤ + +

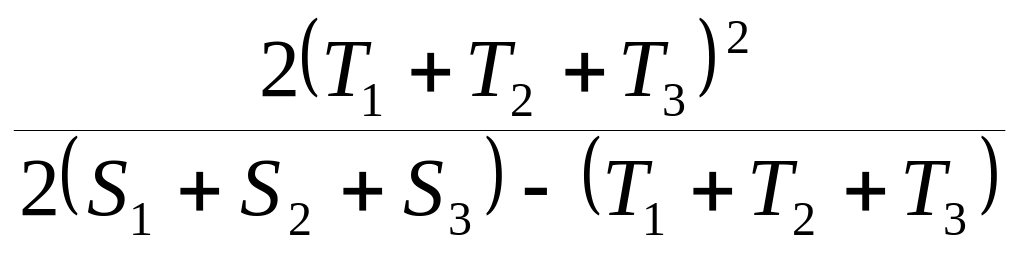Остаётся доказать, что

≥ +

Воспользуемся заменой, которую использовали в доказательстве 6-го неравенства, получаем, что ≥ <=> ≥ <=> ≥ или ≥ 0 что верно, так как ≥ ≥0.

Равенство 2: <S (XYZ) = 4(A₀B₀C₀)

Доказательство: треугольники XYZ и A₀B₀C₀ гомотетичны с коэффициентом гомотетии равным 2 . Поэтому

площадь треугольника XYZ больше площади A₀B₀C₀ в 4 раза

Неравенство 8: ≥

Доказательство: мы уже доказали, что

T₂T₃ = S²₁ , T₁T₃ = S₂² , T₁T₂ = S₃²

Тогда используя эти равенства, получаем, что

≥

+ + ≥ 0.

Что верно, так как квадрат числа всегда положителен.

Неравенство 9 ≤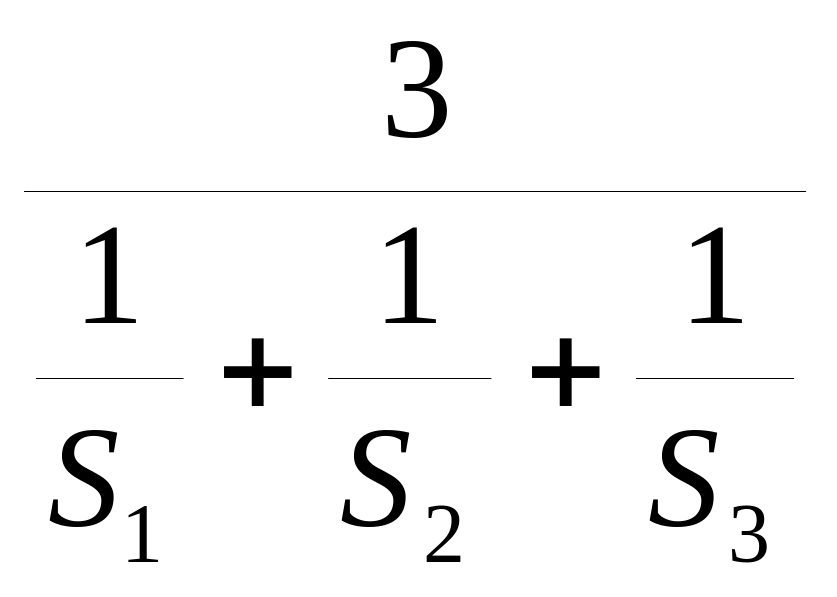

что можно доказать через среднее гармоническое, среднее арифметическое. Но мы можем получить это неравенство, суммировав все наши неравенства в одну цепочку.

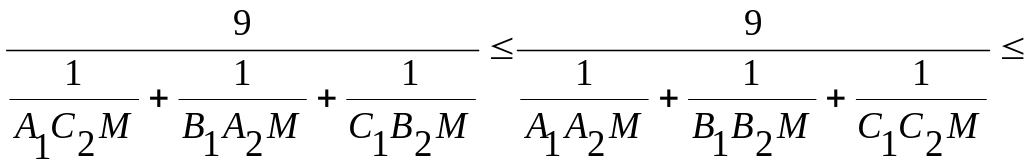
Теперь мы покажем другой метод решения этого неравенства. Это более стандартный метод решения так называемых «Афинских» задач.

Например докажем такое неравенство :

≥

Доказательство : Мы обозначим площади треугольников BMC, CMA, AMB за Q₁, Q₂, Q₃ . (рис.19). Очевидно, что , , .

Тогда и .

.Тогда =

= . Так как , тогда из подобия треугольников и

мы получаем, что

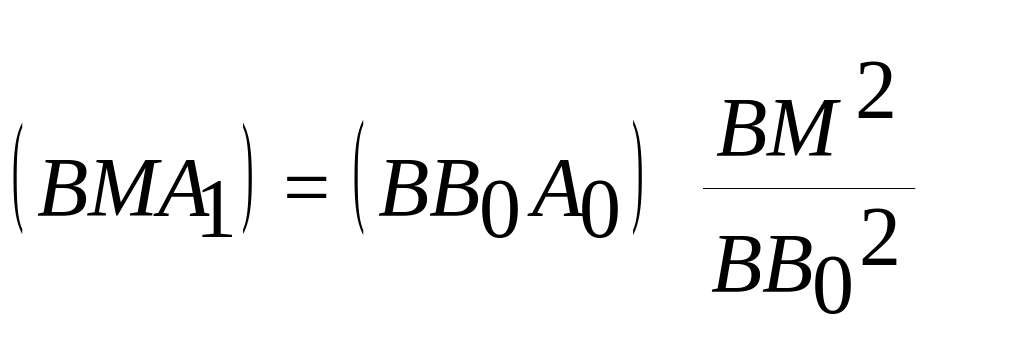= . Аналогично

. Тогда

- - = . Аналогично

= , = .

Мы получаем что:

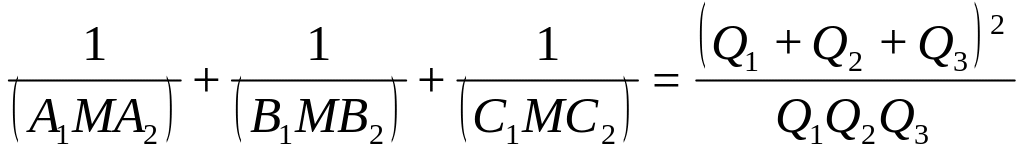≥ , так как ≥27

Равенство достигается при . То есть когда точка М центр масс треугольника ABC.

Примечание: Мы можем выразить площади других треугольников через Q₁, Q₂, Q_3. Мы попытались доказать неравенства по цепочке используя эти формулы. Это навело нас на новый вид алгебраических неравенств которые мы рассмотрели в третьей главе.