Сравнение моделей.

Наиболее распространенными критериями для определения наилучшей модели в случае, когда не известна верная спецификация, являются критерий Шварца (Schwarz) и критерий Акайке (Akaike). Также дополнительно рассчитаем критерий Ханнана-Куина. Эти три критерия позволяют выбирать наилучшую модель из множества различных спецификаций. Критерии численно построены так, чтобы учесть влияние на качество подгонки модели двух противоположных тенденций.

Критерий Акаике вычисляется по следующей формуле:

Критерий Шварца:

Критерий Ханнана-Куина:

, где k – число параметров модели, n – число наблюдений, ln L – максимизированное значение функции правдоподобия модели. Наилучшей модели соответствуют наименьшие значения критериев. Сведем результаты вычислений в таблицу:

Таблица 6 Сравнение информационных критериев моделей бинарного выбора.

Как видно из таблицы выше - gompit-модель является наилучшей. Все параметры почти на 0,025 ниже, чем у logit-модели и на 0,022 меньше, чем у probit-модели.

Изобразим наглядно предельные эффекты всех моделей на одном графике:

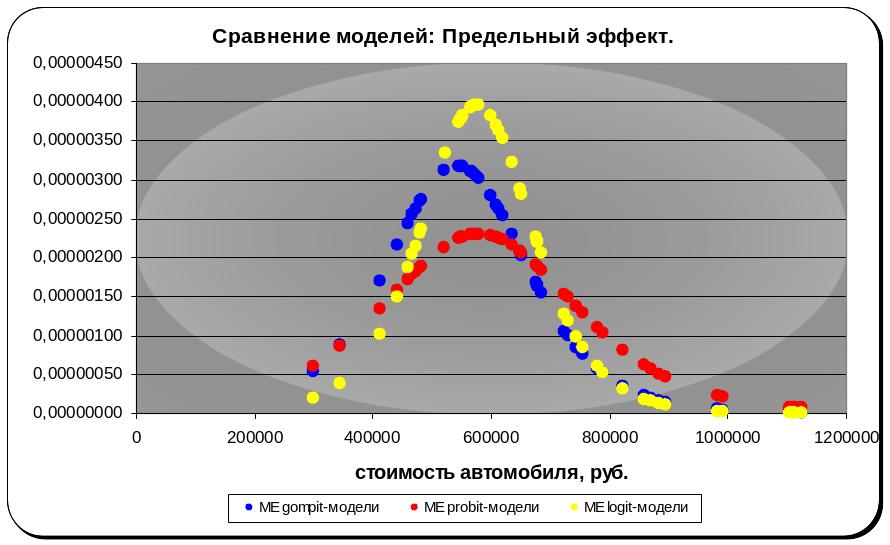
Рисунок 8 Сравнение предельных эффектов моделей бинарного выбора.

Как видно из графика выше, Y во всех трех моделях наиболее чувствителен при средних значениях цены автомобиля. Как видим, наибольшую чувствительность х к y показывает logit-модель, а наименьшую – probit. Предельные эффекты gompit-модели находятся между предельными эффектами двух других моделей для средних значений стоимости автомобиля.

Модели множественного выбора

В случае, если результирующая переменная принимает более, чем 2 дискретных значения, используются модели множественного выбора:

• Модели, построенные на основе моделей бинарного выбора - logit, probit и gompit;

То есть исследуется модель с упорядоченным откликом.

• Модель целочисленных значений – если данные распределены по закону Пуассона.

Рассмотрим другую задачу с содержательной точки зрения: посмотрим, как стоимость страховки влияет на наступление страхового случая (0, 1 и 2 раза). Предполагается, что стоимость полиса влияет на стиль вождения и поведение на дороге. Так, предполагается, что особо дорогой полис может снизить бдительность водителя из-за уверенности в быстрой компенсации или способности отремонтировать транспортное средство самому (косвенное влияние франшизы). Покупатель более дешевой страховки, наоборот, может относиться к классу малоимущих граждан и приобретает полис с целью обезопасить автомобиль, соответственно ездит аккуратно. Однако, данные предположения (помимо всего прочего) зависят от социально-психологической составляющей, поэтому выборку из 50 автомобилей, проведенных ранее, расширим до 1000.

Таким образом, исходные данные представимы в следующем виде:

Рисунок 9 Диаграмма разброса принятия решения о количестве покупаемых автомобилей в зависимости от цены КАСКО первого автомобиля.

Под «0» имеется ввиду, что для данного автомобиля не было зарегистрировано ни одного страхового случая. «1» - 1 страховой случай, а «2» страховых случая, зарегистрированных на одно и то же транспортное средство.

Как уже упоминалось выше, существуют несколько моделей множественного выбора. Сперва, остановимся поподробнее на моделях, в основе которых лежат logit, probit и gompit оценивание.

Оценки модели, полученные Методом Максимального Правдоподобия для probit – модели, сведены в следующую таблицу:

Таблица 7 Результат построения ММП оценок.

Все коэффициенты значимы, как и вся модель в целом, т.к.

LR-статистика =-2(lnL₀-lnL₁) =665, 246 превышает критическое значение.

Вычислим характеристики правдоподобия: Логарифм правдоподобия равен: , а

. Рассчитаем показатели качества модели: ;

. Если проводить аналогию с коэффициентом детерминации, то модель объясняется 34% дисперсии. Это не совсем корректно, однако помогает лучше воспринимать оценку качества.

Прогнозные значения y рассчитывались следующим образом: если значение линейной комбинации регрессоров было меньше первой границы, то y присваивалось значение 0, если оно попадало в интервал между двумя границами – 1, в остальных случаях – 2. Вероятности принадлежности к классам при этом рассчитываются по формулам:

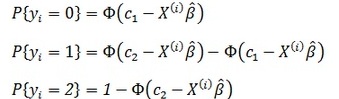
Графически это можно изобразить следующим способом:

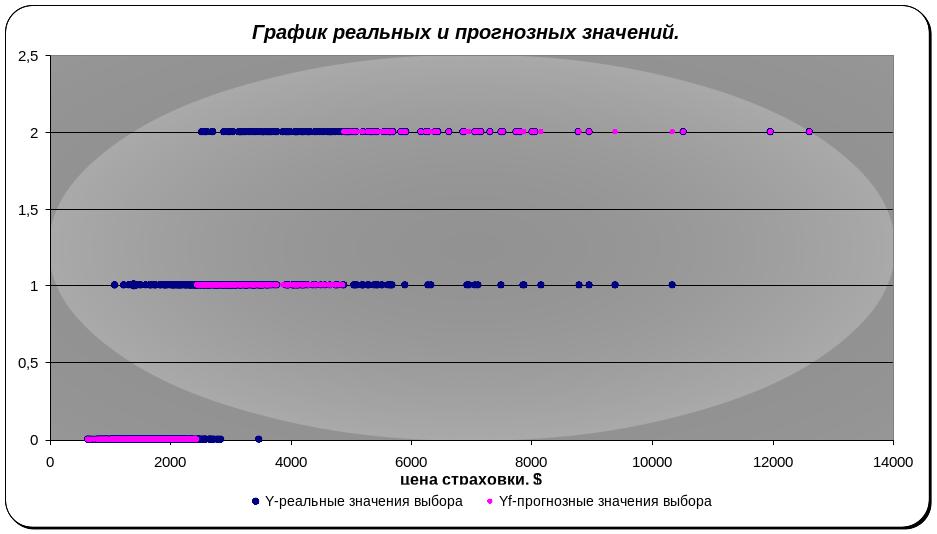
Рисунок 10 Диаграмма разброса реальных прогнозных решений о покупке автомобиля в зависимости от цены страховки.

С помощью графического анализа сразу можно заметить, что весомая доля наблюдений классифицирована не верно, то есть неправильно предсказывает значения для большего числа наблюдений.

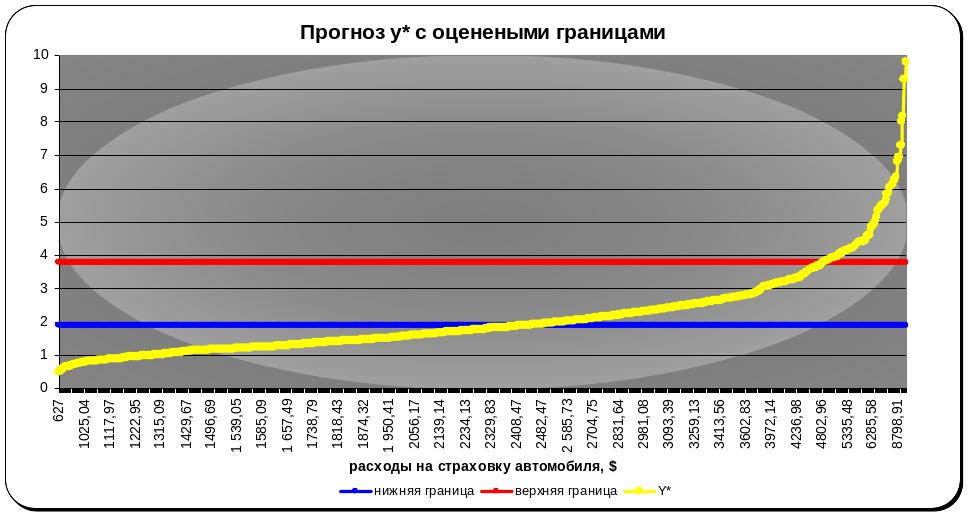
Рисунок 11 График прогнозных значений зависимой переменной.

Изобразим наглядно значения вероятности:

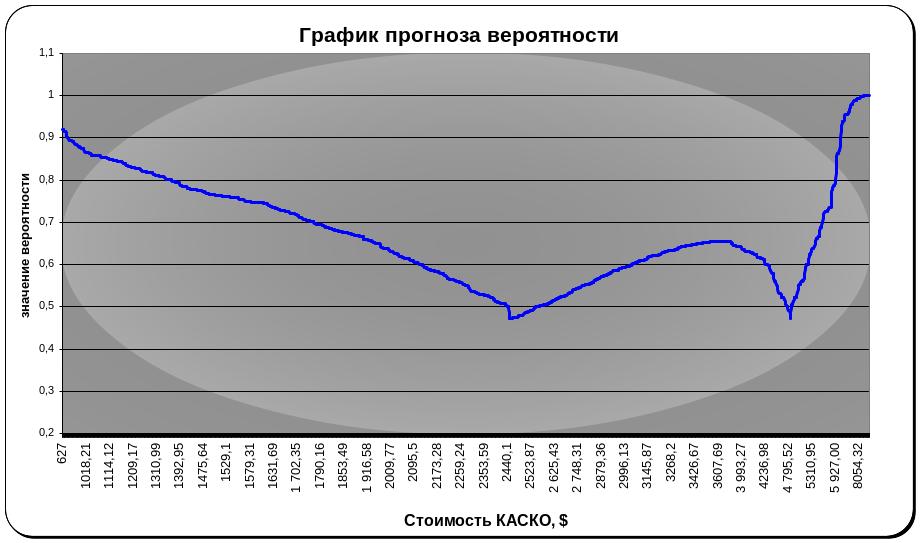
Рисунок 12 График прогноза вероятности.

Видно, что велика вероятность попасть в аварию для наблюдений с самыми низкими ценами страховки, однако она существенно снижается при подходе к границе С1.Для среднего класса самая высокая вероятность не в середине класса, а смещена вправо (ближе к 3му классу). Понижение слева и справа соответствует переходу в соседние классы. Для третьего класса вероятность в нем остаться повышается с ростом стоимости страхового полиса.

Рассмотрим так же график предельных эффектов:

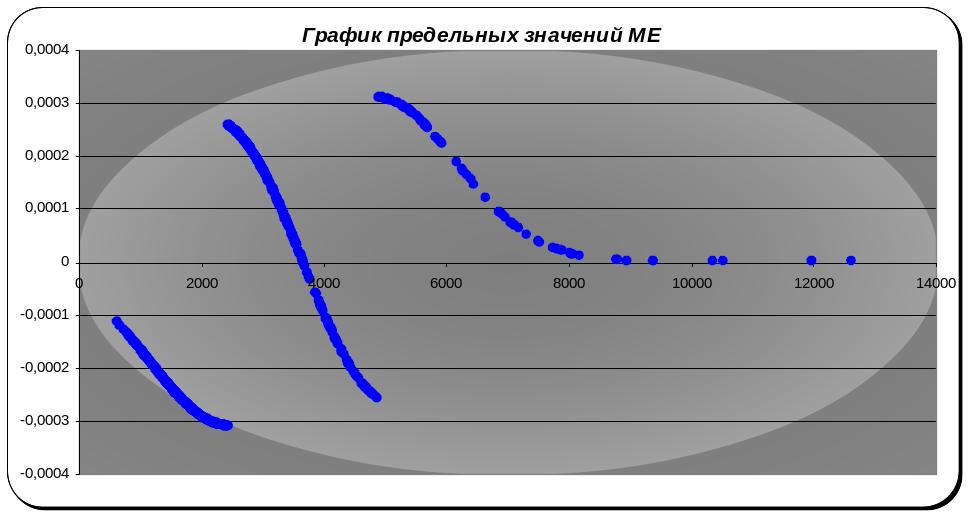
Рисунок 13 График предельных значений.

Отрицательные значения для первого класса означают снижение вероятности остаться в классе при увеличении стоимости полиса. Для среднего класса прирост вероятности перехода в соседние классы симметричен относительно центра класса. Для третьего класса прирост вероятности остаться в нем положителен, но стремиться к 0 для очень высоких значений стоимости КАСКО.

Другие модели множественно го выбора: логит и гимпит.

Таблица 8 Результат построения логит-модели

Таблица 9 Результат построения gompit-модели

Все коэффициенты значимы и в гомпит и в логит моделях, сами модели так же значимы (значение наблюдаемых LR статистик превосходит критические).

Теперь определим долю наблюдений, для которых исходные и модельные значения зависимой переменной совпали и не совпали.

Таблица 10 Сравнение моделей множественного выбора по доле верно определенных значений

Из таблицы 10 видно, что пробит-модель обладает более высокой долей верно классифицированных объектов (75,1%). Количество правильно определенных наблюдений в пробит-модели на 51 больше, чем в логит модели и на 27 больше, чем в гомпит-модели.

Проведем сравнительный анализ на основе информационных критериев:

Таблица 11 Сравнение информационных критериев

Как видно из таблицы выше наилучшей моделью так же является probit-модель. Все параметры почти на 0,021 ниже, чем у logit-модели и на 0,012 меньше, чем у gompit-модели. Следует отметить, что гипотеза о нормальности распределения остатков в этой модели принимается на уровне значимости 5% в соответствии с критерием Жарке-Бера (т.к JB=2,01 < Х²_крит =5,99) . Распределение остатков представлено на рисунке 12.

Таблица 12 Гистограмма распределения остатков probit-модели.

Также в модели отсутствует автокорреляция (вплоть до 3его порядка). Данный вывод был получен на основе теста Бокса-Пирса (наблюдаемое значение статистики меньше критического). Автокорреляция чаще всего проявляется во временных рядах. Выборка, используемая для данного анализа – одномоментная.

Таблица 13 Результат проведения теста Бокса-Пирса на автокорреляцию до 3-ого порядка.

Проверка остатков на гетероскедастичность с помощью Теста Уайта дала следующие результаты. Наблюдаемое значение статистики Х² равняется 68,7268 , тогда как X²кр=5,99 , следовательно, гипотеза о гомоскедостичности отвергается с вероятностью ошибки 0,05. Такой вид нарушений стандартных предположений, как неоднородность дисперсий ошибок, характерен для статистических данных, относящихся к одному моменту времени, но собранных по разным регионам, предприятиям, и т.д.