Национальный исследовательский университет
Высшая школа экономики
Отделение статистики, анализа данных и демографии факультета экономики
Отчет № 2 предмету эконометрика на тему:
«Изучение стоимости полиса автострахования КАСКО»
Выполнила: Беднарская К.П.
Студентка группы С31
Москва,
2012 г.
Оглавление:
Оглавление: 2
Модели с дискретными зависимыми переменными 3
Logit-модель. 4
Probit-модель 6
Gompit-модель. 8
Модели множественного выбора 12
Модели с дискретно-непрерывными переменными 21
Модель с цензурированными выборками 21
Модель с урезанными выборками 23
Модель Хекмана. 27
Модели с дискретными зависимыми переменными Модели бинарного выбора.
В Данной главе будем исследовать влияние
стоимости автомобиля на наличие
страховки. Существуют только две
альтернативы для автовладельца: покупать
или не покупать полис автострахования
КАСКО. То есть будем анализировать
бинарную зависимую переменную, которая
имеет значения 0 (отрицательное решение)
и 1 (положительное решение). Для анализа
произведена случайная выборка из 50
объектов. Графически это можно представить
следующим образом:
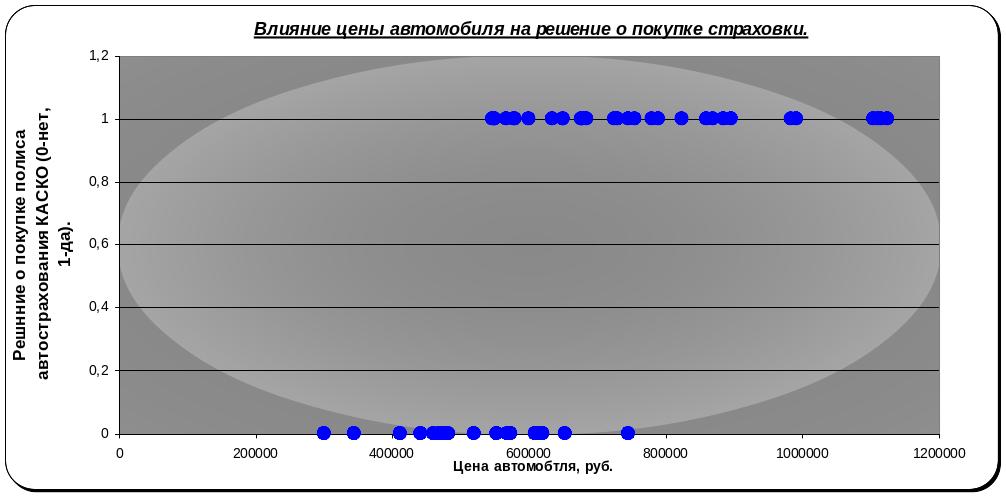
Рисунок 1 График зависимости решения о покупке страховки от расходов на автомобиль.
Сохраняя основные идеи регрессионного подхода, будем предполагать, что на решение автовладельца так же влияют неучтенные случайные факторы (ошибки). Выдвигая различные предположения о характере зависимости между переменными хi и у, будем получать разные модели, а именно: logit-, probit-, gompit-модели, после оценивания которых определим наилучшую.
Logit-модель.
Данная модель предполагает логистическое распределение функции вероятности события, то есть вероятность успеха (приобретения страховки) определяется функцией:
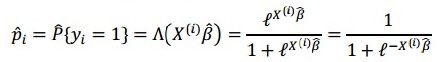
где (Xi) – линейная комбинация объясняющих переменных/
Если для р получится значение меньшее 0,5, то можно предположить, что событие не наступит – владелец автомобиля откажется от покупки страховки, в противном случае предполагается наступление события – приобретение полиса.
Изобразим рассчитанные значения вероятности на графике:
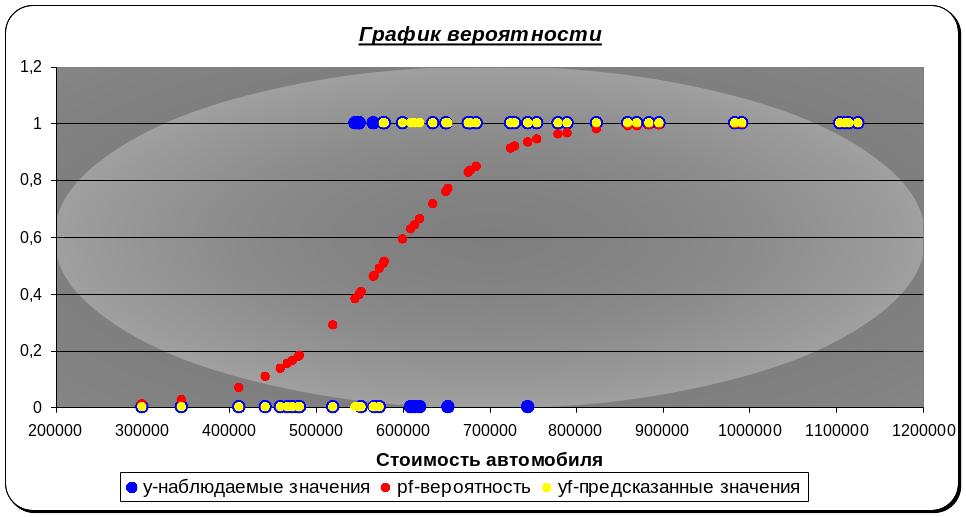
Рисунок 2 График вероятности
Из представленного графика видно, что всего 8 наблюдений классифицировано не верно.
Оценив параметры модели методом максимального правдоподобия , получим значения, представленные в следующей таблице:
Таблица 1 Результат построения логистической регрессии.
Коэффициент b0 в данном случае не имеет экономической интерпритации. Положительный коэффициент регрессии свидетельствуют о положительном влиянии цены автомобиля на решение о страховании.
Определим значимость модели. Для этого вычислим статистику LR, используя следующую формулу: LR=-2(lnL0 – lnL1), где ln L0 :
,
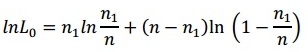а Ln l1-
логистическое правдоподобие:
Значение LR статистики (27,3) превосходит критическое значение, на основе чего можно сделать вывод о значимости всей модели. Отметим так же, что все коэффициенты регрессии так же значимы.
При оценивании методом максимального правдоподобия не существует меры качества оценивания, аналогичной коэффициенту R2.В этой ситуации для сравнения альтернативных спецификаций моделей были предложены другие многочисленные меры:
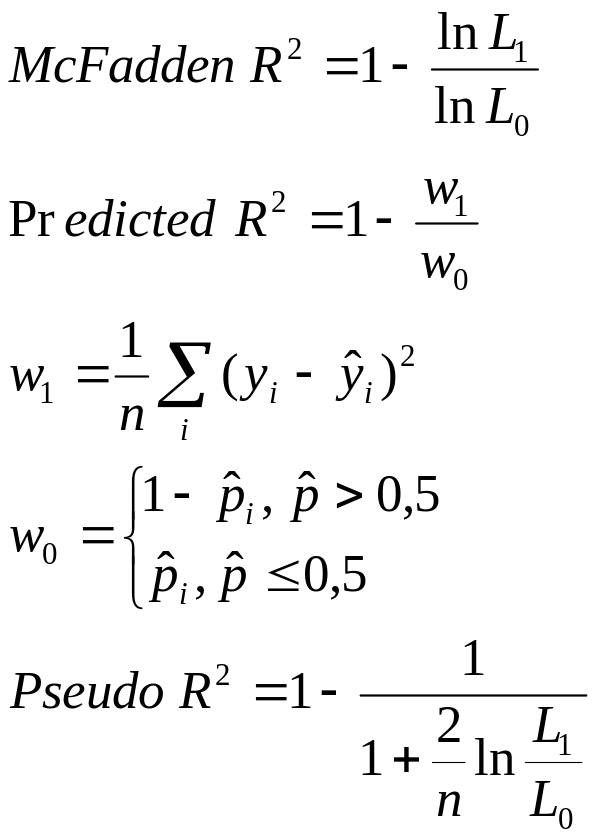
Каждая из этих мер имеет свои недостатки, поэтому для более корректных выводов рекомендуется рассчитывать несколько коэффициентов.
Таблица 2 Коэффициенты детерминации логистической регрессии.
В общем виде представить воздействие
стоимости автомобиля на решение о
покупке страхового полиса можно с
помощью предельного эффекта. Посчитаем
предельный эффект коэффициента :
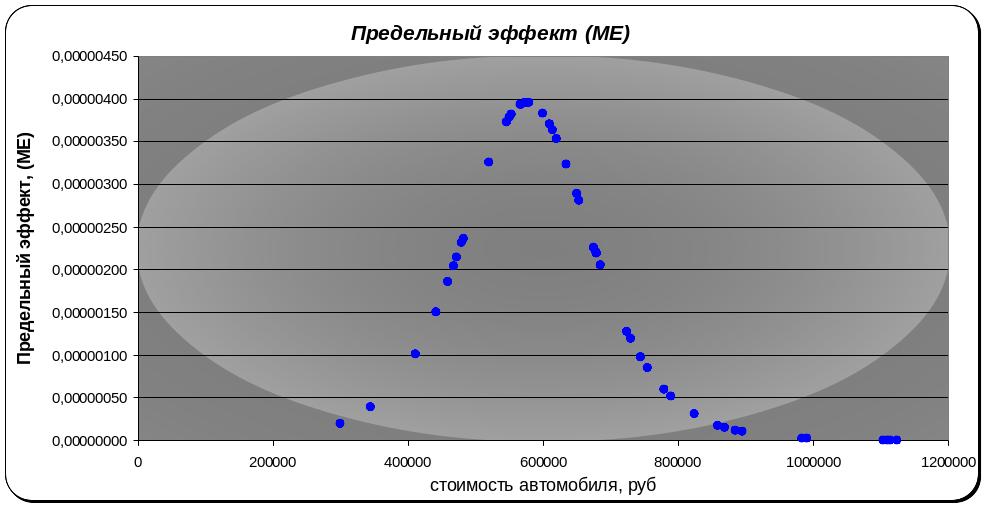
Рисунок 3 График влияния предельного эффекта на вероятность.
Из графика, представленного выше, видно, что для средних значений цены автомобиля прирост вероятности единичного значения больше, чем для крайних значений. Чувствительность вероятности наиболее велика в центральной точке.