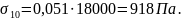Задание 2.3

Построить эпюру распределения напряжений от сосредоточенной силы с шагом 1 и до глубины 10 м.

а) Под точкой приложения силы

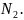
Вертикальные напряжения в точке М определяют по формуле:

k – безразмерный коэффициент, зависящий от соотношения r/z;

N – величина вертикальной силы;

z, r – соответственно вертикальная и горизонтальная координаты точки М.

В точке М₀

в точке М₁

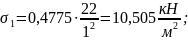
в точке М₂

в точке М₃

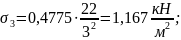
в точке М₄

в точке М₅

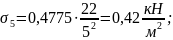
в точке М₆

в точке М₇

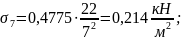
в точке М₈

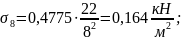
в точке М₉

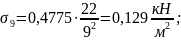
в точке М₁₀

Для построения эпюры примем масштаб 1см = 1 .

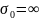
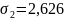
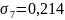
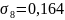
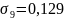
б) на расстоянии от точки приложения силы .

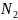В точке М₀

в точке М₁

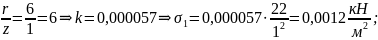
в точке М₂

в точке М₃

в точке М₄

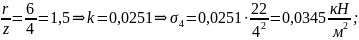
в точке М₅

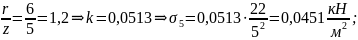
в точке М₆

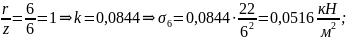
в точке М₇

в точке М₈

в точке М₉

в точке М₁₀

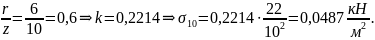
Д

ля построения эпюры примем масштаб 1см = 0,01 .

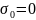
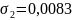
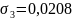
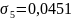
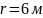
Задание 2.4

Определить напряжение в точке М, находящейся на глубине z₃ = 3,2 м под центром прямоугольной равномерно распределённой нагрузки интенсивностью p₁ = 11 кПа, приложенной к поверхности грунтового основания. Размеры фундамента b₁ = 2 м и l₁ = 3,6 м.

Решение:

l₁ = 3,6 м

p = 11 кПа

b₁ = 2 м

z₃ = 3,2 м

M

Находим соотношения

По таблице для значений находим коэффициент

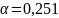и вычисляем напряжение по формуле:

Задание 2.8

С шагом z = 0,8 м до глубины 8 м определить вертикальные напряжения от загружения под центром прямоугольной равномерно распределённой нагрузки интенсивностью p₃ = 18 кПа, приложенной к поверхности грунтового основания. Размеры фундамента Ф равны b₁ = 2 м и l₁ = 3,6 м.

Р

l₁ = 3,6 м

ешение:

p = 18 кПа

b₁ = 2 м

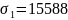
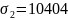
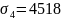
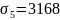
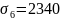
z₃ = 0,8 × 10 = 8 м

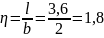– общая для всех точек.

Для М₁

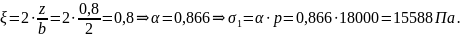
Для М₂

Для М₃

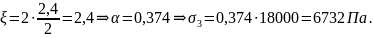
Для М₄

Для М₅

Для М₆

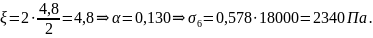
Для М₇

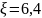Для М₈ . Для ближайшие значения коэффициента 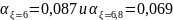, разность между ними ∆ ′ = 0,087 – 0,069 = 0,018, разность соседних значений ∆ = 6,8 – 6,0 = 0,8. Приращение значений ∆′ , соответствующее значению , равно ∆′ = 6,8 – 6,4 = 0,4. Составим пропорцию, обозначая искомое приращение коэффициента через ∆ .

откуда ∆ = 0,069 + 0,009 = 0,078

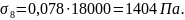
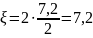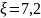Для М₉ . Для ближайшие значения коэффициента , разность между ними ∆ ′ = 0,069 – 0,056 = 0,013, разность соседних значений ∆ = 7,6 – 6,8 = 0,8. Приращение значений ∆′ , соответствующее значению , равно ∆′ = 7,6 – 7,2 = 0,4. Составим пропорцию, обозначая искомое приращение коэффициента через ∆ .

откуда ∆ = 0,056 + 0,0065 = 0,0625

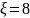Для М₁₀ . Для ближайшие значения коэффициента , разность между ними ∆ ′ = 0,056 – 0,046 = 0,01, разность соседних значений ∆ = 8,4 – 7,6 = 0,8. Приращение значений ∆′ , соответствующее значению , равно ∆′ = 8,4 – 8 = 0,4. Составим пропорцию, обозначая искомое приращение коэффициента через ∆ .

откуда ∆ = 0,046 + 0,005 = 0,051