2. Представление пространства поиска.

Множество всех дискретных состояний образует дискретное пространство состояний (далее просто пространство состояний): S = {s1, s2, …, s_m}, где m количество всех состояний множества S. Всякое состояние si из S характеризуется множеством признаков K = {k1, k2, …, k_n}.

1)подмножество родовых признаков состояний K^R ⊆K,

2)подмножество видовых признаков состояний K^V ⊆ K.

Пространство состояний можно охарактеризовать отношением «часть – целое»:

где Si подмножества множества S.

Причем должно быть выполнено условие

Отношение «часть – целое» обуславливает то, что пространство состояний включает в свой состав:

1) подмножество S_o начальных состояний

2) подмножество S_t целевых состояний.

3) подмножество S_с текущих состояний.

Важным понятием, используемым при решении задач в пространстве состояний, является понятие пространство поиска S^R. Необходимость введения понятия S^R продиктовано, прежде всего, возможными ситуациями, когда пространство состояний состоит из нескольких несвязных подпространств состояний, каждое из которых представляет собственное пространство поиска.

В отличие от пространства состояний для пространства поиска выполняется следующее условие. Для любой пары состояний (si, sj) ∈ S^R всегда найдется одна и более цепочек операторов Li = (f1, f2, …, fn), применение которой к состоянию si приведет к состоянию sj. Причем все текущие состояния, представляющие некоторый путь от состояния s_i до состояния _sj, также будут принадлежать данному пространству S^R. Следовательно, множество S^R – это всегда связная область.

Между пространством состояний и пространством поиска существуют следующие отношения: S ⊇ S^R и

|S | ≥ |S^R|. Пространство поиска в составе пространства состояний образуется за счет дальнейшего обобщения видовых признаков некоторых состояний.

Организацию состояний можно отобразить с помощь матриц смежности и инцидентности. Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг некоторой вершины x_iG:

[a_ij] x_i,y_j = [n * m],

где a_ij – отношение инцидентности дуги y_j к вершине x_i орграфа G, n – количество строк вершин орграфа, m - количество столбцов дуг орграфа.

Отношение a_ij обозначается «1», если дуга y_j выходит из вершины x_i, иначе «0» (если дуга y_j входит в вершину x_i).

Видовые признаки:

1. расположение вершин в пространстве,

2. порядок,

Родовые признаки:

1. цифры,

2. количество цифр(4 цифры),

3. количество расположений вершин.

	1234	2314	2431	4321	4132	4213	1423	3412	1342	3124	3241	2143
1234	0	1	0	0	0	0	1	0	1	1	0	1
2314	1	0	1	0	0	0	0	0	0	1	1	1
2431	0	1	0	1	0	1	0	0	0	0	1	1
4321	0	0	1	0	1	1	0	1	0	0	1	0
4132	0	0	0	1	0	1	1	1	1	0	0	0
4213	0	0	1	1	1	0	1	0	0	0	0	1
1423	1	0	0	0	1	1	0	0	1	0	0	1
3412	0	0	0	1	1	0	0	0	1	1	1	0
1342	1	0	0	0	1	0	1	1	0	1	0	0
3124	1	1	0	0	0	0	0	1	1	0	1	0
3241	0	1	1	1	0	0	0	1	0	1	0	0
2143	1	1	1	0	0	1	1	0	0	0	0	0

Анализ матрицы смежности для прямого правила:

Матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей. Матрица состоит из совокупности матриц для орграфов «Дерево» и «Кольцо».

Орграф состоит из множества колец. Каждое кольцо содержит три вершины. Из каждой вершины выходит три кольца. Отсутствуют корневые и терминальные вершины. Каждая вершина имеет равное количество входящих и исходящих вершин (три входящих и три исходящих). Одна из связей дублирует сама себя – то есть из одной вершины x_i направлена связь к другой x_i+1, из которой в свою очередь тоже направлена связь на эту вершину x_i.

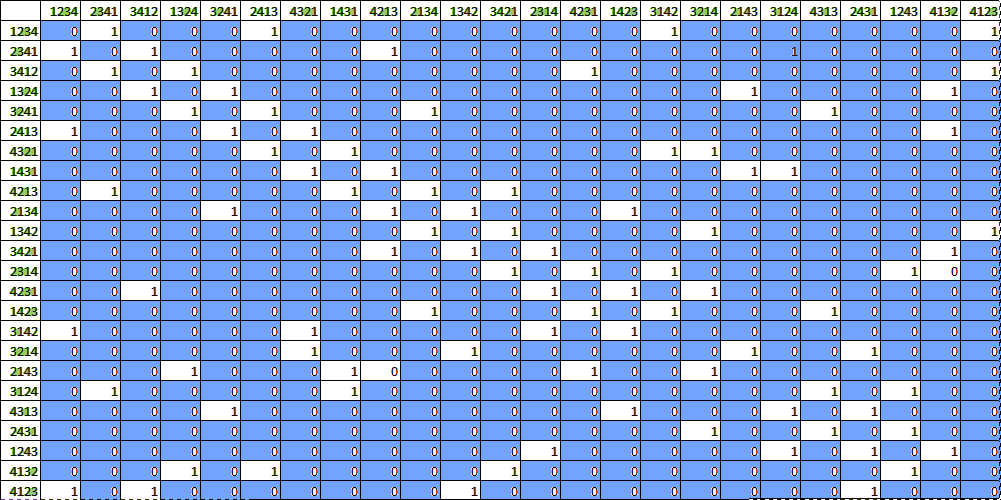
Анализ матрицы смежности для обратного правила:

Матрица симметрична относительно главной диагонали, а главная диагональ состоит из нулей. Матрица состоит из совокупности матриц для орграфов «Дерево» и «Кольцо».

Отсутствуют корневые и терминальные вершины. Каждая вершина имеет равное количество входящих и исходящих вершин (три входящих и три исходящих). Две связи дублируют самих себя. Внутри орграфа имеются прямоугольные плоскости.

Между состояниями пространства поиска существует отношение «род-вид»:

Родовые признаки:

1. Элементы пространства состояний – цифры.

2. Равное количество цифр – числа четырехзначные.

3. Нет корневых и терминальных вершин.

4. Количество связей (шесть связей). Выходит 3 связи (n-1) и 3 связи входят (n-1).

5. У каждой вершины есть хотя бы одна связь, которая повторяется.

6. Если поменять местами соседние цифры в вершине – то вершина станет принадлежать другому подпространству.

Видовые признаки:

1. Правила перебора (прямое правило, обратное правило).

2. Количество вершин.

3. Расположение в пространстве.

4. Без повторяющихся связей орграф, образованный прямым правилом, имеет пять связей, а орграф, образованный обратным правилом – четыре связи.

Между состояниями пространства поиска существует отношение «часть-целое», так как имеется подмножество начальных состояний, из которых начинается поиск, подмножество целевых состояний, где поиск заканчивается, и подмножество текущих состояний, которое является промежуточным звеном.

Вывод:

Всякое состояние характеризуется множеством родовых и видовых признаков.

Представление пространства состояний в виде орграфа G = (X{xi},Y{yj}) позволяет выделить дополнительные свойства и организацию состояний:

1) если |Yin{yj}| = 1 и |Yout{yj}| = 1, то орграф представляет собой

кольцо;

2) если |Yin{yj}| = и |Yout{yj}| = , то граф является несвязным;

3) если |Yin{yj}| = 1 и |Yout{yj}|≠ 1, то орграф представляет собой

расходящееся от корня дерево;

4) если |Yin{yj}| ≠1 и |Yout{yj}| = 1, то орграф представляет собой

сходящееся к корню дерево;

5) если |Yin{yj}|≠ 1 и Yout{yj}= , то вершина является терминальной;

6) если |Yin{yj}| = и |Yout{yj}| ≠ 1, то вершина является корневой.

Матрица смежности позволяет представить бинарные отношения между вершинами орграфа.

Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг вершин орграфа.